Discriminative Training for Language Models

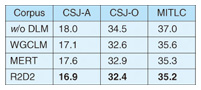
1. Introduction

Recent advances in natural language processing technology have led to the development of many convenient applications, which not only enable us to communicate with computers in a human-like manner using natural language but also aid our conversation, work, and thinking. They include automatic speech recognition (ASR), machine translation, information retrieval from texts, dialogue systems, and applications combining them.

One of the key techniques for achieving these applications is language modeling. Language models (LMs) are basically used to measure the appropriateness of a sentence as natural language. For example, they can be used to choose the best sentence from multiple sentences by measuring their appropriateness. While many kinds of LMs exist, back-off n-gram modeling is one of the most basic and important techniques. This technique is very simple and its model is powerful despite being easily obtained by counting the number of occurrences of each n-gram (an n-tuple of consecutive words) in training data.

Other LM techniques measure the appropriateness of a sentence taking account of factors such as syntax, the dependencies between words and topics. They commonly train a model by estimating distributions of words and symbols of syntax. In short, these techniques generate a model that gives a high score to high-frequency words, as with back-off n-gram LM techniques. However, when an LM is used for ranking sentences or estimating the class of a sentence, it should be trained so that reference sentences are distinguished from the other sentences. For example, in the case of ASR, reference sentences should be distinguished from the other possibly misrecognized sentences. As a method that meets this requirement, discriminative training has been attracting increasing attention in the natural language processing community [1]–[4]. In the discriminative training framework for ASR, speeches in a training set are recognized by using a speech recognizer. Then, the sentences of the recognition result, together with their reference sentences, are used for training the language model. The model is trained so that the references are distinguished from the misrecognized sentences [5], [6].

Discriminative language models (DLMs) are effective, but problems to be solved remain. This article mentions two problems with DLMs. The first is that the best learning machine for DLM training depends on datasets even with the same task (application) [7]. This requires a DLM specialist to carefully choose a learning machine before training starts. A novel learning machine to overcome this problem [8] is described in section 3.1, which also describes its relationship to and advantages over conventional learning machines. Experimental ASR results that reveal the effectiveness of the novel learning machine are presented in section 4.

The other problem relates to the number of parameters. DLM training requires improper (possibly misrecognized) sentences and proper reference sentences and then obtains features from both types of sentence, whereas conventional back-off n-gram LMs obtain features from only reference sentences. Hence, DLMs tend to have a much larger number of features, which means they have more parameters than conventional LMs. Thus, a large process memory is usually required when a DLM is used. One method for overcoming this problem is the pruning approach, which makes a model compact by removing redundant parameters (features). This is basically easy to use even for application developers without special knowledge of the target task, and it is very effective in expanding the availability of LMs to a variety of devices. Pruning methods have already been proposed for back-off n-gram LMs but not for DLMs [9]. A pruning method for DLMs [10] is described in section 3.2 and experimentally evaluated in section 4.

2. Discriminative language models (DLMs)

This section reviews the fundamental features of DLMs and how they are used in ASR, assuming this to be one of the most typical usages. DLMs are generally designed on the linear model, i.e., a^Tf (s), where a is a parameter vector, f is a feature vector of a sentence s, and ^T is a transpose. Usually, n-gram Booleans are used as features. Where f_k(s) represents the k-th element of the feature vector f (s), they are defined as f_k(s) = 1 when s contains the k-th n-gram and 0 otherwise. For example, if a bigram ‘yeah I’ corresponds to the k-th element, f_k(s) is 1 when s contains ‘yeah I’ and 0 otherwise.

The problem of finding the best sentence from a sentence set using a DLM can be formulated as

where L = {s_j|j = 1, 2, …, N} denotes a set of sentences, f₀(s) denotes the initial score of sentence s, and a₀ is a scaling constant, which can be decided using a development set. In ASR, L is a recognized sentence set, i.e., a hypothesis set, which is generated from each utterance using a baseline speech recognition system, and f₀ is the recognition score. In short, DLMs perform as rerankers, whose purpose is to locate the reference sentence at the top of the list of hypotheses [5], [11], [12].

The value of parameter vector a is decided using a training set, which comprises lists of hypotheses and their references. All the hypotheses in the lists and the reference sentences are converted into feature vectors before training; they are denoted by f_i,j and f_i,r, where i and j represent the indexes of utterance and hypothesis, respectively. In addition, some learning machines use weight e_i,j, which indicates the incorrectness of a sentence. Typically, the word error rate (WER), which is the ratio of the number of misrecognized words to the number of reference words, is used for DLM training [8], [13].

The purpose of training a DLM is to find value a that minimizes an objective function. Each learning machine is characterized by a specific objective function. Given an objective function, the minimization problem can be solved using general parameter estimation methods such as the gradient descent method and the quasi-Newton method. The objective functions of conventional learning machines, i.e., the weighted global conditional log-linear model (WGCLM) [5], [7] and minimum error rate training (MERT) [13], are given by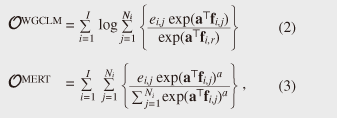

respectively.

3. New techniques

3.1 Discrimination in round-robin fashion

3.1.1 Background

Objective functions are typically formed of an accumulation of loss functions. The definition of loss greatly affects the behavior of the model. The loss functions of WGCLM and MERT correspond to the terms in brackets { } in the equations of their objective functions.

The WGCLM loss function is designed only to distinguish a reference from a hypothesis. In other words, where two hypotheses are given, WGCLM does not distinguish which is the better hypothesis. Hence, a model trained using WGCLM will not perform properly when a list consists of erroneous sentences. By contrast, MERT trains a model so as to distinguish hypotheses having a relatively low error rate from the other hypotheses, without directly distinguishing references from the hypotheses. Therefore, a MERT-trained model will not be able to find the reference when the list contains many low-error-rate sentences together with the reference.

As a result, when a list contains a non-erroneous sentence that is identical to the reference, WGCLM performs more properly than MERT; otherwise, MERT is better than WGCLM. One way to avoid the problem of the best learning machine depending on datasets is to design a loss function that incorporates the characteristics of both WGCLM and MERT.

3.1.2 New technique: round-robin duel discrimination (R2D2)

This section introduces a novel learning machine that possesses the abovementioned characteristics of both WGCLM and MERT. It consists of the loss function

In this loss, a reference (zero error rate hypothesis) is distinguished from another hypothesis, and a hypothesis is distinguished from a higher-error-rate hypothesis. Since an objective function is an accumulation of loss functions, the objective function of the new learning machine is given by

In this objective function, the hypotheses in a list are distinguished from each other in round-robin fashion. Hence, this new learning machine is called round-robin duel discrimination (R2D2) [8].

R2D2 requires a heuristic for avoiding a zero denominator. For this purpose, exp(σe_i,j) is used instead of e_i,j, where σ is a hyperparameter. In this case, the loss function of R2D2 is the same as the WGCLM loss function when σ in the denominator is −∞. In other words, R2D2 is an expansion of WGCLM; hence, R2D2 can perform at least as well as, and potentially better than, WGCLM.

R2D2 also has other advantageous characteristics. One is the concavity of the objective function, which means that convergence to the global optimal solution is promised. In addition, there is an efficient method for calculating the term of double summations over j and j’. This term can be calculated in O(N), although the direct calculation takes O(N²). As a result, R2D2 can train a model in almost the same computation time as WGCLM and MERT.

3.2 Pruning method for DLMs

This section describes a pruning method developed for DLMs [10]. This method can be applied to linear models. It assumes that model parameter vector a is pruned to â_m = R_m^Ta, where R_m = [r₁, r₂, …, r_m] is a matrix consisting of m-tuple n-dimensional orthogonal bases, i.e., rk^Trk’ = δk.k’(δk.k’ is a Kronecker’s delta). Therefore, the score of the pruned linear model is given by For simplicity, only one of the elements of r_k is 1 and all the other elements are zero. Hence, R_m can be regarded as a matrix that removes n − m elements of a and permutes the remaining elements.

The permutation of the parameter elements is decided on the basis of square error metric

where S is a dataset and F is a diagonal matrix whose diagonal elements are f. E_m is an approximation of and can be obtained by assuming that f is sparse, i.e., f_kf_k’ = 0 for k k’. Considering that can be written in a recurrence formula as

where K denotes the index of the element whose value is 1 in r_m+1. The second term represents the impact of removing the K-th dimen­sion in the total error. Namely, the elements of a must be permuted to satisfy η_K1 ≥η_K2 ... ≥ η_Kn.

In summary, this pruning method simply calculates η_k for all the elements and sorts in order of η_k. Then, the top m elements of the sorted parameter are retained and the others are discarded.

4. Experiments

In this section, the two techniques introduced in this article are evaluated through ASR experiments. First, using a baseline ASR system, which is a state-of-the-art system, 5000 hypotheses were generated from each utterance in three different corpora—CSJ-A, CSJ-O, and MITLC—for both training and evaluation. Then, for each corpus, three DLMs were trained, i.e., one each by using WGCLM, MERT, and R2D2. The DLMs were evaluated by WER for the hypothesis with the highest score among the 5000 hypotheses, which were reranked by each of them. Features used here were uni-, bi-, and trigrams of words and parts of speech. Table 1 shows the WERs for the three DLMs (WGCLM, MERT, and R2D2) and for no DLM (w/o DLM). R2D2 provided the best performance with all of the corpora, while WGCLM outperformed MERT with CSJ-A and CSJ-O, but not with MITLC.

Table 1. WERs before and after reranking the 5000-best hypotheses using DLMs.

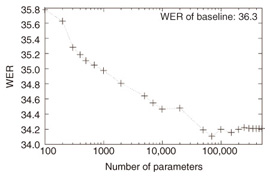
Next, the pruning method was evaluated. The training set in CSJ-A was used for both training a DLM and obtaining statistics for pruning, and the pruned models were then evaluated with the CSJ-O evaluation set. This simulated a cross condition. The learning machine used here was R2D2. The initial model, which was the model before pruning, consisted of more than 10 mega-parameters. The WER of the baseline system, i.e., the WER before reranking, was 36.3. The relationship between WER and model size, i.e., the number of parameters, is shown in Fig. 1. Results for pruned models with over 500,000 parameters are omitted from the figure because the WER differences were very small. This means that the original DLM contains many redundant parameters, and they can be removed effectively by using the pruning method. Even when a 10,000-parameter model was used, the WER degradation was only 0.3.

Fig. 1. Effectiveness of pruning. Pruned model size and WER.

5. Conclusion

After reviewing the fundamental features of DLMs and an example of their use in ASR, this article introduced a novel learning machine and a pruning method for DLMs. The novel learning machine is very effective for generating an accurate model and performs well under various conditions; the pruning method enables us to use a DLM on a variety of devices. They can expand the availability of DLMs, so they will contribute to the development of many kinds of intelligence applications.

References

Takanobu Oba Researcher, NTT Communication Science Laboratories. He received the B.E., M.E., and D.Eng. degrees from Tohoku University, Miyagi, in 2002, 2004, and 2011, respectively. Since 2004, he has been engaged in research on spoken language processing at NTT Communication Science Laboratories. He received the 25th Awaya Kiyoshi Science Promotion Award from the Acoustical Society of Japan (ASJ) in 2008. He is an affiliate member of IEEE and a member of the Institute of Electronics, Information and Communication Engineers, and ASJ.