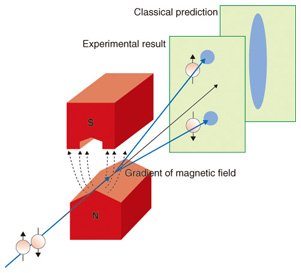
Electron Spin Rotation and Quantitative Determination of Spin-Orbit Coefficients

1.1 Spin in conventional electronic devices

An electron has not only a charge degree of freedom but also a spin degree of freedom associated with the spin angular momentum. If a charged particle has angular momentum, magnetic moment is generated. Therefore, each electron, having a spin angular momentum, acts as a micromagnet. The spin degree of freedom can be interpreted, in one way, as the freedom in the orientation of the micromagnet. In other words, spin is not a conserved quantity. Thus, it has not been easy to use them in conventional devices. Recently, research on electron spin in semiconductors has become increasingly important because future technologies that will transcend existing concepts, such as quantum computers based on spin qubits, will be based on current basic research such as the fundamental research studies described in this article.

1.2 Spin and magnetic moment

While spin is naively interpreted as a micromagnet, its quantum mechanical properties are complicated and the spin sometimes behaves contrary to everyday experience. For example, one would associate the word spin with the spin of a tennis ball, where the magnitude of the ball’s angular momentum can be varied continuously by applying a torque. However, the spin of an electron cannot be varied continuously. To describe such peculiar properties of electron spin, we dare to provide a quantum mechanical explanation of electron spin in this article.

1.3 The Stern-Gerlach experiment

The fact that the magnitude of electron spin is not continuously variable but takes only discrete values was confirmed by the Stern-Gerlach experiment (Fig. 1) [1]. While tiny particles of silver were used in the actual experiment, the experimental results reflect the properties of electron spin. When electrons pass through space containing a magnetic field whose magnitude is graded in the perpendicular direction, their spins are decoupled into two states with different magnetic moments, as if they have been sorted (taking a bar magnet as an example, these are an up-spin state with the south (S) magnetic pole facing upward and a down-spin state with the S pole facing downward). A straightforward interpretation of the measured results leads to the conclusion that the magnetic moment of electron spins can take only two values: either the value corresponding to the upward direction or the value corresponding to the downward direction. Then, might there be electrons with a spin state that is neither upward nor downward vertically, such as those whose S pole is pointing horizontally among the electrons that have passed through the detector? To give the conclusion first: yes, there are such electrons. To understand why and to make correct predictions about spin-related phenomena in semiconductor devices, we need an accurate understanding of quantum mechanics.

Fig. 1. Stern-Gerlach experiment.

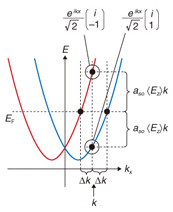
1.4 Probability interpretation of the wave function and reduction of the wave packet

Two well-known concepts in quantum mechanics are probability interpretation (of the wave function) and reduction of the wave packet. Considering a one-dimensional world for simplicity, let us express the wave function of an electron by Ψ(x).

Probability interpretation means the following. When we try to measure the location of an electron described by Ψ(x), the probability that the electron is found at a position between x and x+Δx is given by |Ψ(x)|²Δx. Reduction of the wave packet is related to probability interpretation. It is a term that describes how an electron in a state with a wide probabilistic distribution |Ψ(x)|² (wave packet) before measurement collapses to a point at a certain position x as a consequence of the measurement.

1.5 Spin states other than up and down

Besides an electron’s position, its spin state is also more correctly described by a wave function. If we apply the concept of reduction of the wave packet, then the Stern-Gerlach experiment is interpreted as the collapse of the wave function of electron spin to either an up state or a down state by measurement. We note that the up/down direction is the direction of the magnetic field (z direction) within the experimental apparatus (detector).

Since we have freedom in the direction of the magnetic field to be set in the detector of the experimental apparatus, we can also select any arbitrary direction for the observation of a magnetic moment. We would like to emphasize that the phenomena we are explaining here are not related to the torque that the magnetic field in the detector may apply to the electron spin to change its orientation. We are saying that the orientation of the spin is varied as a result of the reduction of the wave packet.

To understand the above description, one needs to know that any state (wave function) of electron spin is described by a wave function a|↑⟩_z + b|↓⟩_z=, which is a superposition of the up-spin ≡ |↑⟩_z and down-spin ≡ |↓⟩_z wave functions. One needs to accept the quantum mechanical conclusion that the probabilities of observing the up- and down-spin states upon measurement of spin state a|↑⟩_z + b|↓⟩_z= are given by |a|² and |b|², respectively, where a and b are complex numbers such that |a|² + |b|² = 1. Moreover, if we perform the measurements on the same spin state a|↑⟩_z + b|↓⟩_z= while varying the direction of the magnetic field in the detector, we will find a certain direction for which observation of only up-spin electrons will result (up-spin with respect to the chosen magnetic field direction). This direction is called the direction (or orientation) of the electron spin. Generally, electron spin orientations differ from one electron to another. However, the conclusion of quantum mechanics is that any electron spin can be expressed as a|↑⟩_z + b|↓⟩_z by finding appropriate complex numbers a and b, whichever direction it is pointing in.

From the above discussion, we can conclude the following. If there are two spin states |↑⟩_x and |↓⟩_x that are orientated in the +x and -x directions, respectively, we should be able to write them as a superposition of |↑⟩_z and |↓⟩_z, which ultimately leads to |↑⟩_x=(|↑⟩_z + |↓⟩_z) and |↓⟩_x=(|↑⟩_z – |↓⟩_z). If we interpret this probabilistically, then the probability that a spin-up or spin-down state is detected (with respect to the z direction) is 50% upon the measurement of these spins. Conversely, the state a|↑⟩_z + b|↓⟩_z can also be written as |↑⟩_x + |↓⟩_x using |↑⟩_x and |↓⟩_x. Therefore, if the direction of the magnetic field in the detector is in the x direction, the up- and down- spin states will be observed with probabilities and , respectively.

We finally ask which direction is the electron spin a|↑⟩_z + b|↓⟩_z pointing in? We provide only the conclusion here. The three-dimensional vector for the orientation of this spin is (x, y, z) = (2Re(a*b), 2Im(a*b), |a|² – |b|²) , where Re(a*b) and Im(a*b) are the real and imaginary parts of the complex number a*b, respectively.

1.6 Spin splitting due to the Rashba effect

In our research, we use a spin-orbit interaction called the Rashba effect [2] in controlling electron spins. A Hamiltonian^*1 of the spin-orbit interaction generally takes the form (∇V×p)•σ. Using the confinement potential V(z) of the quantum well for V, i.e., ∇V(z) = (0, 0, -eE_z), and ħk for p (momentum), we obtain the Hamiltonian for the Rashba effect as H_R = a_so 〈E_z〉 (k_yσ_x – k_xσ_y). Here, a_so is a material-dependent intrinsic constant for the Rashba effect, 〈E_z〉 is the expectation value of E_z, and σ_x and σ_y are the Pauli spin matrices.^*2 If we use a plane wave for the orbital part of the wave function for simplicity with a two-dimensional wave vector k≡(k_x, k_y)=(k, 0), the wave functions (eigenfunctions) including the spin part are given by with respective eigenenergies ± a_so 〈E_z〉k. Thus, the energy splitting between the two states at a constant wave vector, which is caused by a spin-orbit interaction associated with the confinement potential of semiconductor heterostructures, is called the Rashba splitting^*3 (Fig. 2).

Fig. 2. Energy dispersion of two-dimensional electron system with the Rashba splitting.

1.7 Spin rotation

Consider a superpositioned wave function that is composed of two wave functions associated with two points on the Fermi surface^*4 (k±Δk, 0), where Δk = a_so 〈E_z〉 m*/ħ², in a system having the Rashba splitting. The spin part of this wave function at x = 0 is , where the spin is orientated in the z direction. The electron spin states for x ≠ 0 are = , the spin orientation of which is (sin(2Δkx), 0, cos(2Δkx)) in a three-dimensional vector. Thus, the spin rotates in the x-z plane as a function of the electron’s position x. An electron in a semiconductor can be regarded as a wave packet having a central wave number. Since the propagation speed of a wave packet is given by its group velocity (Fermi velocity), an electron in uniform linear motion changes its position according to its Fermi velocity. Thus, the spin orientation will rotate accordingly. The angular velocity of the electron spin rotation is given as ω = 2a_so 〈E_z〉 k/ħ in this case. The tunability of 〈E_z〉 by an external gate or a specific design of the heterostructure enables us to control the angular velocity of spin rotation, which is one of the greatest attractions of the Rashba effect. Some examples of spin rotation for an electron moving at the Fermi velocity are shown in Fig. 3, where a_so acts as a parameter indicating how easy it is to control the electron spin precession by an electric field 〈E_z〉.

Fig. 3. Examples of spin precession.

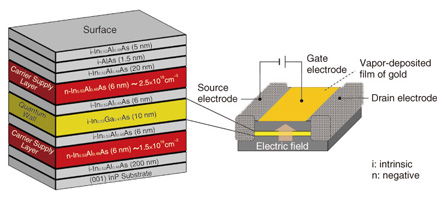
In research on the Rashba effect up to now, it has been important to obtain a value called the Rashba coefficient α, which corresponds to a_so 〈E_z〉. Pieces of circumstantial evidence showing that the α values are controllable by a gate had been accumulated, though nobody had been able to show a quantitatively linear relationship between α and 〈E_z〉. The factors that have delayed the progress of this research include (1) a lack of experimental methods that enable one to measure the value of 〈E_z〉 within a quantum well directly and (2) uncertainty about the size of the Dresselhaus spin splitting (the spin splitting arising from the bulk inversion asymmetry), which coexists with the Rashba spin splitting. In collaborative work between Hokkaido University and NTT Basic Research Laboratories, we have demonstrated the linear relationship α = a_so 〈E_z〉 quantitatively by using In_0.53Ga_0.47As semiconductor quantum wells (Fig. 4), which are lattice-matched to (001) InP; this led to the successful quantitative determination of the value of a_so [3]. A key to our success was the coincidental discovery of an epitaxial wafer that has the property that the value of 〈E_z〉 can seemingly be varied from positive to negative values by means of gating. Careful experiments with this epitaxial wafer and a series of similar wafers resulted in our quantitative determination of a_so.

Fig. 4. Experimental sample and FET structure.

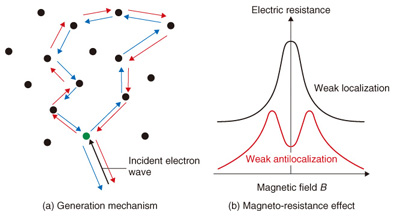
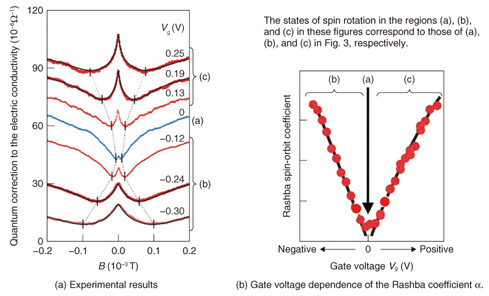
2.1 Experimental procedure for determining a_so

The testpiece used in our experiment was a 10-nm-thick In_0.53Ga_0.47As semiconductor quantum well grown on the (001) plane of an InP substrate (with barrier layers of In_0.52A1_0.48As). We controlled the electron density and the perpendicular electric field 〈E_z〉 within the quantum well by means of a surface gate in a field-effect-transistor structure (Fig. 4). We used a dilution refrigerator to cool the sample down to ~100 mK (electron temperature), in order to minimize the effect of thermal disturbance and increase the measurement sensitivity, and measured the electric resistance as a function of the perpendicular magnetic field (magneto-resistance) for various gate voltages. In these measurements, a distinctive phenomenon called the weak antilocalization appeared in the vicinity of zero magnetic field, owing to the interference of the electron wave functions. We were able to determine the value of the Rashba coefficient α by theoretically analyzing this experimentally observed phenomenon [4].

2.2 Weak localization and weak antilocalization effects

Weak localization is a phenomenon that occurs when an electron is scattered sequentially in a loop by impurities distributed randomly in the conductor, whereby the electrons are weakly localized in the loop as a result of constructive interference of the wave functions. For example, if an electron happens to follow the closed path indicated by blue arrows in Fig. 5(a) after the injection of the electron as indicated by the black arrow, then the red path, which is the time-reversed path of the blue one, should also be present quantum mechanically with the same probability as the blue path. Since the lengths of the two paths are exactly equal, constructive interference always occurs at the endpoint of the two paths (the position of the green impurity in Fig. 5(a)), if the electron propagation is not accompanied by spin rotation. This results in enhancement of the backscattering probability. This is the mechanism of weak localization.

Fig. 5. Weak localization and weak antilocalization effects.

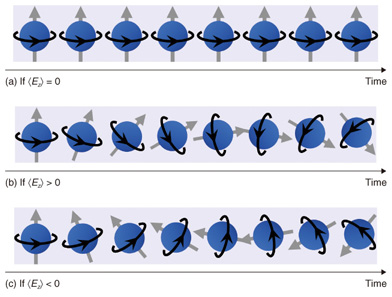
The weak localization effect is partially destroyed if a magnetic field is applied perpendicular to the quantum well. As a result, a negative magneto-resistance appears in the vicinity of the zero magnetic field, as shown by the black curve in Fig. 5(b). The weak localization effect observed in the vicinity of zero magnetic field is also suppressed by the rotation of spins, which is called weak antilocalization. In a more precise description, the mechanism of the weak antilocalization is related to the non-commutativity of spin rotation operators (AB ≠ BA for arbitrarily chosen A and B). This results in a positive magneto-resistance if the weak antilocalization is occurring (the red curve in Fig. 5(b)).

The results of our experiment are shown in Fig. 6(a), where the electric conductivity of a quantum well sample is plotted (on the vertical axis) as a function of the magnetic field (horizontal axis) for various values of the gate voltage Vg. It is necessary to invert the + and - signs on the vertical axis (or invert up and down) when comparing the results with the schematic weak localization/antilocalization effects shown in Fig. 5(b) because the data plotted here are the electric conductances, not the resistances. Because V_g is a relative quantity, its value is set to 0 V when the Rashba splitting is minimized in this analysis. This experimental result shows that the weak antilocalization effect becomes stronger as the absolute value of Vg increases. Then, the value of the Rashba coefficient α can be extracted from the values of the fitting parameters that fit the experimental result best assuming a recently developed theoretical model. The gate voltage dependence of the Rashba spin-orbit interaction coefficient α of this sample obtained from such analyses is shown in Fig. 6(b). We note that the angular velocity of the electron spin rotation rises faster as α increases. The fact that we successfully made accurate predictions of the values of α as a function of the gate voltage V_g as in Fig. 6(b) indirectly means that we succeeded in controlling the angular velocity of the electron spin rotation freely by means of the gate of a transistor. For example, we can rotate the spins of electrons within a semiconductor about some specific axis ((b) in Fig. 3), halt the rotation ((a) in Fig. 3), and rotate them in reverse ((c) in Fig. 3) all by means of a gate. As a result, we expect that the knowledge acquired in this research will bring us one step closer to being able to utilize electron spins in future electronic devices such as quantum computers and ultra-low-power logic devices.

Fig. 6. Measurement of weak localization and weak antilocalization.