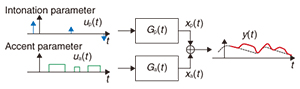
Generative Modeling of Voice Fundamental Frequency Contours for Prosody Analysis, Synthesis, and Conversion

Abstract

This article introduces a state-of-the-art technique that makes it possible to convert speech to different speaking styles through the manipulation of the fundamental frequency (F₀) contour without destroying the naturalness of the speech. This technique can be used, for instance, to convert non-native speech to native-like speech, and to convert normal speech to speech with a more lively intonation similar to the way broadcasters speak. It can also be incorporated into text-to-speech systems to improve the naturalness of computer-generated speech.

Keywords: prosody, intonation, accent, voice fundamental frequency contour, generative model

1. Introduction

The fundamental frequency (F₀) contour refers to the time course of the frequency of the vocal fold vibration of speech. We usually use not only words and sentences to convey messages to the listener in daily communication, but also F₀ contours to add extra flavor to speech such as the identity, intention, attitude, and mood of the speaker. It is also important to note that the naturalness of F₀ contours is one of the most significant factors that affect the perceived naturalness of speech as a whole. In fact, synthesized (artificially created) speech with an unnatural F₀ contour often sounds robotic, lifeless, or emotionless. This article introduces a technique that makes it possible to convert the speaking style of an input utterance into different speaking styles by controlling the F₀ contour while retaining its naturalness.

The proposed technique can be used, for example, to convert the intonation of the speech uttered by a non-native speaker to a more fluent intonation similar to the way native speakers speak, to convert the accents of speech to those with different dialects, and to convert the intonation of normal speech to a more lively intonation similar to the way broadcasters speak. It would also allow us to modify the intonation or accents of the acted speech by actors or actresses as desired without the need to retake the scene. It can also be incorporated into text-to-speech (TTS) systems to improve the naturalness of computer-generated speech. Furthermore, we can build a self-training system to assist students in improving their presentation and language skills. We are also interested in applying the proposed technique to develop a speaking-aid system that makes it possible to convert electrolaryngeal speech to normal speech, which can be used to assist people with vocal disabilities.

2. Fundamental frequency contour (intonation and accent)

The F₀ contour of speech consists of intonation and accent components. The intonation component corresponds to the relatively slow F₀ variation over the duration of a prosodic unit, and the accent component corresponds to the relatively fast F₀ variation in an accented syllable. Both of these components are characterized by a fast rise followed by a slower fall. The former usually contributes to phrasing, while the latter contributes to accentuation during an utterance. In Japanese, for example, changing the positions of accents results in speech with different dialects or meanings. The magnitudes of these components correspond to how much emphasis the speaker intends to place on the associated phrase or accent. Thus, the magnitudes and positions of these components assist the listener in interpreting an utterance and draw attention to specific words. The F₀ contour also plays an important role in conveying to the listener various types of non-linguistic information such as the identity, intention, attitude, and mood of the speaker.

3. Generative modeling of F₀ contours

3.1 F₀ control mechanism

F₀ contours are controlled by the thyroid cartilage, which sits in front of the larynx. The assumption that the F₀ contour of speech consists of intonation and accent components is justified by the fact that the thyroid cartilage involves two mutually independent types of movement with different muscular reaction times. Specifically, the intonation and accent components respectively correspond to contributions associated with the translation and rotation movements of the thyroid cartilage. In the late 1960s, Fujisaki proposed a well-founded mathematical model that describes an F₀ contour as the sum of these two contributions [1, 2] (Fig. 1). This model approximates actual F₀ contours of speech fairly well when the model parameters are appropriately chosen, and its validity has been demonstrated for many typologically diverse languages. If we can estimate the movements of the thyroid cartilage automatically from a raw F₀ contour, we can simulate or predict the F₀ contour that we may observe when the thyroid cartilage moves differently, by simply modifying the values of the motion parameters. Since the movements of the thyroid cartilage are characterized by the levels and timings of the intonation and accent components, one important challenge is to solve the inverse problem of estimating these components directly from speech. However, this problem has proved difficult to solve. This is because it is difficult to determine a unique intonation and accent component pair only from their mixture (namely an F₀ contour), in the same way that it is impossible to determine a unique X and Y pair only from X + Y = 10. Several techniques have already been developed but so far with limited success.

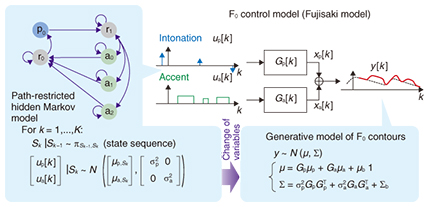
Fig. 1. F₀ control model (Fujisaki model).

3.2 Statistical formulation

There are some clues that can possibly help solve this problem. That is, we can use the fact that the levels and timings of intonation and accent components are statistically biased in normal speech. The author has proposed constructing a stochastic counterpart of the Fujisaki model that makes it possible to use statistical inference techniques to accurately and efficiently estimate the underlying parameters of the Fujisaki model [3, 4]. The problem of estimating the intonation and accent components from a raw F₀ contour is somewhat similar to the audio source separation problem. Audio source separation refers to the problem of separating the underlying source signals from mixed signals. Even though it looks as difficult as solving the X + Y = 10 problem, a statistical approach utilizing the statistical properties and the statistical distribution of the waveforms of audio signals has proved effective in solving it. The idea for the proposed method was inspired by this idea (Fig. 2).

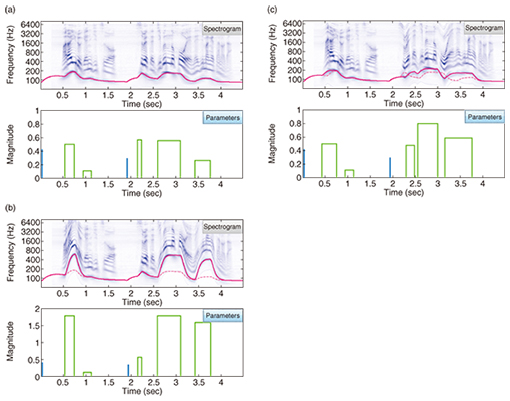
Fig. 2. Proposed model (a stochastic counterpart of the Fujisaki model, described by a discrete-time stochastic process).

An example of the estimated parameters related to the intonation and accent components (blue and green lines) along with the estimated F₀ contours (red line) plotted on the spectrogram of the input speech is shown in Fig. 3(a). An example of converted speech with magnified accent components is shown in Fig. 3(b), and an example of converted speech with shifted positions of accent components is in Fig. 3(c). It is important to note that in these examples we were able to convert the speaking style of the input speech into different styles (one with prominent accents and the other with a different dialect) while retaining the naturalness as if the same speaker were uttering the same sentence in a different way. This was made possible because the proposed framework allows us to modify F₀ contours in such a way as never to violate the physical constraint of the actual F₀ control mechanism.

Fig. 3. (a) Example of the estimated parameters related to intonation and accent components (blue and green lines) along with the estimated F₀ contours (red line) plotted on the spectrogram of the input speech; (b) example of converted speech with magnified accent components; (c) example of converted speech with shifted positions of accent components.

4. Future perspective

While linear predictive coding (LPC), proposed in the late 1960s, led to the development of a speech analysis/synthesis system that provides a powerful parameter estimation framework for the vocal tract model, the proposed technique enables a new system that does the same for the F₀ control model (i.e., the Fujisaki model). In a way similar to the development of LPC, which has given rise to modern speech analysis/synthesis and become the cornerstone module for today’s mobile and voice-over-IP (Internet protocol) communication, this work can also potentially open the door to a brand new speech analysis/synthesis framework.

Acknowledgment

This work was carried out in collaboration with the members of Sagayama/Moriya/Kameoka laboratory of the University of Tokyo. I thank all the people who contributed to this work. This work was supported by JSPS KAKENHI Grant Number 26730100, 26280060.

References

[1]	H. Fujisaki and S. Nagashima, “A Model for the Synthesis of Pitch Contours of Connected Speech,” Annual Report of the Engineering Research Institute, The University of Tokyo, Vol. 28, pp. 53–60, 1969.
[2]	H. Fujisaki, “A Note on the Physiological and Physical Basis for the Phrase and Accent Components in the Voice Fundamental Frequency Contour,” Vocal Physiology: Voice Production, Mechanisms and Functions, pp. 347–355, Raven Press, New York, USA, 1988.
[3]	H. Kameoka, J. Le Roux, and Y. Ohishi, “A Statistical Model of Speech F₀ Contours,” Proc. of SAPA 2010 (the 2010 Workshop on Statistical and Perceptual Audition), pp. 43–48, Makuhari, Japan, Sept. 2010.
[4]	H. Kameoka, K. Yoshizato, T. Ishihara, K. Kadowaki, Y. Ohishi, and K. Kashino, “Generative Modeling of Voice Fundamental Frequency Contours,” IEEE/ACM Trans. Audio, Speech and Language Processing, Vol. 23, No. 6, pp. 1042–1053, 2015.

Hirokazu Kameoka: Distinguished Researcher, NTT Communication Science Laboratories.
He received his B.E., M.S., and Ph.D. from the University of Tokyo in 2002, 2004, and 2007. His research interests include audio, speech, and music signal processing and machine learning. He received 13 awards over the past 10 years, including the IEEE (Institute of Electrical and Electronics Engineers) Signal Processing Society 2008 SPS Young Author Best Paper Award. He is the author or co-author of about 90 articles in journal papers and peer-reviewed conference proceedings. He is currently also an Adjunct Associate Professor at the University of Tokyo.

↑ TOP