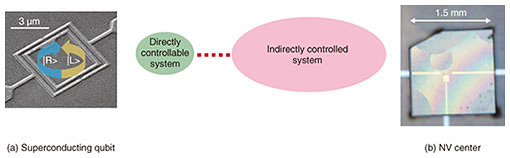
Quantum Information Processing via Indirect Quantum Control

1. Current status of quantum information processing

A quantum computer is a quantum-information-processing device that uses the properties of quantum mechanics, which allows two states to exist at the same time. As a result, a quantum computer can naturally perform parallel processing to do things that are impossible with today’s computers. For example, it can easily decode any encrypted code currently in use, which is one of the reasons the implementation of quantum computers is greatly anticipated. Another type of quantum information processing is quantum cryptography. This type of cryptography uses a property of quantum mechanics that makes it impossible to measure certain quantities at the same time and is secure in principle. Quantum cryptography is expected to complement the modern cryptography techniques currently in use.

In terms of practical application, devices that implement quantum cryptography have been developed. Although these devices are not currently available to the public, they can be used in special cases. It is only a matter of time before they are introduced into the real world. In fact, the governments of China, the EU, and the United States are conducting field experiments using quantum cryptography.

However, we are still a bit far from the application of quantum computers. An article authored by Google researchers showed how an implemented quantum computer outperforms conventional computers, and IBM offers a service to use a quantum computer on the cloud. Quantum computers made up of a few tens of qubits have been constructed. However, we are not yet ready to implement a quantum computer of a scale and level of accuracy that could change the nature of society. For example, to crack the ciphers currently in use on the Internet, we need thousands of ideal qubits. If just a little noise is left on the qubits, we would need millions of them to crack the ciphers. In other words, the scale of current quantum computers is still an order of magnitude too small to have any kind of significant impact on society.

There are currently two problems that need to be overcome to increase the scale of quantum computers. The first problem is the increase in noise. No matter how small a quantum system, which is composed of quantum computers and other quantum devices, is, it is impossible to completely eliminate noise in quantum computers. Moreover, as the scale of quantum computers increases, the effect of noise becomes greater. This is why we need to find ways to avoid the increase in noise as we increase the scale of such computers. Quantum error-correcting codes are the most promising to overcome this problem. However, they are in the research phase and not yet ready for practical use. The other problem is that the mechanisms needed to control large-scale quantum computers are difficult to implement. In a typical quantum computer model, the number of control mechanisms is proportional to the number of qubits that make up the quantum computer. In other words, as the number of qubits in a quantum computer increases, a vast number of control mechanisms—in the millions—is required. This makes device design very difficult. Conventional computers have overcome the same problem with the concept of a bus, but a quantum structure for what one might call a quantum bus has not yet been developed for large-scale quantum computers.

2. Indirect quantum control as a means of overcoming the problems in developing quantum computers

Although various studies have used well-known techniques in attempts to overcome the above problems, it is also important to explore solutions from a new perspective. The idea of indirect quantum control will be just such a new solution.

An indirect quantum protocol is a means of controlling a quantum system via direct manipulation of a part (system S) of the system. That is, the rest of the parts (system E) are controlled indirectly via the interaction between them and system S.

An example of system S is a qubit system that is easy to manipulate. It is composed of superconducting qubits (one such qubit is shown in Fig. 1(a)) and has superconducting material arranged in a ring shape. A nitrogen-vacancy (NV) center is an example of system E composed of one qubit. It is made from a lattice defect caused by nitrogen in diamonds (Fig. 1(b)). Simply placing a diamond plate containing NV centers on top of a superconducting qubit connects the two quantum systems through their interaction. Thus, a structure for indirect quantum control can be created. Experiments to implement a one-qubit quantum memory system with little noise [1] have been carried out using this structure.

Fig. 1. Indirect quantum control.

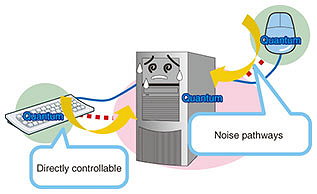
This indirect quantum control structure is generally effective in overcoming the first problem mentioned above, namely the increase in noise. It can be understood as follows. To manipulate a quantum system, it is necessary to place physically implemented manipulators in it. However, if such manipulators are connected, they also allow noise pathways to enter the system (Fig. 2). If we want to reduce noise ingress, we have to sacrifice operability by reducing such manipulators. In other words, there is a trade-off between ease of operation and noise reduction in the quantum system. The current implementation of quantum computers relies on the high operability of the entire quantum system. This imposes a limitation on reducing the noise-intrusion paths. Therefore, if it is possible to have complete controllability via limited operability, we will be able to reduce the noise ingress paths and achieve a high level of noise reduction.

Fig. 2. Noise ingress.

The ability to control the entire quantum system by indirect quantum control is a solution to the second problem mentioned above. When a quantum system is completely and indirectly controlled, any quantum information in system E must merge into system S at some point. Such information is manipulated on system S at that particular time and returned to system E. This is abstractly the function of the quantum bus. In other words, the capability of perfect control via large-scale indirect quantum control includes the function of a large-scale quantum bus.

3. Challenges in implementing quantum computers with indirect quantum control

As mentioned above, we can overcome the two main problems to constructing large-scale quantum computers by using indirect quantum control. Nevertheless, indirect quantum control has not been considered as a means of large-scale quantum information processing. Though it is used for some small-scale examples of the quantum memory system mentioned above, it has not yet been sufficiently researched. This is because even a small difference in the interaction between systems S and E can significantly affect the type of control that can be implemented. It is not easy even to discuss the ability to process information in such a situation. Any quantum device made up of quantum computers must be completely controlled. However, we have not been able to clearly answer even the basic question of which type of indirect quantum control could meet this requirement.

The research results presented in our recent paper [2] answer this basic question. Given a quantum system, the set of controls performed on it can be identified using a dynamical Lie algebra^*1, which is equal to a linear space made from a set of skew-Hermitian matrices^*2. Therefore, to answer the question of whether a given quantum system has sufficient controllability, it is sufficient to evaluate its dynamical Lie algebra. For example, in the case of typical quantum computers as currently conceived, the corresponding dynamical Lie algebra contains all skew-Hermitian matrices, which means that the quantum system can be completely controlled.

Regarding general quantum systems, however, there are many possible dynamical Lie algebras. This is why it has been difficult to give answers to even the above basic question in indirect quantum control. However, our recent study [2] has shown that, when operation is done by indirect quantum control, the dynamical Lie algebra must possess a Jordan algebra^*3. It is well known that a Jordan algebra is much less diverse than a dynamical Lie algebra. Using this fact, we fully classified the dynamical Lie algebra that can be identified in the case of indirect quantum control and found that indirect quantum control has properties that make it a useful means of implementing quantum information processing.

According to the obtained classification of a dynamical Lie algebra, its structure deeply depends on the dimension^*4 of the quantum system (system S) that can be directly manipulated. When the dimension of system S is three or more, the dynamical Lie algebra always contains arbitrary skew-Hermitian matrices, which act on the space that can be affected by manipulating system S. In other words, if the dimension of system S is three or more, a quantum system behind system S, which may be a part of system E, can be completely controlled. This means that indirect quantum control is a universally sufficient means of implementing quantum information processing.

4. Summary

By studying indirect quantum control mathematically, we can see that it is promising as a means of achieving quantum information processing. Though this will not directly enable us to construct large-scale quantum computers with sufficiently low noise tomorrow, we theoretically proved that indirect quantum control, which has not been used before, is a promising means to overcome serious problems in constructing large-scale quantum computers. This is a significant step forward in itself.

By further developing the theories that explain the properties of dynamical Lie algebras identified in the case of indirect quantum control [2], we will be able to evaluate the execution time of control or plan procedures that implement desired controls. This will further significantly contribute to the construction of quantum computers.

References

[1]	X. Zhu, S. Saito, A. Kemp, K. Kakuyanagi, S. Karimoto, H. Nakano, W. J. Munro, Y. Tokura, M. S. Everitt, K. Nemoto, M. Kasu, N. Mizuochi, and K. Semba, “Coherent Coupling of a Superconducting Flux Qubit to an Electron Spin Ensemble in Diamond,” Nature, Vol. 478, pp. 221–224, 2011.
[2]	G. Kato, M. Owari, and K. Maruyama, “Algebra and Hilbert Space Structures Induced by Quantum Probes,” Ann. Phys., Vol. 412, 168046, 2020.