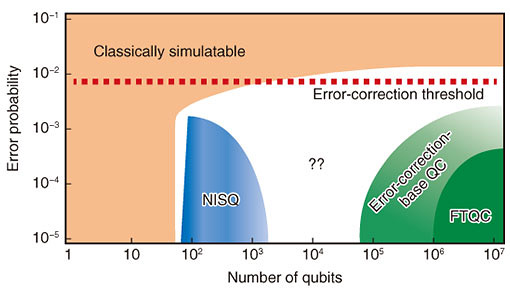
Designing Quantum Computers

1. Introduction

It has been known for almost half a century that the principles of quantum mechanics will allow technologies to be developed that provide new capabilities impossible with conventional technology or significant performance enhancements over our existing ones [1]. These benefits exploit ‘quantum coherence’ and in particular quantum entanglement to some degree for technological advantages in areas ranging from quantum sensing and imaging [2] to quantum communication [3] and computation [4]. While these fields are still in their infancy, we can already imagine a quantum internet connecting quantum computers together that take information from a number of inputs including quantum sensor arrays [5, 6]. Quantum clocks will synchronize all these devices if necessary [7]. How do we move from our few-qubit devices to noisy intermediate-scale quantum (NISQ) processors [8] and ultimately fault-tolerant quantum computers (FTQCs) [9], as depicted in Fig. 1? What is the path to achieve this?

The last decade has seen a paradigm shift in the capabilities of quantum technologies and what they can achieve. We have moved from the ‘in-principle’ few-qubit demonstrations in the laboratory to moderate-scale quantum processors that are available for commercial use. Superconducting circuits, ion traps, and photonics have enabled the development of devices with approximately 50 qubits operating together in a coherence fashion, and important quantum algorithms have already been performed on them. These NISQ processors have shown the capability to create complexity difficult for classical computers to calculate—the so-called quantum advantage [11, 12]. The noisy nature of the qubits, gates, measurements, and control systems used in these NISQ processors however severely limits the size of tasks that can be under taken on them (see Fig. 1). Noise-mitigation techniques may help a little to push the system size up, but fault-tolerant error-correction techniques are required if we want to scale up to large-scale universal quantum computers (machines with 10⁶–10⁸ physical qubits performing trillions of operations). The fundamental question is how we envision this given our current technological status.

Fig. 1. The landscape for quantum computation in terms of resources (number of physical qubits) and error probabilities [10]. The orange-shaded area depicts the regime in which the tasks undertaken on it could also be classically simulated. The bluish area represents the NISQ regime in which tasks can be potentially performed with quantum advantage. Finally, the light-green area represents quantum computers (QCs) using error correction, while the dark-green area is fault-tolerant universal quantum computers.

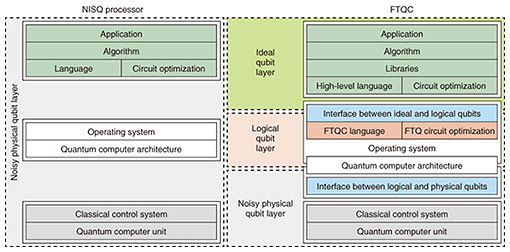
2. NISQ processors and simulators

It is useful to begin our design consideration with an exploration of NISQ processors and simulators. They are fully programmable machines generally designed to undertake a specific range of tasks. In principle, they are universal in nature but noise limits them to being special-purpose machines. They have proved extremely useful in showcasing the potential that quantum physics offers. There are a number of physical systems from which these NISQ processors can be built despite superconducting circuits and ion traps being the most advanced [8]. A processor or simulator is however much more than just a collection of quantum bits (20–100 qubits) working together in some fashion. It is a highly integrated device involving many systems at different levels working seamlessly together, which we illustrate as a one-layer design in Fig. 2. At the top of the layer is the application one wants to perform on the NISQ processors, which could involve, e.g., simulation and sampling. The application can be quite an abstract object, so it is translated into an algorithm giving the instructions/rules that a computer needs to do to complete this task. These instructions are decomposed into a set of basic operations (gates, measurement, etc.) that the processor will run. Such operations are quite generic and not hardware specific. The operating system will take this sequence of gates and determine how they can be implemented on the given processor architecture. The layout and connectivity of the NISQ processor determines what algorithms can be performed. The operating system will turn them into a set of “physical instruction signals/pulses, etc.” that the classical control system (CCS) will perform on the quantum computer unit (QCU). For many of the smaller size processors out there, the high-level aspects of the layer (operating system, architecture and above) are not integrated into the system and instead have been done offline—sometimes by hand. As the number of qubits in the processor grows, the integration of these higher-level aspects becomes critical and quite limiting if it is not done appropriately. Optimizations need to be done both with the algorithm and operating system to minimize the effects of the noisy physical system the program will run on. The coherence times of the qubits, quality of the gates, and measurements will ultimately limit the size of the computation one can perform. One will reach the stage where error always occurs—limiting the usefulness of the NISQ processor for real tasks. With a 100-qubit processor performing 100 gates on each qubit, an error as small 10⁻⁴ still makes it almost certain that the computation will have errors in it.

Fig. 2. Schematic diagram showing the quantum computational “system layers” for both a NISQ processor and future large-scale FTQC. These “layers” show the necessary components from the basic hardware to top-level application. The NISQ processor, the simpler of the two, begins at the lowest level with a QCU involving quantum bits and the necessary mechanism to manipulate them including initialization, controlled dynamics, and measurement and feedback. All such elements are in principle noisy, which directly leads to errors in the computation. The QCU is operated on through a CCS. Above this is the processor architecture and an operating system. At the top of the layer (highest level) we have our “application,” which needs to be written as an algorithm using libraries written in a quantum language with optimization possible. Typically, noisy operations within the QCU limits the size of such processors. The FTQC, on the other hand, has a much more detailed and structured “system layer” arrangement due to the large size of the processor and the requirement to handle errors from the noisy QCU. This involves three layers: the noisy physical qubit layer, the logical qubit layer, and finally the ideal qubit layer. Each layer contains a number of components, and their integration is necessary for the FTQC to operate correctly. An interface is necessary between the various layers. Next the overall system design needs to be considered together as choices in one layer can have a profound effect on another one. Design changes in the upper-level logical qubit layer can force changes in the noisy physical qubit layer and vice versa.

The NISQ processors and simulators are an important step in the development of large-scale universal quantum computers. They have shown us quantum advantage—where the quantum processor even using a modest number of qubits can do something faster than today’s supercomputers using trillions of transistors. This has demonstrated the potential of the quantum approach. More importantly however, these NISQ processors have allowed us to focus on the overall system layer design and how it operates in practice.

3. Error-corrected quantum computers

While error-mitigation techniques can be used to suppress errors to a certain degree (maybe by several orders of magnitude), it seems unlikely that those techniques will scale to much larger processors. One has to establish the means to cope with the noisy nature of the processor. Quantum error correction is an essential tool to handle this but it comes with a large resource cost (due to the necessity of encoding quantum information at the logical level across many physical qubits). As such we immediately notice the blank area in Fig. 1 between the NISQ processor and error-corrected quantum computers. The gap could be many orders of magnitude if one needs to handle quite noisy physical qubits (e.g., 0.1% error probability). One should be operating in the regime in which the use of error correction (and the noisy qubits and gates) does not cause more error than it can fix. Therefore, there may be a number of applications in which a limited amount of error correction helps before full fault tolerance is needed (but with error propagation occurring). This is a largely unexplored but interesting regime. Error-corrected quantum computers should provide a natural bridge to FTQCs, which we consider next.

4. FTQCs

It is important to begin by defining what we mean by an FTQC. It is a more specific form of an error-corrected quantum computer that is able to run any form of computation of arbitrary size without having to change its design. It requires quite a large redesign of the NISQ layer structure. In fact, we need to split it into at least three distinct parts: the noisy physical qubit layer, logical qubit layer, and ideal qubit layer. These layers need to work in unison.

The highest-level layer (shown in green) is similar to that shown in the NISQ approach but is assumed to operate on ideal qubits but with libraries and a high-level language added to it. The purpose of the libraries is to provide useful subroutines the algorithm may need to use. The algorithm is then converted into a sequence of ideal gates and measurement operations (ideal quantum circuits). Circuit-optimization techniques can also be applied to reduce the number of ideal qubits and temporal resources required. It is important to mention that this layer is like a quantum virtual machine and is agnostic to what hardware it is running on. Ideal qubits can have any quantum gate applied to them.

The middle layer is associated with logical qubits and their manipulation. Logical qubits are different from the ideal qubits mentioned above as only a restricted set of gate operations can be applied to them. This is a very important difference. Now, the middle layer acts as an interface to the ideal qubit layer and converts the quantum circuits (code) developed there into operations associated with logical qubits (with the restricted quantum gate sets etc.). These logical qubits are based on fault-tolerant quantum-error-correction codes operating well below threshold. This layer determines which quantum error codes will be used. Associated with these logical qubits are a fault-tolerant model of computation (e.g., braiding and lattice surgery) and a language to describe them [13]. The operation on those logical qubits is then decomposed into a set of physical operations that is passed to the noisy physical qubit layer.

The lowest layer (the noisy physical qubit layer) is similar to that seen in the NISQ processor but its operation throughout the computer is much more regular and uniform in an FTQC. It takes the physical qubit operations passed to it by the middle layer and establishes how they can be performed using the layout and connectivity of the hardware device. The operating system will turn them into a set of physical instruction signals/pulses etc. that the CCS will perform on the QCU.

While these layers have been presented separately, they must work seamlessly together in the FTQC [9]. One cannot assume that small changes within a layer will not significantly affect the other layers. The choice of the quantum-error-correction code within the middle layer for instance puts constraints on the computer architecture and quantum gates being performed within the QCU. Moving to a different code may require a completely different computing architecture.

5. Distributed quantum computers

A key aspect of the noisy physical qubit layer is the quantum computer architecture and the layout/connectivity of qubits and control lines. Like we have seen in the conventional computer world, the size of the monolithic processor becomes a bottleneck to performance. The solution was to go with a multicore approach. We expect a similar bottleneck to occur within our quantum hardware, so we can use a distributed approach with which small quantum processors (cores) are connected together to create larger ones. This modular approach has a number of distinct advantages including its ability to give long-range connectivity between physical qubits [14, 15]. Such modules could accommodate a few qubits through to thousands. This is a design choice, and the optimal size is currently unknown.

6. Discussion

In the design of FTQCs, one must not look only at what occurs within the layers individually. Optimizations in the high-level layer can have a significant effect on the resources required in the middle logical qubit layer, even decreasing the distance of the quantum-error correcting needed [13]. This in turn would mean fewer qubits and gates required at the physical qubit layer. Furthermore, one must be careful not to look at the computing system too abstractly, especially within the lowest layer. One must understand the properties of the physical systems from which our qubits are derived. The choice of physical system and how it is controlled will have a profound effect on the other layers. The fault-tolerant error-correction threshold heavily depends on the structure of the noise the qubits experience in reality.

References

[1]	J. P. Dowling and G. J. Milburn, “Quantum Technology: the Second Quantum Revolution,” Phil. Trans. R. Soc. Lond. A, Vol. 361, No. 1809, 2003.
[2]	V. Giovannetti, S. Lloyd, and L. Maccone, “Quantum-enhanced Measurements: Beating the Standard Quantum Limit,” Science, Vol. 306, No. 5700, pp. 1330–1336, 2004.
[3]	N. Gisin and R. Thew, “Quantum Communication,” Nature Photon., Vol. 1, pp. 165–171, 2007.
[4]	R. P. Feynman, “Simulating Physics with Computers,” Int. J. Theor. Phys., Vol. 21, pp. 467–488, 1982.
[5]	W. J. Munro, K. Azuma, K. Tamaki, and K. Nemoto, “Inside Quantum Repeaters,” IEEE J. Sel. Top. Quantum Electrons., Vol. 21, No. 3, 6400813, 2015.
[6]	K. Azuma, S. Bäuml, T. Coopmans, D. Elkouss, and B. Li, “Tools for Quantum Network Design,” AVS Quant. Sci., Vol. 3, No. 1, 014101, Feb. 2021.
[7]	S. M. Brewer, J.-S. Chen, A. M. Hankin, E. R. Clements, C. W. Chou, D. J. Wineland, D. B. Hume, and D. R. Leibrandt, “27Al+ Quantum-logic Clock with a Systematic Uncertainty below 10−18,” Phys. Rev. Lett., Vol. 123, 033201, 2019.
[8]	J. Preskill, “Quantum Computing in the NISQ Era and Beyond,” Quantum, Vol. 2, 79, 2018.
[9]	K. Nemoto, S. Devitt, and W. J. Munro, “Noise Management to Achieve Superiority in Quantum Information Systems,” Phil. Trans. R. Soc. A, Vol. 375, No. 2099, 20160236, 2017.
[10]	J. Kelly, “A Preview of Bristlecone, Google’s New Quantum Processor,” ai.googleblog.com/2018/03/a-preview-of-bristlecone-googles-new.html
[11]	F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. S. L. Brandao, D. A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, J. R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Yuezhen Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven, and J. M. Martinis, “Quantum Supremacy Using a Programmable Superconducting Processor,” Nature, Vol. 574, pp. 505–510, 2019.
[12]	H. S. Zhong, H. Wang, Y. H. Deng, M. C. Chen, L. C. Peng, Y. H. Luo, J. Qin, D. Wu, X. Ding, Y. Hu, P. Hu, X. Y. Yang, W. J. Zhang, H. Li, Y. Li, X. Jiang, L. Gan, G. Yang, L. You, Z. Wang, L. Li, N. L. Liu, C. Y. Lu, and J. W. Pan, “Quantum Computational Advantage Using Photons,” Science, Vol. 370, No. 6523, pp. 1460–1463, 2020.
[13]	M. Hanks, M. P. Estarellas, W. J. Munro, and K. Nemoto, “Effective Compression of Quantum Braided Circuits Aided by ZX-Calculus,” Phys. Rev. X, Vol. 10, No. 4, 041030, 2020.
[14]	K. Azuma, H. Takeda, M. Koashi, and N. Imoto, “Quantum Repeaters and Computation by a Single Module: Remote nondestructive parity measurement,” Phys. Rev. A, Vol. 85, No. 6, 062309, 2012.
[15]	K. Nemoto, M. Trupke, S. J. Devitt, A. M. Stephens, B. Scharfenberger, K. Buczak, T. Nöbauer, M. S. Everitt, J. Schmiedmayer, and W. J. Munro, “Photonic Architecture for Scalable Quantum Information Processing in Diamond,” Phys. Rev. X, Vol. 4, No. 3, 031022, 2014.