|
|||||||||||||||
|
|
|||||||||||||||
|
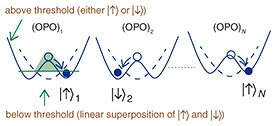
Feature Articles: NTT Research: Open Collaboration to Upgrade Reality Vol. 20, No. 1, pp. 16–19, Jan. 2022. https://doi.org/10.53829/ntr202201fa3 The Future of Problem Solving: The Coherent Ising Machine ApproachAbstractSeveral new computing models tackle combinatorial optimization problems. These include adiabatic quantum computation, also known as quantum annealing, and the coherent Ising machine (CIM). The Physics and Informatics Laboratories at NTT Research launched a CIM initiative, and NTT Basic Research Laboratories built large-scale CIM prototypes. This article reviews the CIM approach, results to date, and future research agenda. Keywords: coherent Ising machine, optimization problems, optical parametric oscillator 1. IntroductionThe current computing model, composed of processing, communication, and memory units, is more than 70 years old. To overcome the inherent limitations of this model, over the past few decades, physicists, computer scientists, and technology companies have been exploring a range of new approaches. A common goal with these alternative models, which use a mix of analog, digital, classical, and quantum technologies, is to solve extremely difficult computational challenges with reduced energy cost. Such challenges commonly target non-deterministic polynomial-time (NP)-hard or NP-complete problems. There are several types of NP-hard problems. One type targets combinatorial optimization, i.e., finding an optimal solution from a large set of candidates. One of the earliest described combinatorial optimization problems was determining the minimum total distance in a journey to N number of cities. Calculated by factorials, the number of combinations becomes astronomically high as N increases. Several new computing models tackle combinatorial optimization problems. These include adiabatic quantum computation, also known as quantum annealing (QA), and a coherent Ising machine (CIM). The Physics and Informatics Laboratories (PHI Lab) of NTT Research launched a CIM initiative, and NTT Basic Research Laboratories built large-scale CIM prototypes. This article reviews the CIM approach, results to date, and future research agenda. 2. Definition of termsTo understand the CIM approach and why it is a type of quantum/classical hybrid computing, let us define some terms, starting with Ising then turning to coherent. The proper name refers to Ernst Ising, a German physicist linked to a mathematical model created in the 1920s to describe magnetic orders. The Ising model originally consisted of a one-dimensional set of discrete variables representing N magnetic moments of atomic spins, each of which has two possible states (+1 or –1). Its energy was expressed in terms of the sum of pair-wise (two-body) interaction, Hamiltonian. Solving the model involves finding its ground state, which is the lowest energy state. If a spin-spin coupling configuration is not simple and cannot be described by planar graphs, finding the ground state of an Ising Hamilton falls into the NP-hard category of computational complexity. The most important active component in a CIM is an optical parametric oscillator (OPO). First demonstrated in 1965, about five years after the invention of the laser, the OPO is a coherent light source. It is distinct from the laser because it produces a quantum state of light (squeezed state). While the Ising model, which evolved from a one- or two-dimensional lattice framework, mathematically represents the atomic spins in any complex configuration, the OPO-based CIM creates a universe of artificial spins, which can then be mapped to a real-world combinatorial optimization problem through an N x N coupling matrix. The solution corresponds to an optimum configuration of spins that minimize their energy function. This system is doubly coherent in the following sense. When one photon is eliminated from a pump pulse sequence at frequency 2ω, two photons (called a photon-pair or biphoton) are generated simultaneously in a signal pulse sequence at frequency ω. If a CIM consists of two OPOs, a single photon pair exists simultaneously in two OPOs as linear superposition. If the CIM consists of N OPOs, a single photon pair exists simultaneously in N OPOs as linear superposition. Therefore, the elementary excitation of the CIM coherently spreads in an entire machine consisting of N OPOs. This fact means that each OPO state simultaneously exists in a vacuum state with a zero-photon state with a large probability and two-photon state with a small probability. Because of this coherent superposition nature, each OPO state occupies 0-phase (down spin) and π-phase (up spin) states even if there is one and only one photon pair in an entire machine. Therefore, a prerequisite for quantum computation, linear superposition of two states, is naturally satisfied in a CIM [1]. 3. Two CIM typesIn practice, there are two types of CIMs: one using an optical delay line (ODL) and the other using measurement feedback (MFB) to introduce the coupling matrices. As mentioned above, the OPO absorbs one photon from the pump field and emits two photons into the signal field simultaneously. As a result of interference among the zero- and two-photon states, the electromagnetic field is stretched into a squeezed vacuum state or a linear superposition of up- and down-spin states. If the pump amplitude is further increased, the stretched noise is finally split apart into the two states with positive and negative average amplitudes. That splitting point marks a transition from quantum to classical mechanics. The quantum region below the threshold is represented by a linear superposition of up- and down-spin states and above it, by a classical up or down spin, but not both simultaneously. It is the states of photon pulses that change a CIM from quantum to classical, allowing for reading out final answers with high accuracy [2]. Regarding the MFB-CIM, following the OPO’s generation of two photons, an optical beam splitter creates a quantum correlation between the internal and external (measured) fields. The use of homodyne detection, which extracts information encoded as an amplitude of an external signal field, induces state reduction for the internal field [3]. (The measurement of a quantum system induces, via “wave-function collapse”, a completely new state.) In the ODL-CIM, optical mutual coupling creates the quantum correlation (entanglement) among OPOs, while in the MFB-CIM, the original quantum correlation is converted to classical correlation among OPOs via measurement feedback. The difference between the two CIMs, which both involve quantum-to-classical transitions, is that the separation or breaking of symmetry occurs through quantum correlation for the ODL-CIM and classical correlation for the MFB-CIM. The two machines also have different histories and tradeoffs. The CIM was originally demonstrated using an ODL, but for the past five years, MFB has predominated. While an ODL is more difficult to implement, once set up, it promises higher operational speed and lower energy consumption.
4. CIM performanceHow has a CIM performed to date? Two tests, one experimental and the other mathematical, indicate a CIM’s unique computational power. In a 2019 benchmark study between the MFB-CIM and QA [4], the success probability (time to solution) of this CIM outperformed QA by an ever-widening gap as the problem size increased. For a dense Max-Cut problem of N = 55, for instance, the MFB-CIM determined a solution seven orders of magnitude faster than did QA from D-Wave, Inc. For a problem size of 100, the differential was estimated as 21 orders of magnitude. These extremely large differentials derive from design. Whereas the MFB-CIM had all-to-all connections among its 2000 spins, QA was connected only locally. This resulted in a divergence in the number of spin-spin couplings: 4 million (CIM) vs. 8 thousand (QA). Ultimately, the difference can be traced back to the basic hardware platforms. QA consists of localized spins and requires real wiring to connect qubits (the basic unit of quantum information). By contrast, a CIM is based on a de-localized harmonic oscillator field, in which mutual spin coupling can be implemented at any place in the machine. In a mathematical comparison with an ideal QC machine [5], the MFB-CIM also outperformed it. In this comparison, the ideal QC exhibited no decoherence, no energy dissipation, no gate error, and all-to-all qubit coupling—conditions that are far from being actualized. Even so, the time-to-solution (TTS) for discrete adiabatic quantum computation (dAQC) and the Grover search, an optimum quantum algorithm for unstructured search, fell far behind. The TTS for Grover search and dAQC scaled in accordance with the exponential of problem size n, and the TTS for the MFB-CIM scaled in accordance with the sub-exponential of n, an increasingly small number. In this case, system design again matters. The unitary QC machines are limited to linear amplitude amplification at best, while a dissipative CIM can increase in this regard exponentially. It can do so because the operating principle of the quantum-to-classical transition enables the stimulated emission of photons above the OPO threshold. In the latest numerical simulation study [6, 7], the CIM with amplitude error correction feedback can be competitive also against state-of-the-art digital heuristics such as Breakout Local Search (BLS) and Simulated Bifurcation Machine (SBM). 5. Future research agendaNotwithstanding the strong results from CIM prototypes and mathematical studies, there remains much from a theoretical perspective to understand about how they perform. This situation contrasts with the prevailing scenario in the QC domain, where experimental results lag far behind the theory. To remedy this knowledge deficit, NTT Research launched an ambitious, long-range collaborative exercise with 14 institutions: Stanford University, California Institute of Technology, The University of Chicago, Cornell University, Harvard University, University of Michigan, Massachusetts Institute of Technology (MIT), NASA Ames Research Center, University of Notre Dame, Swinburne University of Technology, Tokyo Institute of Technology, The University of Tokyo, University of Waterloo, and 1QBit. These joint research projects with 25 principal investigators cover a wide range of topics, including quantum optics and information, neural network and brain science, nonlinear photonics, combinatorial optimization, and machine learning. To be on the edge of new knowledge can be exhilarating. First, there are pressing, real-world problems that a CIM could solve in areas such as operations and scheduling, drug discovery, wireless communications, finance, integrated circuit design, compressed sensing, and machine learning. Then there is the range of interdisciplinary viewpoints that impinge upon this research, which arguably amount to a new field of study. Neuroscience may be one of the most significant of these areas of knowledge. Compared with the static nature of the long-standing legacy computing model, the new paradigm, which includes CIMs, is shifting toward more brain-like functionality, a point captured in our PHI Lab slogan: “Quantum Physics meets Brain Science on Optical Platform.” References
|
|||||||||||||||