Feature Articles: Adapting to the Changing Present and Creating a Sustainable Future
Vol. 20, No. 10, pp. 67–76, Oct. 2022. https://doi.org/10.53829/ntr202210fa10
Number Theory and Quantum Physics Based on Symmetry—Themes from Quantum Optics
Masato Wakayama
Abstract
The connection between mathematics and physics has produced many successes over the centuries. Modern mathematics is used, for example, in cosmology, high energy physics, and condensed matter theory. However, the connection between the theoretical study of quantum optics and modern mathematics, which is also necessary for the construction of quantum computers, is not always deep. In this article, I introduce the quantum Rabi model, which is the most fundamental theoretical model in quantum optics, and its relationship with modern mathematics, especially number theory, from the viewpoint of symmetry. I discuss the motivation for my research, how it has progressed, and future plans. I also introduce that mathematical conjectures arising from this study.
Keywords: non-commutative harmonic oscillator, quantum Rabi model, zeta functions
1. Mathematics and mathematical research
The purpose of mathematical research is to enrich mathematics by solving unsolved problems and discovering new problems, as well as by developing new mathematical visions and theories that can be applied to solutions of many problems. Mathematical research also gives rise to applications that are not immediately apparent. For instance, Riemannian geometry, developed in tandem with physicists, is largely independent from applications and is pure mathematics. It is now used, via Einstein’s theory of general relativity, in making GPS (Global Positioning System) highly effective. Using the example of “research on quantum models and number theory from the viewpoint of symmetry” I describe my research motivation, objectives and results, and future goals based on them. The models mentioned in this article are the non-commutative harmonic oscillator (NCHO) [1], quantum Rabi model (QRM), and asymmetric QRM (AQRM) [2, 3].
Mathematics is, in part, an endeavor to understand, in a unified manner, facts that appear to be far apart, which sometimes takes quite long time. For example, there is the application of the discovery in ancient Greece of the infinity of prime numbers and uniqueness of prime factorization to today’s public key cryptography. It took more than 2500 years to understand that mathematical discoveries can be used to maintain secrecy. Also, the structure of the universe is gradually being revealed through non-Euclidean geometry and group theory, which arose out of the human mind. We now know that economic phenomena and the movement of pollen can be understood in the same way since they are due to the mathematical description of Brownian motion, i.e., the development of stochastic analysis. In fact, there is a special value in the clarification of unquestionable affinities between subjects that have long been believed to be unrelated to each other. According to Henri Poincaré, mathematics is the art of identification. As Shin-Ichiro Tomonaga*1 wrote: “What has worked well is experiment, demonstration/proof, and abstraction through mathematics. Abstraction makes it very universal. These are the great strengths of physics.” Mathematical theorems, however, are not invented but discovered. This becomes clear from Kunihiko Kodaira’s view*2 that mathematical research is, using paper and pencil, to dig out mathematical truths that do exist independent from human minds but are hidden.
The symmetry in the title refers to the actions of groups. We may recall the congruence transformation groups of Euclidean planes and spaces and the crystallographic groups familiar from physics and chemistry. Group theory was founded by Évariste Galois, who died in a duel at the age of 20. Before Galois, there were formulas for roots of quadratic, cubic, and quartic equations, and there were efforts to find those for quintic equations. However, what Galois did was to consider the entirety of the substitutions of the roots of an equation (the permutation group) and found from its structure that there is in general no root formula that uses the usual algebraic operations (addition, subtraction, multiplication, division) and application of radicals (square roots, cube roots, etc.) to coefficients of a polynomial when the equation is of fifth degree or higher*3. This is a major paradigm shift. What is the structure? It is related to the strength of the noncommutativity of the group. There is a large difference between putting on a suit after putting on a shirt and putting on a shirt after putting on a suit. I hope this gives an idea of non-commutative operations (actions).
| *1 |
Shin-Ichiro Tomonaga was a Japanese physicist, influential in the development of quantum electrodynamics, work for which he was jointly awarded the Nobel Prize in Physics in 1965 along with Richard Feynman and Julian Schwinger. |
| *2 |
Kunihiko Kodaira was the first Japanese recipient of the Fields Medal. The K3 surface, an important algebraic surface, was named by Andre Weil after three algebraic geometers (Kummer, Kaehler, Kodaira) and the then unexplored mountain K2. In the sixth night of Soseki Natsume’s short story “Ten Nights of Dreams,” there is a description of Unkei (a Japanese sculptor during the Kamakura period; 1150–1223) carving a statue of Nioh (the guardian gods of a temple gate) at the gate of Gokokuji Temple. One of the observers caught sight of Unkei and said, “He is not carving, he is just digging out the Nioh,” which was originally buried in the wood. This is what Kodaira used to explain. Mathematics, which guarantees the reproducibility essential to science through rigorous proofs, is not a natural science that deals with physical nature, but rather a science that works toward the elucidation of mathematical nature. |
| *3 |
This is the beginning of Galois theory. Many mathematicians have become mathematicians because they were exposed to Galois theory. Although we now call it a “solution formula” for quadratic equations in Japan, it used to be called a “root formula,” since a quadratic equation is one of various equations. However, I would like to use “root” with a special meaning because it is indeed a root which has broadened the world of mathematics. |
2. NCHO
Quantum harmonic oscillators are fundamental in quantum theory. Their energies (eigenvalues) are given as half-integers in the standard normalization, and the corresponding eigenstates are Hermitian functions, i.e., given essentially by the Hermite polynomials times 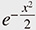 . A clean description of this can be obtained from the representation theory*4 of the three-dimensional Lie algebra . A clean description of this can be obtained from the representation theory*4 of the three-dimensional Lie algebra 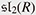 consisting of 2 × 2 matrices with trace 0. The consisting of 2 × 2 matrices with trace 0. The 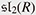 captures the infinitesimal action of the Lie group SL2(R) formed by all real 2 × 2 matrices with determinant 1. Lie group theory originated from the work of Sophus Lie, who was impressed by the Galois theory of algebraic equations and wanted to construct a sort of Galois theory for algebraic differential equations. Lie groups are groups as the name implies and geometric objects called manifolds. In the geometric context, captures the infinitesimal action of the Lie group SL2(R) formed by all real 2 × 2 matrices with determinant 1. Lie group theory originated from the work of Sophus Lie, who was impressed by the Galois theory of algebraic equations and wanted to construct a sort of Galois theory for algebraic differential equations. Lie groups are groups as the name implies and geometric objects called manifolds. In the geometric context, 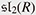 is considered as the tangent space of SL2(R) at the identity element of the group. is considered as the tangent space of SL2(R) at the identity element of the group.
The Hermite functions form a basis of the Hilbert space L2(R) of square integrable functions on the real line. Many special functions, such as Hermite functions, Bessel functions, and Jacobi polynomials, are obtained by specializing one of the parameters a, b, or c of the Gaussian hypergeometric function F(a, b, c; x) to integer values, etc. The differential equation (Gaussian ordinary differential equation (ODE)) satisfied by F(a, b, c; x) has three regular singular points (e.g., 0, 1, ∞). The family of Gaussian hypergeometric functions is indispensable to the number theory of elliptic curves, which has been the flower of mathematics since the 19th century. In representation theory, however, special functions derived from Gaussian hypergeometric functions and its multivariable versions can be understood essentially as matrix elements of representations of Lie groups. I will now turn our attention to the following.
(1) The eigenvalues of (quantum) harmonic oscillators H = a†a + 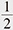 , where a and a† are respectively the creation and annihilation operators subjecting [a†, a] = 1, are half-integers. Therefore, the spectral zeta function*5 of the harmonic oscillator determined from the eigenvalues essentially coincides with the Riemann zeta function ζ(s)*6. , where a and a† are respectively the creation and annihilation operators subjecting [a†, a] = 1, are half-integers. Therefore, the spectral zeta function*5 of the harmonic oscillator determined from the eigenvalues essentially coincides with the Riemann zeta function ζ(s)*6.
(2) The symmetry of SL2(R) remains in the world of Gaussian hypergeometric functions. For instance, the matrix elements of representations of SL2(R) and, almost equivalently, the solution of the SL2(R)-invariant differential equation all can be expressed essentially by Gaussian hypergeometric functions.
The group SL2(R) is behind (1) and (2) above. To explore the wider world, we need to weaken the symmetry. The only noncommutative property of harmonic oscillators is the canonical commutation relation (CCR) controlled by 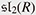 *7. The NCHO*8, which defines a system of ODEs, with two parameters α and β, adds matrix noncommutativity. The name comes from this noncommutativity. Of course, it would not be rational to define it in an arbitrary manner. From expected physical applications and corresponding mathematically reasonable consideration, we thought that it should be at least required that the Hamiltonian *7. The NCHO*8, which defines a system of ODEs, with two parameters α and β, adds matrix noncommutativity. The name comes from this noncommutativity. Of course, it would not be rational to define it in an arbitrary manner. From expected physical applications and corresponding mathematically reasonable consideration, we thought that it should be at least required that the Hamiltonian 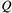 of the NCHO have only real discrete eigenvalues and that it be kept a sufficiently weak symmetry to allow the harmonic oscillator to be recovered when α = β. The former requires that of the NCHO have only real discrete eigenvalues and that it be kept a sufficiently weak symmetry to allow the harmonic oscillator to be recovered when α = β. The former requires that 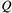 be a positive Hermitian operator (i.e., self-adjoint operator). The latter is that the spectral zeta function ζ be a positive Hermitian operator (i.e., self-adjoint operator). The latter is that the spectral zeta function ζ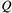 (s) of (s) of  be a good generalization of ζ(s) though neither a functional equation nor Euler product may be expected [4]. be a good generalization of ζ(s) though neither a functional equation nor Euler product may be expected [4].
The convergence region of the defining series of ζ(s) is only in the half-plane, while ζ(s) has analytic continuation to the whole plane. The Riemann Hypothesis*9 asserts that the real part of an imaginary number s with ζ(s) = 0 is always 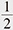 . There are two analogues of the Riemann Hypothesis at the top (and among the best-known achievements) of 20th century mathematics. One is the Weil Conjecture for the congruent zeta function and the other is the Selberg zeta function for the prime geodesic distribution. Both conjectures were settled by the fact that each zeta function has a determinant expression in terms of suitable Hermitian operators*10. The study of a possible determinantal expression of ζ(s) is also important in the attack on the original Riemann Hypothesis. . There are two analogues of the Riemann Hypothesis at the top (and among the best-known achievements) of 20th century mathematics. One is the Weil Conjecture for the congruent zeta function and the other is the Selberg zeta function for the prime geodesic distribution. Both conjectures were settled by the fact that each zeta function has a determinant expression in terms of suitable Hermitian operators*10. The study of a possible determinantal expression of ζ(s) is also important in the attack on the original Riemann Hypothesis.
| *4 |
Representation theory is said to be the study of symmetry. It is at the intersection of algebra, geometry, and analysis, and is indispensable in mathematics that focuses on treating symmetry. In representation theory, each group element is represented by a linear transformation acting on a certain vector space (generally infinite dimensional) and the group product corresponds to composition of these transformations. We use the Weil representation (sometimes called the oscillator representation), the representation of 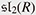 given by the multiplication given by the multiplication 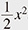 , the differential operator − , the differential operator − 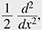 and Euler’s order operator and Euler’s order operator 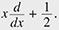 (For an introduction to the Weil representation, see R. Howe and E-C. Tan, “Non-Abelian Harmonic Analysis: Applications of SL(2, R),” Springer, 1992.) (For an introduction to the Weil representation, see R. Howe and E-C. Tan, “Non-Abelian Harmonic Analysis: Applications of SL(2, R),” Springer, 1992.) |
| *5 |
The spectral zeta function of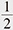 an operator with positive eigenvalues λ1≦λ2≦λ3≦ …, where the multiplicity of the eigenvalue is uniformly bounded, is defined by the Dirichlet series λ1−s+λ2−s+λ3−s+.... an operator with positive eigenvalues λ1≦λ2≦λ3≦ …, where the multiplicity of the eigenvalue is uniformly bounded, is defined by the Dirichlet series λ1−s+λ2−s+λ3−s+.... |
| *6 |
ζ(s): = 1+2−s+3−s+4−s+5−s+…= (1–2−s)−1×(1–3−s)−1×(1–5−s)−1×(1–7−s)−1×(1–11−s)−1 × … (Euler’s product) for a complex number s, the real part of which is greater than 1. The spectral zeta function is in fact identified with (2s − 1)ζ(s). |
| *7 |
Define h = a†a + , e+ = 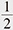 a†2 and e− = − a†2 and e− = − 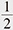 a2, then the triplet {h, e+, e−} forms the Lie algebra a2, then the triplet {h, e+, e−} forms the Lie algebra 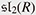 , that is, the commutation relations [h, e±] = ±2e± and [e+, e−] = h hold. Here h = 2H + , that is, the commutation relations [h, e±] = ±2e± and [e+, e−] = h hold. Here h = 2H + 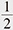 for the Hamiltonian of harmonic oscillator H = for the Hamiltonian of harmonic oscillator H = 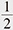 a†a. a†a. |
| *8 |
The Hamiltonian 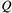 of the NCHO is of the form of the NCHO is of the form 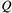 := := 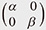 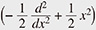 + + 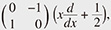 where α and β are positive and αβ > 1. The condition on α and β guarantees that where α and β are positive and αβ > 1. The condition on α and β guarantees that 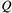 has only positive and discrete eigenvalues with uniformly bounded multiplicity. has only positive and discrete eigenvalues with uniformly bounded multiplicity. |
| *9 |
It is still unsolved more than 160 years after being stated by Riemann (1859). This conjecture, which has been challenged by many geniuses, is equivalent to the ultimate distribution of primes, as shown in 1901 by Helge von Koch. Koch is famous for the Koch snowflake/curve, after whom it is named. |
| *10 |
The congruence determined for smooth algebraic manifolds and schemes over finite fields was positively solved in the case of zeta functions by the determinantal expression of what is called the Frobenius operator, and in the case of Selberg zeta functions by the Laplacian, the (unique up to a constant) invariant differential operator on the complex upper half-plane. |
3. QRM and NCHO
Isidor Isaac Rabi described the interaction of classical light with atomic quantum states in 1936. In 1963, Edwin Jaynes and Fred Cummings quantized light as well and defined the QRM and its rotating wave approximation, now known as the Jaynes-Cummings model. However, while the integrability of the QRM was unknown, the Jaynes-Cummings model was useful because of the existence of continuous invariants, making the theoretical treatment easy, and suitability to experiments if the light-matter coupling is very weak, roughly a fraction 10−6 of the mode frequency*11.
However, with the possibility of developing a quantum computer on circuit quantum electrodynamics (QED) platforms, the weak coupling approximation is no longer justified, and one must use the QRM in the ultra-strong coupling regime. In 2011, Daniel Braak [2] demonstrated the integrability of the QRM, and research on the periphery of the QRM has advanced rapidly since. In fact, the experimental measurement results [5] using superconducting artificial atoms were consistent with the theory of the QRM and its generalization, the AQRM (see also [6]).
The NCHO has expanded the world from Gauss’s as expected. In fact, the eigenvalue problem of the NCHO was found to be equivalent to the existence of holomorphic solution of the Heun ODE*12 in the complex region containing 0, 1, and not including αβ. This fact was discovered by Hiroyuki Ochiai [7] and fully understood 15 years later [8]. The (A)QRM also has a Heun picture [2]. However, unlike the NCHO, it is a confluent Heun differential equation. Nevertheless, by merging the two singularities as αβ → ∞, a confluent Heun picture of the QRM can be obtained from the Heun picture of the NCHO [8]. In other words, the NCHO can be considered as a covering model of the QRM*13 (Fig. 1, the NCHO is a covering model of the QRM).
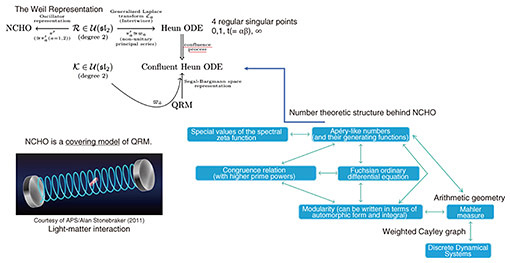
Fig. 1. NCHO & QRM.
Quantization is discretization and passing from a commutative world to a non-commutative world. The former is the original arena of number theory. In fact, the special values of ζ (s) in the NCHO shows rich number theory as I explain below. For instance, as to the special values of the spectral zeta function of the harmonic oscillator, essentially given by ζ(s), there is the old Basel problem to determine the value of the infinite series (s) in the NCHO shows rich number theory as I explain below. For instance, as to the special values of the spectral zeta function of the harmonic oscillator, essentially given by ζ(s), there is the old Basel problem to determine the value of the infinite series 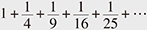 *14, which was solved by Euler. The even integer values of ζ(s) are generally expressed in terms of powers of π and rational numbers. However, the value and properties of ζ(s) at odd points remained unknown for more than 300 years until Roger Apéry’s proof that ζ(3) is irrational in 1978. The best result on irrationality is still the theorem that at least one of ζ(5), ζ(7), ζ(9), or ζ(11) is an irrational number. However, the research on special values is a deep problem in modern mathematics, such as the geometric conjecture on special values of various zeta functions by Pierre Deligne*15 who solved the Weil Conjecture using Grothendieck’s arithmetic geometry, and the Birch-Swinnerton-Dyer conjecture on special values at the central point of L-functions (relatives of zeta) defined from elliptic curves and its generalization by Bloch, Beilinson, and Kato. *14, which was solved by Euler. The even integer values of ζ(s) are generally expressed in terms of powers of π and rational numbers. However, the value and properties of ζ(s) at odd points remained unknown for more than 300 years until Roger Apéry’s proof that ζ(3) is irrational in 1978. The best result on irrationality is still the theorem that at least one of ζ(5), ζ(7), ζ(9), or ζ(11) is an irrational number. However, the research on special values is a deep problem in modern mathematics, such as the geometric conjecture on special values of various zeta functions by Pierre Deligne*15 who solved the Weil Conjecture using Grothendieck’s arithmetic geometry, and the Birch-Swinnerton-Dyer conjecture on special values at the central point of L-functions (relatives of zeta) defined from elliptic curves and its generalization by Bloch, Beilinson, and Kato.
Apéry used a sequence of rational numbers, now called the Apéry numbers, to prove the impossibility that ζ(3) is rational. Frits Beukers took up the challenge of finding out why and further proving irrationality and developed a brilliant study of elliptic curves, K3 surfaces, and automorphic forms behind the proof of the irrationality [9]. As a result, he showed remarkable congruence relations of the Apéry numbers, which have become the subject of research in algebraic number theory. Surprisingly, the special values ζ (2) and ζ (2) and ζ (3) for the NCHO also yield sequences of numbers with properties like those of the Apéry numbers [10, 11, 12]. Elliptic curves and automorphic forms underlie these properties, and when s = 4, even automorphic integrals*16, which generalize the notion of automorphic forms, appear [10] via certain nearly holomorphic automorphic forms initially studied by Goro Shimura*17. The next development will be the study of a wider range/class of automorphic forms (also related to the Langlands program, which is extremely important in mathematics [13]). (3) for the NCHO also yield sequences of numbers with properties like those of the Apéry numbers [10, 11, 12]. Elliptic curves and automorphic forms underlie these properties, and when s = 4, even automorphic integrals*16, which generalize the notion of automorphic forms, appear [10] via certain nearly holomorphic automorphic forms initially studied by Goro Shimura*17. The next development will be the study of a wider range/class of automorphic forms (also related to the Langlands program, which is extremely important in mathematics [13]).
| *11 |
The Nobel Prize in Physics 2012 awarded to Serge Haroche and David J. Wineland for their groundbreaking experimental method for the measurement and manipulation of quantum systems seems to be at the center of this trend. |
| *12 |
The Heun equation is a second-order ODE of Fuchsian type with four fixed singular points, e.g., (0, 1, t, ∞). Unlike Gaussian hypergeometric functions, there are aspects of its mathematical structure that need to be clarified, but they appear in the description of various physical phenomena. The Gaussian hypergeometric equation can be considered a degenerate case of the Heun equation. This is the first meaning for expanding the world from Gauss’s. |
| *13 |
This is also true for the AQRM by adding an appropriate shifted (biased) term to the NCHO. |
| *14 |
In terms of the special value of ζ(s), 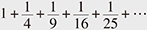 = ζ(2) = = ζ(2) = 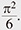 The appearance of π was a great surprise. The appearance of π was a great surprise. |
| *15 |
Fields Medal 1978. |
| *16 |
Also called the Eichler form. |
| *17 |
This fact means that the second reason we can expand the world from Gauss’s. The notion of automorphic integrals (sometimes called Eichler’s forms) appeared in [10] is a further reasonable extension of the standard one. |
4. Spectra of the AQRM and hidden symmetries
The importance of the partition function (weighted sum of states) in statistical mechanics is that it encodes the time evolution of the system. Knowing the exact behavior of a quantum system during a long period is of utmost importance to any task in quantum computing. Purely numerical approaches are severely limited due to the accumulation of rounding errors in the long-time limit. Therefore, it is necessary to derive analytical formulas for its heat kernel and partition function. In fact, the partition function and spectral zeta function have a one-to-one correspondence through the Mellin integral transform. However, obtaining these analytical formulas was considered extremely difficult. Physicists use a highly intuitive form of expression called Feynman path integral to carry out various asymptotic or approximate (as well as precise) calculations to gain a better understanding of the physical system of interest. The translation invariant measure and integral on the space of paths cannot be treated mathematically in a rigorous manner, except in some special cases. Of course, various studies are still ongoing to understand it. I, together with Reyes-Bustos, have attempted to derive a heat kernel for the (A)QRM*18. The method, which has been successfully applied [14], is based on the action of the symmetric group  of the mth order on of the mth order on 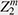 (m = 1,2,...), the Fourier transform on (m = 1,2,...), the Fourier transform on 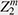 *19, and graph theory, where Z2 is Z/2Z or the field of two elements F2 = {0,1}. The resulting analytic formula is practically given by the series over non-negative integers m for integrals over m-simplex (an m-fold integral) of elementary functions given by products and quotients of exponential functions. It can also be interpreted as the infinite sum (integral) of the orbit integrals of *19, and graph theory, where Z2 is Z/2Z or the field of two elements F2 = {0,1}. The resulting analytic formula is practically given by the series over non-negative integers m for integrals over m-simplex (an m-fold integral) of elementary functions given by products and quotients of exponential functions. It can also be interpreted as the infinite sum (integral) of the orbit integrals of 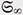 over the entire equivalence class by the infinite symmetric group over the entire equivalence class by the infinite symmetric group 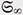 of discrete paths connecting 0 and ∞ (Fig. 2, Discrete paths and infinite symmetry groups (Geometric Interpretation)). From a representation theoretic point of view, the action of of discrete paths connecting 0 and ∞ (Fig. 2, Discrete paths and infinite symmetry groups (Geometric Interpretation)). From a representation theoretic point of view, the action of 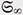 on on 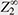 corresponds to a decomposition into the direct sum of irreducible representations (Fig. 3 (Algebraic Interpretation)). The formulas obtained are similar to formulas for partition functions obtained for the spin-boson model or the Kondo model (describing magnetic impurities in non-magnetic host metals, named after Jun Kondo, 1930–2022), a formally exact description of the matrix element of the heat kernel, and to approximate partition functions for various physical systems. For a general model, the (possible) existence of an infinite-dimensional algebraic system acting on the non-countable paths of the Feynman integrals and the acquisition of discrete paths as their equivalence analogue should also be pursued (Fig. 4, Conjecture on the paths of the Feynman path integral). corresponds to a decomposition into the direct sum of irreducible representations (Fig. 3 (Algebraic Interpretation)). The formulas obtained are similar to formulas for partition functions obtained for the spin-boson model or the Kondo model (describing magnetic impurities in non-magnetic host metals, named after Jun Kondo, 1930–2022), a formally exact description of the matrix element of the heat kernel, and to approximate partition functions for various physical systems. For a general model, the (possible) existence of an infinite-dimensional algebraic system acting on the non-countable paths of the Feynman integrals and the acquisition of discrete paths as their equivalence analogue should also be pursued (Fig. 4, Conjecture on the paths of the Feynman path integral).
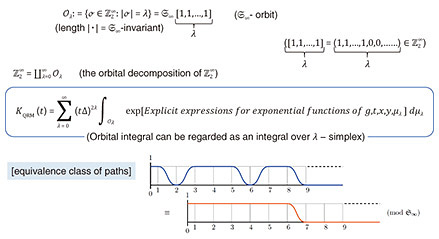
Fig. 2. Heat Kernel Formula °› Geometrical Interpretation.
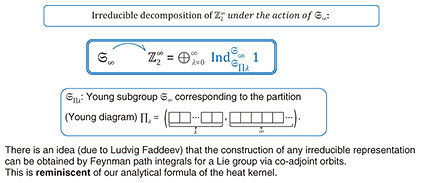
Fig. 3. Heat Kernel Formula °› Algebraic (Group Theoretic) Interpretation.
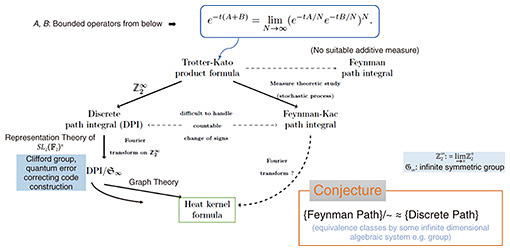
Fig. 4. Product Formulas of Trotter-Kato  Heat Kernel, Propagator. Heat Kernel, Propagator.
From the analytical formula for the heat kernel, the partition function is obtained, and the contour integral expression of the spectral zeta function is gained*20. Thus, the analytic connection to the whole plane is obtained, the asymptotic evaluation of the number of eigenvalues (Weyl’s law) follows, and we can start the special value study [15]. What is the number theory and geometric structure of the QRMs? This is one of the most important questions in this area.
The AQRM is of major importance in circuit QED implementations of the QRM, thus for applications to quantum computing. Unlike the QRM, it has no visible Z2-symmetry (parity), if the bias is not zero. Nevertheless, it shows characteristic spectral degeneracies at half-integer values of the bias parameter. In fact, the AQRM is degenerate if and only if the bias parameter (of the bias operator) of the Hamiltonian*21 is a half-integer ℓ/2 (ℓ ∈ Z) [3, 16]. In physics, however, degeneracy is considered to indicate the existence of a symmetry [17]. Unlike classical mechanics, the concept of integrability is not clear in quantum mechanics [18]. However, the analogy with classical systems has led to the search for operators that commute with HAQRM but are not functions of HAQRM, indicating the presence of an additional conserved quantity [19]. Inspired by this study, we [20] conducted a thorough analysis to completely determine the operators that are commuting with the HAQRM. Interestingly, the ring*22 of operators commuting with HAQRM, has a unique natural generator Jℓ up to a constant multiple. Moreover, the square of Jℓ is expressed as Jℓ2 = pℓ (HAQRM, g, Δ), a polynomial in HAQRM, where pℓ is an ℓth degree polynomial. The equation y2 = pℓ (x; g, Δ) defines a hyperelliptic curve [21].
On the other hand, the degenerate eigenvalues of the AQRM are of the form N ± 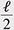 + g2 with positive integer N. Fixing N and ℓ, (g2, Δ2) is obtained as zeros of the constraint polynomial + g2 with positive integer N. Fixing N and ℓ, (g2, Δ2) is obtained as zeros of the constraint polynomial 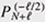 (g2, Δ2) and (g2, Δ2) and 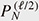 (g2, Δ2) [12]. In fact, (g2, Δ2) [12]. In fact, 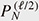 (g2, Δ2) divides (g2, Δ2) divides 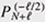 (g2, Δ2), and the quotient polynomial is (g2, Δ2), and the quotient polynomial is 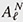 (g2, Δ2) (>0) [16]. It should also be noted that the AQRM degeneracies are, geometrically, conical intersection points in the three-dimensional spectral graph (Left of Fig. 5). (g2, Δ2) (>0) [16]. It should also be noted that the AQRM degeneracies are, geometrically, conical intersection points in the three-dimensional spectral graph (Left of Fig. 5).
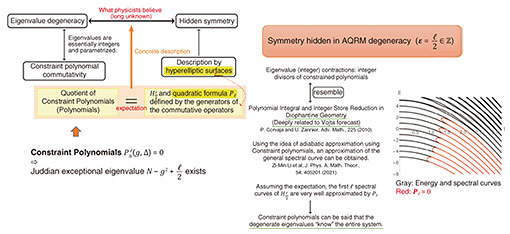
Fig. 5. Clarification of the underlying fundamental reason is expected.
From experimental calculations, we know that 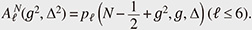 If this holds in general, the expectation “hidden symmetry behind the degeneracy” becomes explainable concretely provided we may think of the existence of a non-trivial operator commuting with the Hamiltonian (which is in fact an involution modulo the Hamiltonian) as evidence of quantum integrability*23 (Fig. 5 and Fig. 6). There is, however, no way to prove it, and it remains a conjecture [21]. However, this conjecture is very similar in form to a certain theorem*24 in the Diophantine geometry*25 [22] in its form. Therefore, a clue to the proof might be found there. We also expect that the AQRM has a finite number of degenerate eigenvalues for fixed parameters g and Δ. Although it is still unresolved, we can find some formal similarities with the Mordell Conjecture*26 in this case. If this holds in general, the expectation “hidden symmetry behind the degeneracy” becomes explainable concretely provided we may think of the existence of a non-trivial operator commuting with the Hamiltonian (which is in fact an involution modulo the Hamiltonian) as evidence of quantum integrability*23 (Fig. 5 and Fig. 6). There is, however, no way to prove it, and it remains a conjecture [21]. However, this conjecture is very similar in form to a certain theorem*24 in the Diophantine geometry*25 [22] in its form. Therefore, a clue to the proof might be found there. We also expect that the AQRM has a finite number of degenerate eigenvalues for fixed parameters g and Δ. Although it is still unresolved, we can find some formal similarities with the Mordell Conjecture*26 in this case.
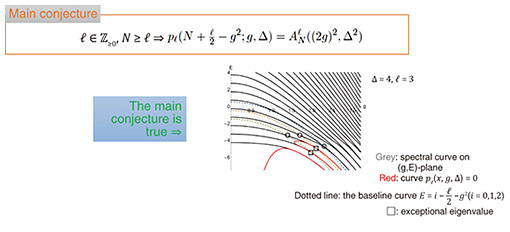
Fig. 6. The degenerate eigenvalues may “know” the entire spectrum of the system.
| *18 |
The Trotter-Kato product formula is the starting point for the heat kernel derivation; it is useful to derive the Feynman path integral formally, or even considered as the rigorous description of the Feynman path integral. |
| *19 |
It is a part of the action of the oscillator representation of SL2(F2)n. This representation is used for the construction of quantum error correcting codes such as Clifford cord. |
| *20 |
The contour integral is a path starting from the infinity point ∞, circling around the origin 0, and returning to ∞. |
| *21 |
The AQRM Hamiltonian has the form HAQRM = a†a [photon field] + 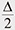 σz [two-level atom] + g(a + a†) σx [interaction term] + ϵσx [bias term (given by a real number)], where σ* is Pauli matrix, Δ is the energy difference of the two level atom and g the coupling (interaction) constant. We notice that the bias term given by ϵ ∈R of HQRM is zero. Note that after its proposal in [2], the AQRM (as it is now called) was called the “generalized” QRM, “biased” QRM, “driven” QRM, etc., but after [3], “asymmetric” QRM became established. σz [two-level atom] + g(a + a†) σx [interaction term] + ϵσx [bias term (given by a real number)], where σ* is Pauli matrix, Δ is the energy difference of the two level atom and g the coupling (interaction) constant. We notice that the bias term given by ϵ ∈R of HQRM is zero. Note that after its proposal in [2], the AQRM (as it is now called) was called the “generalized” QRM, “biased” QRM, “driven” QRM, etc., but after [3], “asymmetric” QRM became established. |
| *22 |
It is an algebraic system closed in addition and multiplication except for division, such as the whole of integers (integer ring) and the whole of polynomials (polynomial ring). |
| *23 |
We can define a new mathematical model that we call the shifted NCHO. This model gives the covering model of the AQRM by looking at each Heun ODE picture for the shifted NCHO and AQRM, respectively. Since the model keeps the apparent parity symmetry at the Hamiltonian level, the hidden symmetry of the AQRM may also be explained as the inheritance of this parity symmetry. |
| *24 |
This theorem is closely related to the well-known Vojta Conjecture. The Vojta Conjecture is also a higher dimensional version of the Mordell Conjecture and closely related to the ABC Conjecture. |
| *25 |
A fundamental theme in number theory concerns the study of integer and rational solutions to Diophantine equations (polynomial equations). This topic originated at least 3,700 years ago as documented in Babylonian clay tablets. There are interesting interactions between Diophantine Geometry and several fields such as representation theory, algebraic geometry, topology, complex analysis, and mathematical logic, to mention a few, which have been found to be quite fruitful. |
| *26 |
The conjecture that a curve with a number of holes (genus) greater than 1 defined on a rational number field would have only a finite number of rational points, proved by Gerd Faltings in 1983. |
5. Conclusion
Let us discuss a few phrases that characterize mathematics. First, “All things are numbers” by Pythagoras. This is reminiscent of the big data and artificial intelligence (AI) that dominate modern society. The genius Leonardo da Vinci said, “Engineering is the paradise of the mathematical sciences. After all, it is here that the fruits of mathematics are borne.” Galileo Galilei’s “The universe is written in mathematical language” is well known. Wigner’s “The unreasonable effectiveness of mathematics in the natural sciences,”*27 is a brilliant point.
Although mathematical research is like musical composition in some respects, it has been difficult to find a mechanism to make mathematical papers play like music, such as reproducing a symphony from a score. However, the use of mathematics has emerged because of machine learning, AI, and other technologies. Although the motivations for research are diverse, including pure mathematics driven solely by curiosity, it now seems as if an opportunity has arrived for basic mathematics and applied mathematics to play a brilliant concerto. I close this article with the hope that a new “mathematical music” (in Japanese, we may express it as  (su-gaku) meaning enjoining mathematics and is a homonym with (su-gaku) meaning enjoining mathematics and is a homonym with  (su-gaku) meaning the study of numbers, i.e., mathematics)*28. (su-gaku) meaning the study of numbers, i.e., mathematics)*28.
| *27 |
The following is an excerpt from a lecture transcript published in 1960 by Eugene Wigner (1902–1995: Nobel Prize in Physics 1963, “Discovery of Symmetry in the Theory of Nuclei and Elementary Particles”). Wigner°«s remark echoes a well-known sentence by Einstein, who said, “Das ewig Unbegreifliche an der Welt ist ihre Begreiflichkeit.” in English: “The fact that the universe is comprehensible [by mathematical means] is utterly incomprehensible.” |
| *28 |
Many professions in academia, e.g., scientist, physicist, chemist, and linguist end in “st.” However, astronomer and geometer end in “er.” Magician, musician, and mathematician end in “cian,” and their initial letter is “m.” Perhaps there might be some influence of liberal arts education (the seven liberal arts) dating back to ancient Greece and Rome, but it is not easy to explain immediately. It is just interesting to notice. |
References
| [1] |
A. Parmeggiani and M. Wakayama, “Oscillator Representations and Systems of Ordinary Differential Equations,” PNAS, Vol. 98, pp. 26–30, 2001. |
| [2] |
D. Braak, “Integrability of the Rabi Model,” Phys. Rev. Lett., Vol. 107, 100401, 2011. |
| [3] |
M. Wakayama, “Symmetry of Asymmetric Quantum Rabi Models,” J. Phys. A: Math. Theo., Vol. 50, pp. 174001–174020, 2017. |
| [4] |
T. Ichinose and M. Wakayama, “Zeta Functions for the Spectrum of the Non-commutative Harmonic Oscillators,” Comm. Math. Phys., Vol. 258, pp. 697–739, 2005. |
| [5] |
F. Yoshihara, T. Fuse, Z. Ao, S. Ashhab, K. Kakuyanagi, S. Saito, T. Aoki, K. Koshino, and K. Semba, “Inversion of Qubit Energy Levels in Qubit-oscillator Circuits in the Deep-strong-coupling Regime,” Phys. Rev. Lett., Vol. 120, 183601, 2018. |
| [6] |
M. Wakayama, “Quantum Interaction and Special Values of Zeta Functions,” Sugaku Tsushin, Math. Soc. Japan., Vol. 25, No. 4, pp. 24–52, 2021 (in Japanese). |
| [7] |
H. Ochiai, “Non-commutative Harmonic Oscillators and Fuchsian Ordinary Differential Operators,” Comm. Math. Phys., Vol. 217, pp. 357–373, 2001. |
| [8] |
M. Wakayama, “Equivalence between the Eigenvalue Problem of Non-commutative Harmonic Oscillators and Existence of Holomorphic Solutions of Heun Differential Equations, Eigenstates Degeneration, and the Rabi Model,” Int. Math. Res. Not., Vol. 145, pp. 759–794, 2016. |
| [9] |
F. Beukers, “Irrationality of π2, Periods of an Elliptic Curve and Γ1 (5),” Diophantine Approximations and Transcendental Numbers (Luminy, 1982), Progr. Math., Vol. 31, pp. 47–66, 1983. |
| [10] |
K. Kimoto and M. Wakayama, “Apéry-like Numbers for Non-commutative Harmonic Oscillators and Automorphic Integrals,” Ann. Inst. Henri Poincaré D (to appear), arXiv:1905.01775, 2019. |
| [11] |
L. Long, R. Osburn, and H. Swisher, “On a Conjecture of Kimoto and Wakayama,” Proc. Amer. Math. Soc., Vol. 144, No. 10, pp. 4319–4327, 2016. |
| [12] |
J.-C. Liu, “A Generalized Supercongruence of Kimoto and Wakayama,” J. Math. Anal. Appl., Vol. 467, No. 1, pp. 15–25, 2018. |
| [13] |
R. Langlands, “Letter to André Weil,”
https://publications.ias.edu/rpl/paper/43 |
| [14] |
C. Reyes-Bustos and M. Wakayama, “The Heat Kernel for the Quantum Rabi Model,” Adv. Theor. Math. Phys. (to appear), arXiv:1906.09597, 2020. |
| [15] |
C. Reyes-Bustos and M. Wakayama, “Heat Kernel for the Quantum Rabi Model: II. Propagators and Spectral Determinants,” J. Phys. A: Math. Theor., Vol. 54, pp. 115202–115231, 2021. |
| [16] |
K. Kimoto, C. Reyes-Bustos, and M. Wakayama, “Determinant Expressions of Constraint Polynomials and the Spectrum of the Asymmetric Quantum Rabi Model,” Int. Math. Res. Not., Vol. 2021, No. 12, pp. 9458–9544, 2021. |
| [17] |
S. Ashhab, “Attempt to Find the Hidden Symmetry in the Asymmetric Quantum Rabi Model,” Phys. Rev. A, Vol. 101, 023808, 2020. |
| [18] |
J. S. Caux and J. Mossel, “Remarks on the Notion of Quantum Integrability,” J. Stat. Mech., 02023, 2011. |
| [19] |
V. Mangazeev, M. Batchelor, and V. Bazhanov, “The Hidden Symmetry of the Asymmetric Quantum Rabi Model,” J. Phys. A: Math. Theor., Vol. 54, 12LT01, 2021. |
| [20] |
C. Reyes-Bustos, D. Braak, and M. Wakayama, “Remarks on the Hidden Symmetry of the Asymmetric Quantum Rabi Model,” J. Phys. A: Math. Theor., Vol. 54, pp. 285202–285215, 2021. |
| [21] |
C. Reyes-Bustos and M. Wakayama, “Degeneracy and Hidden Symmetry for the Asymmetric Quantum Rabi Model with Integer Bias,” Commun. Number Theor. Phys. (to appear), arXiv:2106.08916, 2021. |
| [22] |
P. Corvaja and U. Zannier, “Integral Points, Divisibility between Values of Polynomials and Entire Curves on Surfaces,” Adv. Math., Vol. 225, pp. 1095–1118, 2010. |
 |
- Masato Wakayama
- Head and Fundamental Mathematics Research Principal of NTT Institute for Fundamental Mathematics.
He graduated from Tokyo University of Science in 1978 and completed a doctoral course at Hiroshima University°«s Graduate School of Science in 1985 (Doctor of Science). Before becoming a research principal at NTT Institute for Fundamental Mathematics on October 1, 2021, he had held many other academic positions: an associate professor at Tottori University and Kyushu University, visiting fellow at the Department of Mathematics, Princeton University, visiting professor at the University of Bologna, distinguished lecturer at Indiana University (Bloomington), distinguished professor in Mathematics, Dean of the Graduate School of Mathematics, Kyushu University, the first director of the Institute of Mathematics for Industry, executive vice president of Kyushu University, and vice president and professor of Tokyo University of Science. He is also a principal fellow of CRDS (Center for Research and Development Strategy, Japan Science and Technology Agency), and a professor emeritus of Kyushu University. He specializes in representation theory, number theory, and mathematical physics.
|
↑ TOP
|








