|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
Feature Articles: The Forefront of Cryptography Research with an Eye on the Quantum Era Vol. 21, No. 7, pp. 43–47, July 2023. https://doi.org/10.53829/ntr202307fa4 Security of Hash Functions against Attacks Using Quantum ComputersAbstractSHA-2 is a cryptographic hash function used worldwide. The possibility of attacks that exploit quantum computers can no longer be ignored; therefore, it is necessary to verify how the emergence of quantum computers could affect the security of SHA-2. The results of research conducted by my colleague and I indicate—as a world’s first—that in a world in which quantum computers are available, the number of breakable steps in a collision attack on SHA-2 will increase. Keywords: cryptographic hash function, SHA-2, quantum algorithm 1. Introduction to SHA-2If a large-scale, general-purpose quantum computer becomes available for practical use, a malicious attacker could use it to break cryptosystems. To prepare for such attacks, it is necessary to verify the extent to which conventional cryptographic schemes can withstand them. SHA-2 is one of the most-important cryptographic hash functions. It is standardized by the National Institute of Standards and Technology (NIST) and used unsuspectedly by users browsing websites on their personal computers and smartphones in a manner that supports the advanced information society from behind the scenes. Although hash functions are not ciphers, they are used as parts of various other cryptographic techniques and closely related to the security attained with such techniques*1. The main role of a cipher is to encrypt a message and write its content. It of course must be possible to restore the ciphertext (by using a private key) to the original message. In contrast, the role of a hash function (represented as “h”) such as SHA-2 is to receive a message M as input and output a random value, h(M), in a manner that does not hide the content of M. A pair of separate messages, M and M’, that satisfy h(M)=h(M’) is called a collision, and a secure hash function must be able to withstand (i.e., be collision-resistant) attacks that attempt to discover collisions (Table 1).
When we consider collision attacks, we assume that an attacker is given a hash function h*2 and simply wants to find M and M’ that satisfy h(M)=h(M’). Therefore, a collision attack is slightly different from cryptanalyzing ciphers, which is an attack that attempts to recover the original message given the ciphertext encrypted with a cipher. The extent to which a collision attack can be withstood is limited. An important concept that explains this limitation is the birthday paradox*3. An attack applying this concept (birthday attack) finds a collision of an arbitrary hash function with time complexity 2n/2 if the length of outputs is n-bit. A birthday attack is a generic attack that can be applied regardless of the degree of security of the hash function. This, in turn, means that a secure hash function must resist collision attacks (using classical computers) with time complexity less than 2n/2. For example, if a dedicated attack finds a collision of a certain hash function with computational complexity of less than 2n/2, it is considered that the hash function has a unique weakness and has been broken. In other words, computational complexity 2n/2 of a birthday attack is the criterion for judging whether a dedicated attack targeting a specific hash function is a meaningful one.
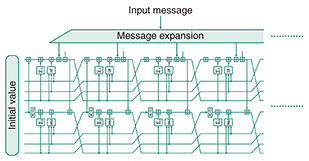
2. Security indicators of SHA-2The mechanism by which SHA-2 calculates the output is explained as follows. First, the input data are expanded into message blocks. Each message block is used to update the value of the internal state. With an initial value as the start point, the final output (hash value) is computed by repeatedly updating the internal state many times by using the message blocks (Fig. 1).
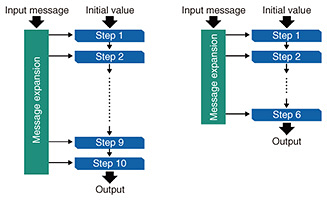
The design of typical hash functions, including SHA-2, involves many iterations of similar operations, and, as the number of iterations decreases, the hash function generally becomes less secure. Accordingly, the measure of security is based on the idea to what extent the hash function can be weakened to the point where it can be broken. For example, suppose that the original hash function is configured as ten iteration steps (Fig. 2, left) and it is known that if the number of steps is reduced to six, it is possible to find a collision with computational complexity less than 2n/2. Then, it is said that the reduced (six-step) version of the hash function is broken (Fig. 2, right). A hash function is considered broken when the original function without step reductions is broken. Even if the number of attacked steps has not reached the original number, an attack can be considered a meaningful attack if the number of broken steps is increased.
When a hash function carefully designed by a professional is broken, the number of broken iterations gradually increases. It is rare that the original function suddenly breaks. The fact that researchers from all over the world have tried to attack SHA-2 but only considerably weakened versions are broken ensures the security of the hash function. 3. Can quantum computers even promptly break hash functions?Since hash functions such as SHA-2 do not have a neat algebraic structure like that of prime factorization, it has been thought that they would not be immediately breakable with the advent of quantum computers. It has been shown that the computational complexity of the generic collision attack*4 fell from 2n/2 of the birthday attack to 2n/3 (i.e., that of the Brassard–Høyer–Tapp (BHT) algorithm). However, the reduction in computational complexity is not so large, so it is accepted that it poses no particular problem as long as a hash function with a slightly larger n is used. However, as research progressed, it became clear that the situation was not so simple. First, as shown in Table 2, it was shown that hash functions, such as Advanced Encryption Standard Matyas–Meyer–Oseas (AES-MMO) and Whirlpool, can be broken by quantum computers in one more iteration, namely, one more step than in the case of classical computers. Quantum computers are clearly more capable of breaking hitherto robust cryptography than classical computers [2].
The increase in the number of breakable steps is based on the idea that while the computational complexity of generic collision attacks does not decrease significantly, the computational complexity of dedicated attacks that target specific hash functions may decrease to a greater degree, so the power of dedicated attacks may increase relatively. For example, when a quantum algorithm called Grover’s algorithm is used for attacks, the computational complexity of differential cryptanalysis, which is often used for dedicated attacks, could fall to about the square root of the original [3]. On the contrary, it has been proven that the computational complexity of a generic collision attack does not fall below that of the BHT algorithm, and the degree of decrease in computational complexity does not reach the square root of the original (Table 3).
As described above, one (classical) measure of security of a hash function is how many steps must be removed to break the function. The effectiveness of a dedicated attack on a hash function that has been reduced to a specific number of steps was determined by whether the computational complexity of the attack was less than that of the generic attack. In a world where quantum computers are available, the computational complexity of a generic attack, which should be the criterion for determining whether the attack is successful, does not change much. In comparison, the speed-up for dedicated attacks by quantum computers is relatively greater. It must therefore be concluded that there are more types of dedicated attacks judged to be more effective in the quantum world than in the classical world. By carefully investigating such a criterion under the assumption that quantum computers are available, collision attacks on 7-stage AES-MMO and 6-stage Whirlpool turned out to be effective in a world where quantum computers are available, even though they were not judged effective in the classical sense. These attacks are concrete examples demonstrating the importance of the aforementioned viewpoint.
4. Attacks on SHA-2 by quantum computersHash functions such as AES-MMO and Whirlpool are, however, minor compared to SHA-2, and their usage scenarios are relatively limited. That situation naturally raises the question of whether the number of breakable steps of SHA-2, i.e., the most widely used hash function today, is increased if quantum computers are available. This question is the main theme of this report. We eventually found that the number of breakable steps can be increased as expected. SHA-2 is a generic term that includes several functions with different output lengths such as SHA-256 and SHA-512, and we found collision attacks on SHA-256 and SHA-512 that are classically ineffective but judged effective in a world with quantum computers [4]. If a classical computer is used, the collision resistance of SHA-256 is broken when the number of steps is reduced to 31, while the original number of steps is 64. However, no attacks were found that would break collision resistance when more than 31 steps were iterated. We found that, in a world where quantum computers are available, collision resistance is broken even after 38 steps. It can thus be said that quantum computers degrade the security of SHA-2, and we obtained a similar result on the security of SHA-512 (Table 4).
Of course, this result does not immediately indicate that the collision resistance of SHA-2 has been broken. SHA-2 is still safe to use. However, the above-mentioned results clearly indicate that the traditional broad view that quantum computers may not have much impact on the security of SHA-2 should be reconsidered. 5. Future developmentsIn a short period, information and communication technology (ICT) has made rapid progress, and in conjunction with that progress, cryptographic technology, which is the cornerstone of security, has become firmly established. Consequently, international-standard cryptographic techniques that can be used by anyone across the world*5 have been established. However, there are many research questions yet to be investigated, especially when it comes to security against attacks using quantum computers. Even the security of SHA-2, which plays a vital role in society, is not well understood. To address this lack of understanding, we conclude that in a world where quantum computers are available, the number of breakable steps in a collision attack on SHA-2 will increase. We must continue to search for unknown attacks. Feedback from the study of these attacks will help us design more-secure hash functions in the future. Moreover, we believe that the publication of the results of such research on attacks will further enhance the security of ICT worldwide. Since an attacker may already be secretly conducting similar research, the goal is to anticipate further attacks by quantum computers and create cryptosystems that can sufficiently withstand them. It may be difficult to grasp the reality of these issues because they are of a dimension different from that of our daily lives. Regardless, as quantum computers come into practical use, it will be necessary to consider these issues before attackers do. A dedicated attack targeting a specific cryptographic technique exploits the internal structure of the technique, so it is not necessarily applicable to other research. Even so, since the security of cryptography is closely related to our daily lives, we expect it to be of broad interest.
References
|
|||||||||||||||||||||||