|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
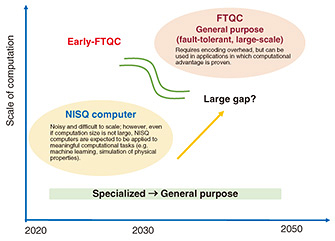
Feature Articles: Efforts to Speed Up Practical Application of Quantum Computers Vol. 21, No. 11, pp. 43–48, Nov. 2023. https://doi.org/10.53829/ntr202311fa5 Toward Early Fault-tolerant Quantum ComputingAbstractThis article introduces new approaches to develop early fault-tolerant quantum computing (early-FTQC) such as improving efficiency of quantum computation on encoded data, new circuit efficiency techniques for quantum algorithms, and combining error-mitigation techniques with fault-tolerant quantum computation. Keywords: quantum computer, fault-tolerant quantum computation, early fault-tolerant quantum computing 1. Noisy intermediate-scale quantum computers and fault-tolerant quantum computersNoisy intermediate-scale quantum (NISQ) computers, which do not execute quantum error correction, do not require overhead for encoding. However, because errors inevitably accumulate, there is a limit to computation size. Fault-tolerant quantum computers (FTQCs) carry out computation on encoded qubits, so they have overhead for the encoding and require quantum computers of at least a certain size. The gap between NISQ computers and FTQCs due to the amount of overhead is shown in Fig. 1. Is this gap unavoidable? Decades ago, many researchers would consider the answer to be in the negative. However, our team has recently demonstrated a new, unprecedented method to overcome this gap. Motivation to overcome this gap has also led to a research trend that started at around the same time worldwide. These efforts, collectively called early fault-tolerant quantum computing “early-FTQC”, have become a worldwide research movement. In this article, I introduce efficiency-improvement methods and novel efforts for early-FTQC.
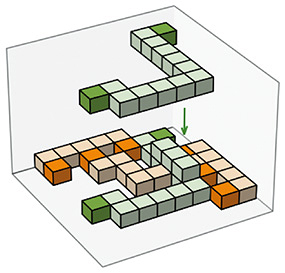
2. Possibilities and limitations of NISQ computersIn the article “Design and Development of Superconducting-quantum-computer System” [1] in this issue, a superconducting quantum computer that is currently operated as a cloud service in Japan is introduced. What is the extent of computation possible with a quantum computer of this scale? This quantum computer’s processor chip has 64 qubits. Under ideal conditions, it is considered to be capable of performing computations that cannot be done with current large-scale classical computers. In fact, Google published a paper in 2019 demonstrating a computation task using a processor with 53 qubits and the resulting quantum statistical effects, which would be difficult to classically simulate [2]. However, it is difficult to say that this computation task is useful. After the publication of the paper, several works were published arguing that even with classical computers, faster computation than expected is possible. Variational quantum eigensolver, a heuristic method for quantum computing that focuses on the efficient computation in the NISQ era has the potential to produce fast and useful computation by exploiting the characteristics of the quantum state, which classical computers do not have. However, there are issues that must be addressed. Because the variational quantum eigensolver is a heuristic method, it is not easy to show the theoretical proof of high-speed and high-precision computation. Realistic noise and error problems also occur when conditions are not ideal. Current quantum computers typically have an error rate of about 0.1 to 1% for a single gate operation. Roughly speaking, the total error rate increases with the number of gates, so 1000 gate operations would be difficult to achieve without error countermeasures. As introduced in the article “Quantum Error Mitigation and Its Progress” [3] in this issue, quantum error mitigation (QEM) is a class of techniques used to handle errors in the NISQ era. In the noisy computation described above, computational results are buried in errors. With QEM, the correct computational result is extrapolated by executing quantum computations several times to obtain multiple results and statistically estimating the errors. However, the greater the number of errors, the more difficult estimation becomes, and the greater the cost of repeatedly executing computations and performing measurements. In fact, the estimation becomes exponentially more difficult with the increase in errors, so there is a limit to the scale of computation for which QEM is practical. However, in June 2023, IBM published a paper discussing the use of a 127-qubit superconducting quantum computer to solve a condensed matter-physics problem that is difficult to handle with classical computation by ingeniously deploying QEM [4]. This achievement shows that the possibility of executing useful quantum computation that surpasses the capabilities of classical computation in the NISQ era continues to be pursued. Discussion is still ongoing about whether classical computation can handle such problems faster. 3. Improving FTQC efficiencyIs it the case, then, that quantum computers cannot overcome noise and errors and scale up further? It is known that error-correcting codes can also be applied to quantum computers. A fault-tolerant quantum computer (FTQC) can execute quantum computation on encoded qubits. An FTQC requires overhead, and the number of qubits needed is considered to be 1000 to 10,000 times that without encoding. As research and development of FTQC-architecture-based efficient encoding and decoding systems and compilers have just begun, improvement in efficiency is highly expected. We carried out several research projects to date on such improvements, and two are introduced as follows. The first project is on improving the efficiency of the computational process on encoded data. The standard method of quantum error correction is encoding with what are called surface codes. These codes work relatively efficiently with nearest-neighbor interactions between qubits arranged in a two-dimensional lattice and have a high fault-tolerant threshold. A promising method for executing quantum computation with surface code is lattice surgery. As shown in Fig. 2, we have shown that improving the efficiency of lattice surgery can be treated as a scheduling problem of computational paths in three dimensions, which takes into account the time axis of the computation, and have achieved several promising improvements in efficiency [5].
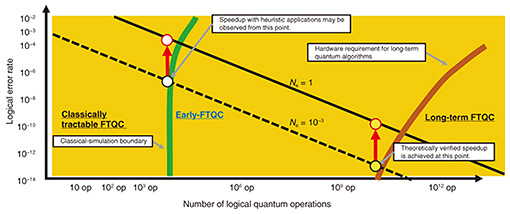
The second project is on improving the circuit efficiency of quantum algorithms. The task for determining the eigenenergy of the Hamiltonian in quantum chemistry and condensed matter physics by quantum phase estimation, a key quantum algorithm, is a representative approach of FTQC, showing quantum supremacy in practical problems. Compared with previous methods, qubitization [6, 7] converts the Hamiltonian into a form for which quantum-phase estimation is executable with fewer resources. To execute quantum-advantageous computation in the early-FTQC era, it is necessary to optimize the circuit elements in this qubitization. We reduced the number of T-gate operations, which incur computational costs in FTQCs. Specifically, we succeeded in reducing the number of T-gates in a quadratic polynomial manner for circuits for the Schwinger model [8]. 4. Early-FTQCIn the previous section, FTQCs and efforts to improve their efficiency were introduced. There are limits to improving the computation efficiency of an FTQC, and some overhead is inevitable. What costs are then incurred to run a useful FTQC? Figure 3 illustrates the FTQC regime. The horizontal axis represents the number of logical operations executed on the encoded quantum state. A logical operation including the overhead of computing on the encoded data is counted as one operation. The vertical axis represents the error rate of logical operations, i.e., the probability that an error will occur for each logical operation, which cannot be corrected despite using quantum error correction. The greater the number of logical operations and lower the logical error rate, the greater the scale of an FTQC can be run. The region to the left of the green line in this figure indicates the region where the scale of computation is tractable enough for classical simulation. The green line is curved at the top because a higher error rate makes it even easier to carry out classical simulation. The region to the right of the brown line represents long-term FTQCs. In this region, we can run algorithms in which the quantum advantage can be demonstrated for meaningful applications. The region between the green and brown lines is what we call early-FTQC [9]. This is the region from the boundary satisfying logical quantum supremacy to the boundary of long-term FTQCs. We believe that heuristic quantum algorithms exist in this region, and it is the region where an FTQC will be first run. Quantum algorithms used in the early-FTQC regime share many traits with NISQ algorithms. The major difference from NISQ era is that because early-FTQC have acquired fault tolerance, they will continue to execute larger computations as quantum computers are scaled up. In other words, as the size of the quantum computer increases, the potential for better computation increases.
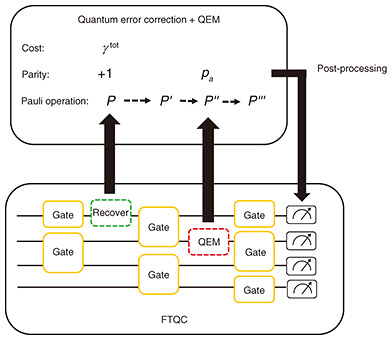
Are there ways to further hasten the achievement of early-FTQC? The efficiency-improvement methods described in the previous section are of course significant and effective. Another proposal is rewriting the circuit for algorithms to reduce the number of qubits by incorporating the classical post-processing procedure [10]. Our team has also presented a novel method of applying QEM, considered to be a class of techniques for the NISQ era, to hasten the achievement of early-FTQC [9]. This method adapts a quasi-probability method, a QEM technique mentioned above, to an FTQC. Unlike quasi-probability methods for the NISQ era, we do not mitigate physical errors but logical errors. As shown in Fig. 4, recovery operations for error correction in an FTQC are carried out using fundamental quantum operations called Pauli operations. Because Pauli operations are simple, they can be efficiently carried out in batches as the final classical post-processing procedure. In many cases, quasi-probability-based QEM can also be carried out using Pauli operations, so it can be incorporated into the classical post-processing procedure. In some cases, it cannot be carried out with Pauli operations. In this case, the process is carried out physically (see [9] for details).
What becomes important is the cost of QEM. Because the variance of results increases as the amount of errors increases, we need the cost of repeating computations to statistically estimate errors and obtain the correct result. Because there is no error-correction function in NISQ computers, the amount of errors increases as the quantum-computation size increases. Because QEM cost increases exponentially, there is a practical limit to the computation size for which QEM can be used. An FTQC is equipped with error correction, so a region where QEM can be used within reasonable parameters always exists when computation size increases. In an FTQC, the code distance and overhead are normally set so that the number of errors remaining in the computation results to obtain the correct result is sufficiently smaller than 1 (the line Ne = 10−3 in Fig. 3). If QEM is applied to an FTQC, the number of errors can be relaxed to about 1 (the line Ne = 1 in Fig. 3), code distance can be shortened, and overhead needed for error correction can be reduced. As indicated with the red arrows in Fig. 3, the region of early-FTQC is expanded (the region of long-term FTQC is also similarly expanded.) In fact, we have shown that by using QEM, the number of qubits required for an FTQC can be reduced by about 80%. In other words, using the same number of qubits, quantum computation size can be increased 1000-fold in terms of the number of quantum operations due to the effect of QEM. 5. Further development of early-FTQCEarly-FTQC has been progressing with various implications. Early-FTQC in a broader sense has also been investigated so far. Early-FTQC described in the previous section meant the initial stages of an FTQC and efforts to hasten the achievement of FTQCs. However, the concept of early-FTQC as a “partial” FTQC, occupying the intermediate stage between a NISQ computing and full-fledged FTQC, has recently emerged. For example, a partial FTQC architecture was proposed in which circuit elements called Clifford gates, which have small encoding overhead, are error corrected, while the rotating gate circuit elements, which are known to incur large overhead for error correction in quantum computation, are not error corrected [11]. In this case, errors accumulate in the rotation gates, so quantum-computation size is limited by this characteristic. However, compared with NISQ computers, this architecture is believed to enable larger quantum computation. We have also proposed a virtual quantum-error-detection protocol that seeks an intermediate procedure between QEM and quantum error correction [12]. Research and development such as that to bridge the gap between NISQ computers and FTQCs have begun. If it becomes possible to freely choose the appropriate error-correction capability and connect a NISQ computer and FTQC, it will be possible to continue to develop quantum computers that perform better than before as computation size increases without incurring gaps from encoding overheads. This new era may soon be a reality. References
|
|||||||||||||||||||||||||