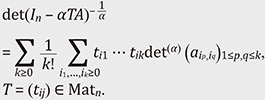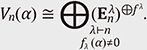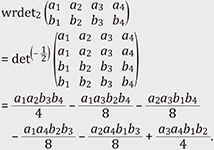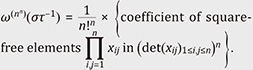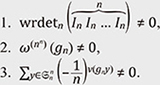|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Feature Articles: Challenging the Unknown: Mathematical Research and Its Dreams Vol. 22, No. 9, pp. 45–52, Sept. 2024. https://doi.org/10.53829/ntr202409fa5 Representation Theory and Combinatorics Arising from DeterminantsAbstractOriginating from the unified treatment of probability distributions, the α-determinant is a one-parameter interpolation of the determinant and permanent of a matrix. While it generally does not have the invariance properties of the determinant, the irreducible representations of the associated general linear (Lie) groups define interesting invariants that unveil a new and rich mathematical theory with abundant unsolved problems, related to symmetric functions, representation theory, combinatorics, number theory, probability and other areas. Keywords: ¦Á-determinant, wreath determinant, irreducible decomposition of representations 1. IntroductionIn this article, we focus on matrix Lie groups, that is, groups of matrices with the operation of the usual matrix product (i.e., composition of linear forms), the most basic example of which is the general linear group over the complex numbers. Since Lie groups are also geometrical objects (differentiable manifolds), both the group structure and differentiable structure coexist in a single object and must be accounted for. Starting from certain special representations of these groups, we introduce research on several areas of mathematics, including new research directions and open problems. 1.1 GroupsA group G is a set with an operation (generically called “product”) G × G ∋ (g, h) → gh ∈ G that is associative, i.e., (gh)k = g(hk) for g, h, k ∈ G. In addition, G must have an identity element e ∈ G such that ge = eg = g holds for all g ∈ G, and for all g ∈ G there must be an inverse element g–1 such that gg–1 = g–1 g = e. The main examples of groups in this article are the symmetric group of m elements 𝔖m, i.e., the groups of permutations of m letters with the operation of composition, and the general linear group GLn(ℝ) (resp. GLn(ℂ)), the group of n dimensional square nonsingular (invertible) matrices with real (resp. complex) entries with the usual matrix multiplication. 1.2 Lie groups, Lie Algebras and their representationsA representation (𝜋, V) of G is a group homomorphism 𝜋 from G to the group of linear transformations GL(V) of a vector space V. We normally consider only vector spaces over the complex numbers. In this setting, we say that G acts on V, or that V is a G-module, and if it is clear from the context, we omit the notation 𝜋. To consider an infinite dimensional V, it is indispensable to introduce the notion of topology; thus, we only consider finite dimension. By introducing a Hermitian inner product to the n-dimensional V, we may consider the group U(n) of unitary matrices, the group of matrices that leave the inner product invariant. The development of representation theory took place in parallel with the revolutionary physical theories of relativity and quantum physics, resulting in a notation and terminology that mixes mathematical and physical subtleties and may be confusing at first but that is not without merit. As mentioned above, Lie groups are manifolds with geometric structure and notions such as “curvature” and “connectedness,” so they cannot be described faithfully only with linear algebra. Because of this, and to the extent possible, instead of G, we consider the associated “differentiated” Lie algebra 𝔤. Since 𝔤 is equivalent as a vector space to the set of tangent vectors at the identity e ∈ G, its action is regarded as the infinitesimal version of the Lie group action. In this article, we only consider finite-dimensional representations, so Lie algebras suffice, but we note that this is not the case for general Lie groups and representations. The Lie algebra 𝔤𝔩n(ℂ) of the Lie group GLn(ℂ) is the ring of all n-dimensional matrices. For a matrix X ∈ 𝔤𝔩n(ℂ), the exponential map satisfies det(expX) = etrX ≠ 0, thus expX ∈ GLn(ℂ) is the corresponding Lie group element. Therefore, if the action of GLn(ℂ) on a polynomial ƒ over Matn is (g. ƒ)(x) = ƒ(g–1x), the infinitesimal action of 𝔤𝔩n(ℂ) is given by
1.3 Motivation for the representation theoretical study of α-determinantThe α-determinant is a generalization of both the determinant and permanent*. In the definition of the α-determinant, given below, the sign changes appearing in the definition of the determinant are replaced with certain weights depending on the parameter α. By setting α = –1 we recover the definition of the usual determinant and with α = 1, that of the permanent. It was originally introduced as α-permanent by Vere-Jones [1] in the context of probability theory. The name α-determinant follows the convention of Tomoyuki Shirai and Yoichiro Takahashi [2]. They used the α-determinant to construct point processes that generalize the ones used in finance and time-series analysis, namely, the boson point process, fermion point process, and Poisson point process. Surprisingly, when α ≠ –1 the α-determinant loses the multiplicative property of the usual determinant, that is, det(AB) = det(A) det(B). Thus, we immediately ask the following problem question. Problem 1: Where did the multiplicative property go? The determinant is a one-dimensional representation of GLn (ℂ). While the permanent does not define a one-dimensional representation, it defines an irreducible representation of the vector space spanned by the symmetric tensor product. With irreducible representation, we refer to a subspace of V, different from {0} and V itself, that is invariant under the action of G. Informally, we may think of irreducible representations as prime numbers or elementary particles in particle physics. Therefore, we may also ask the following problem question. Problem 2: For general α, what is the structure of the spaces spanned as the group acts on the α-determinant? These two questions sparked the interest of the second author of this article in the representation theory of the α-determinant [3].
2. The α-determinantFor a fixed α, the α-determinant of a square matrix A = (aij) ∈ Matn is a modification of the usual determinant defined as
Here, νn(σ) is the cycle number of a permutation σ ∈ 𝔖n, i.e., the number of cycles in the cycle decomposition of σ. Hereafter, we write ν(σ) := n – νn(σ) and note that ν(σ) is the minimum number of transpositions required to express σ. A theorem of Vere-Jones [1] is that
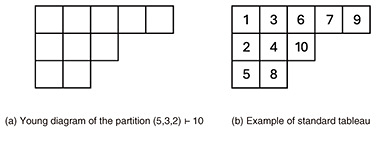
We refer the reader to a previous study [4] for details on the discovery of the formula and its applications. 2.1 Preliminaries from representation theoryIt is well known that the finite dimensional irreducible representations (irreducible 𝔤𝔩n-modules) of GLn(ℂ) and its Lie algebra 𝔤𝔩n(ℂ) are parametrized by the so-called highest weights. With respect to the standard action of GLn(ℂ) on ℂn, the natural action of GLn(ℂ) on the tensor product (ℂn)⊗m commutes with the action of 𝔖𝔪 permuting the m spaces in the tensor product, because there is a duality between the two actions. This is the well-known Schur–Weyl duality [5]. From this perspective, the highest weights are identified with partitions of integers. We say that the vector of non-negative integers λ = (λ1, λ2, …, ..) is a partition of n, written as λ ⊢ n, when it satisfies n = λ1 + λ2, + ¡Ä (λ1 ≥ λ2 ≥ …). The length l(λ) is the number non-zero parts of the partition λ. A λ is often identified with the associated Young diagram, defined by {(i, j) ∈ ℤ2¨¢1 ≤ j ≤ λi, i ≥ 1}. It is customary to illustrate the Young diagrams as left-aligned arrangements of boxes with λi boxes in the i-th row, as shown in Fig. 1(a). If we arrange the n numbers 1, 2, …, n in a Young diagram λ such that numbers in a row increase from left to right and in each column the numbers increase from top to bottom we obtain a standard tableau of shape λ (Fig. 1(b)). The set Stab(λ) is the set of all standard tableaus of shape λ and is a fundamental notion in the representation theory of the symmetric group.
2.2 Cyclic modules arising from α-determinantThe action of 𝔤𝔩n(ℂ) on the ring of polynomial functions 𝒜(Matn) on the variables {xij}1≤i,j≤n is given by the differential operators
Here, {Eij} (1 ≤ i, j ≤ n) is the standard (matrix elements) basis of 𝔤𝔩n(ℂ). For X = (xij), we denote as Vn(α) the cyclic 𝔤𝔩n(ℂ)-module generated by det(α)X. In other words, Vn(α) is the vector space (module) generated by the (repeated) action of elements of 𝔤𝔩n(ℂ) on det(α)X ∈ 𝒜(Matn). For α = –1, we have det(α)X = detX; thus, Vn(–1) = ℂ⋅detX. Therefore, the study of the structure of Vn(α) is an important step towards the answer to both Problems 1 and 2. Theorem 2.1 [3]. Let
Here, ƒλ := |Stab(λ)| and ƒλ(x) := ∏(i,j)∈λ (1 + (j – i)x) is the content polynomial of λ. This theorem shows that if α ∉ It is also natural to generalize this situation and consider the cyclic 𝔤𝔩n-module generated by the power (det(α)X)l. In this case, the highest weight modules appearing in the decomposition have nontrivial multiplicity given by a combinatorial quantity, and computing this multiplicity is generally a difficult problem. When n = 2, the pair (𝔖2l, 𝔖l × 𝔖l ) of a symmetric group and Young subgroup is a Gelfand pair, which enables one to write the multiplicity in terms of zonal spherical functions given explicitly by hypergeometric polynomials [6]. The general case is still open and currently there is not even a conjectural form for the multiplicity. Moreover, one of the classic and fundamental notions in the theory of symmetric functions is plethysms [7]. In a previous study [8], for the power of det(1)(X) (permanent) and the generated cyclic module structure, a conjecture that is related with plethysms for the symmetric tensor product was presented. The case of general n appears to be difficult, but it has been verified for n = 2 and arbitrary l, as well as for n = 3 and l = 2. Note that analogous research has been conducted for quantum groups [9]. For n = 2, the multiplicity is given both by hypergeometric polynomials and q-hypergeometric polynomials. This is a fascinating and promising line of research [10, 11]. 3. Wreath determinantAs discussed in the previous section, when α takes the values ± Let K denote the subgroup of 𝔖n consisting of permutations that fix any elements except from k + 1 taken (arbitrary) from 1, 2, …, n. Then, for A ∈ Matn we observe that the sum ∑σ∈K det(α) (AP(σ)) contains the factor (1 + α)(1 + 2α) … (1 + kα) (A ∈ Matn), where P(σ) is the permutation matrix of σ ∈ 𝔖p. In other words, the sum ∑σ∈K det(– Since det(α) (AP(σ)) = det(α) (P(σ)A), the foregoing discussion holds similarly for rows. A consequence of the weak alternating property is that we have analogs of Vandermonde and Cauchy determinant formulas [12]. 3.1 Invariant theory of wreath determinantsWe denote by 1p,q the matrix of size p × q with all entries equal to 1. For A ∈ Matn,kn, the k-wreath determinant is defined by
For example, we have
Like the usual determinant, the wreath determinant is characterized by its left-GLk, right-𝔖k ≀ 𝔖n relative invariance. Here, 𝔖k ≀ 𝔖n is the wreath product of the groups 𝔖k and 𝔖n and is defined using the concept of the semidirect product of groups (a technique used to obtain a new group from two known groups). Theorem 3.1 [12]. A map ƒ: Matn,kn → ℂ with properties 1. ƒ is a multilinear map with respect to the columns, 2. ƒ(QA) = (detQ)k ƒ(A) holds for any Q ∈ Matn, that is, ƒ is left-GLk relative invariant, and 3. ƒ(AP(σ)) = ±ƒ(A) holds for any σ ∈ 𝔖k ≀ 𝔖n (if σ ∈ is equal to the map A ↦ wrdetk A up to a scalar multiple. While this theorem may be proved in an elementary manner, it is also an easy consequence of the invariant theory of the underlying (GLn, GLkn)-duality. 3.2 An analog of group determinant for group-subgroup pairs using wreath determinantsFerdinand Georg Frobenius developed the theory of group characters in his study of the group determinant for non-abelian groups. For a finite G, consider an indeterminate xg for each group element g ∈ G, then the group determinant is given by
The group determinant is a complete invariant with respect to the isomorphism classes of groups. Concretely, it holds that Θ(G) = Θ(G') ⇔ G ≅ G'. The main result of Frobenius is the factorization of the group determinant into irreducible polynomials with coefficients given by the group characters, in modern terms this is equivalent to the decomposition of the regular representation of a group (the action of G on its group ring) into irreducible representations. The origin of the work of Frobenius in the group determinant is a letter by Richard Dedekind in 1896. Dedekind had previously discovered how to factorize the group determinant for abelian groups and posed the problem for general non-abelian finite groups to Frobenius. It is not an exaggeration to say that this letter marked the beginning of representation theory of finite groups. Recall that the k-wreath determinant is defined for n × kn matrices; therefore, by considering a pair (G, H) of a finite G and subgroup H of index k, by analogy we may define
Note that since the wreath determinant does not have an invariance with respect to column transpositions, this definition depends on the ordering of the matrix columns and rows. Therefore, it is necessary to consider a fixed numbering (or naming) of the group elements. For a fixed bijection ϕ: {0, 1, …, kn – 1} → G, we say that gi = ϕ(i) is a numbering of G. For a ℂ-algebra A (e.g. a polynomial ring in kn – 1 variables) a map ƒ: gi ↦ qi is called specialization. When G is an abelian group, for a reasonable numbering of the elements of G, we may consider the specialization ƒ: gi ↦ qi to see that the determinant Θ(G, H) factors into products of polynomials of the form qi – 1 [13]. Let us give a concrete example. From the partition (k, …, k) ⊢ kn and corresponding irreducible characters χ(kn) of
Example 3.2. For G = ℤn × ℤn and H = ℤn × {0}, we have
Here, σ, τ ∈
Note that if n = 3, we have Θ(G, H) = 0. A comprehensive theory of group-subgroup wreath determinant has not yet been developed, but two related developments have surfaced, one is related to the Alon–Tarsi conjecture by Kazufumi Kimoto and the other is the construction of new graphs based on group and subgroups. 3.3 Alon–Tarsi conjectureA Latin square is a square arrangement (i.e. a n × n matrix) filled with the numbers 1 ∼ n in such a way that in each row and column, each number appears exactly once. For instance, the 12 Latin squares of size 3 are
The sign sgn L of a Latin square L is the product of the signs of all column and row permutations. If sgn L = 1, we say L is even and odd if sgn L = –1. If n is an odd number, the formula sgn(P((1,2))L) = (–1)n sgn L holds for the transposition (1,2), giving a bijection between odd and even Latin squares and showing that the number of odd and even Latin squares of odd size n is equal. For even numbers the problem is still open. Conjecture 3.3 (Alon–Tarsi conjecture 1992). For an even number n, the number of even and odd Latin squares of size n is different. While the conjecture originated in graph coloring problems, it has interesting and nontrivial equivalent formulations such as the Rota basis conjecture on a certain special choice of basis for an n dimensional vector spaces, and the non-vanishing of certain integrals over the special unitary group SU(n) with respect to the square-free coordinate product Haar measure (SU(n) bi-invariant measure). Kimoto also discovered the equivalence of the Alon–Tarsi conjecture in terms of the wreath determinant [12]. Theorem 3.4. Let n be an even number. The Alon–Tarsi conjecture is equivalent to any of the following three statements below.
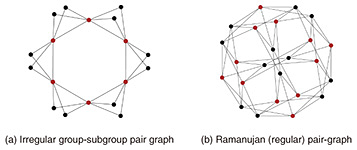
Here, gn ∈ The Alon–Tarsi conjecture is easy to verify for specific cases, but as usual in number theory and combinatorics, the proof appears to be a formidable challenge. The best results to date are those of Drisko (1997) for n = p + 1, where p is a prime number, and of Glynn (2010) for n = p – 1 (see [14] for a review up to 2019). It is worth mentioning that an alternative proof of the latter result using the wreath determinant has been given by Kimoto [15, 16]. For the number of Latin squares ls(n), although it is a weak result, we remark that the asymptotic formula ls(n)1/n2) ∼ e–2n is known [17]. One of the reasons that explains that the Alon–Tarsi conjecture may be difficult to solve is that the number of even and odd Latin squares appear to be asymptotically equal. Let us propose a new research problem. Problem 3.5. Find a suitable definition of a Latin square zeta function ζLS (s) such that we have the following equivalence: best estimate in the prime number theorem (↔ Riemann hypothesis): ζ(s) = Alon–Tarsi conjecture ζLS(s). In other words, such that the Alon–Tarsi conjecture is equivalent to a Riemann hypothesis’ analog for ζLS(s), it might be helpful to compare the Alon–Tarsi conjecture with the phenomenon of Chebyshev’s bias for prime numbers. 3.4 Group-subgroup pair graphsIn graph theory, there is an important class of graphs known as Ramanujan graphs. Ramanujan graphs are theoretically the best expanders, i.e., graphs with rapid mixing and good diffusion properties. The properties of Ramanujan graphs make them particularly important for applications, including the construction of cryptographic hash functions. A graph being Ramanujan is equivalent to the analog of Riemann Hypothesis for the Ihara zeta function of the graph, making it also interesting from the point of view of number theory. The main problem in this area is the construction of explicit families of Ramanujan graphs of fixed degree. Some known examples are the Lubotzky–Phillips–Sarnak graphs (1994), constructed with Cayley graphs of projective linear groups over finite fields using the theory of Hamiltonian quaternion algebras and their maximal orders, and Pizer graphs (1990), based on the theory of isomorphism classes (isogenies) of hyperelliptic curves over finite fields. In the former, for a prime number p congruent to 1 modulo 4, the resulting graphs are a family of (p + 1)-regular Ramanujan graphs. A Cayley graph is a regular graph constructed from the elements of a finitely generated G and where the edges are defined using the (group) multiplication using a generating set S. A new research direction is defining hash functions for group-subgroup pair graphs, which are a generalization of Cayley graphs (see Fig. 2), and studying their cryptographic properties [18]. For a G, subgroup H and a subset S ⊂ G such that S ∩ H is a symmetric set, the group-subgroup pair graph, or simply pair-graph, 𝒢(G, H, S) is a graph defined in a manner analogous to Cayley graphs, but such that the resulting graph is not generally regular. Concretely, 𝒢(G, H, S) is a graph, the vertices of which are the elements of G and such that h ∈ H and g ∈ G are connected by an edge when they satisfy the relation h ∼ g ⇔ g = hs (s ∈ S) [19]. While examples of Ramanujan group-subgroup pair graphs are known for the regular case (see Fig. 2(b)), infinite families have not yet been constructed. The construction of infinite families of Ramanujan graphs is one of the major goals in the theory of pair-graphs from the point of both mathematics and applications.
4. Perspectives on positive singular values: Wishart distribution, Wallace sets, and positivity of α-determinantA natural problem is to consider the positive case α = The study of positive definite functions on convex cones on Euclidean spaces has applications to several areas, including optimization and probability. In the analysis of Hilbert spaces of holomorphic functions on symmetric cones (symmetric spaces of Lie groups) and its unitary representation, there is an important notion called Wallach set. For the integral kernel of symmetric cones, the set is basically given by reciprocals α = In statistics, there is multivariate generalization of the χ-square distribution for positive definite matrices, called Wishart distribution. Let n mutually independent p-variate random vectors {x1, x2, …, xn}, with n ≥ p, follow a multivariate normal distribution N(0, Σ) with mean 0 and covariance matrix Σ. Then, the random variable References
|
|||||||||||||||||||||||||||||||||||||||||||||