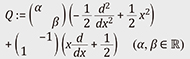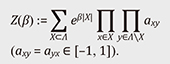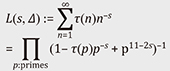|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Feature Articles: Challenging the Unknown: Mathematical Research and Its Dreams Vol. 22, No. 9, pp. 65–72, Sept. 2024. https://doi.org/10.53829/ntr202409fa8 Light-matter Interaction and Zeta FunctionsAbstractKnowledge of the partition and spectral zeta function of a quantum system is fundamental for both physics and mathematics, and the positions these functions occupy in their respective fields share a common philosophy. In this article, we describe the number theoretic structures hidden behind light and matter interaction models, focusing on the partition function and special values of the spectral zeta function, highlighting how modern mathematical research is involved. Keywords: quantum Rabi model, non-commutative harmonic oscillator, partition function 1. IntroductionThe historical origin of mathematics was the process of counting. Two fundamental results of early mathematics, believed to be discovered at the Pythagorean school and documented by Euclid around 2500 years ago, are 1) the number of prime numbers is infinite, and 2) any natural number can be uniquely factorized into prime factors. One of the most fascinating aspects of number theory is the stark contrast between the simplicity of the integers and the complex and seemingly irregular distribution of prime numbers. The distribution of prime numbers is still a subject of research and takes a concrete form in the Riemann hypothesis, the most well-known open problem in mathematics, still unsolved after 165 years. In the modern world, the development of quantum information technologies requires the understanding and control of light and matter interactions. The most fundamental theoretical model of this type of quantum interaction is the quantum Rabi model (QRM) [1]. In applications, the systems are always subject to the passing of time, so it is fundamental to understand the time evolution of the system, mathematically controlled by the partition function and heat kernel of the system. Informally speaking, the essence of the partition function is to allow the discernment of properties of ensembles of particles (macro level) having independent states (micro level). More concretely, the partition function is defined as the sum of certain weighted values depending on all the possible states of the system. Similarly, the Riemann zeta function is also defined as the product of geometric series defined for all prime numbers, each prime number existing independently from the others. The Riemann zeta function enables us to perfectly understand the distribution of the prime numbers, impossible only looking at the individual prime numbers, in the Riemann hypothesis. Surprisingly, physics and number theory share a similar philosophy, and the connections do not end here. For instance, the partition function of the quantum harmonic oscillator and Riemann zeta function are explicitly connected. It is generally equivalent to consider the partition function and the spectral zeta function (the Dirichlet series associated with the eigenvalues) of a quantized physical system. The mathematical theory that bridges the two worlds is representation theory, historically developed alongside relativity theory and quantum mechanics. In this article, we give an overview of the theory of the partition function and spectral zeta function of quantum interaction models with the hope that the reader will discover and appreciate the bonds between quantum physics and number theory. Hereafter, we denote the ring of integers, field of rational numbers, field of real numbers, and field of complex numbers as ℤ, ℚ, ℝ, and ℂ, respectively. 2. Special values of the Riemann zeta function and automorphic formsThe harmonic series, the sum of the reciprocals of all positive integers, was known to diverge since the Middle Ages, with an ingenious proof by Nicole Oresme in the 14th century. What about the sum of the reciprocal of the squares? This question, later known as the Basel*1 problem, was posed by the Bolognese mathematician Pietro Mengoli in 1644. The problem remained unsolved for almost 90 years, until Leonhard Euler discovered in 1735 that it converges to the exact value These results on the harmonic series may be written as ζ(1) = +∞, and ζ(2) =
The middle equality connecting the series and the Euler product manifest the fact that any integer can be factored uniquely into prime factors. The domain of absolute convergence of the series and the infinite product is the half-plane ℜ(s) > 1, and it is known that the Riemann zeta ζ(s) can be extended analytically into a meromorphic function defined in the whole complex plane with a unique simple pole*2 at s = 1. Euler solved the Basel problem by comparing infinite product expansion of sin(𝜋x) with the Taylor series of second order and discovered that the values of the zeta function ζ(2n) at the even integers are given by
where Bn are the Bernoulli numbers defined by the generating series In contrast, the passing of time has not illuminated the question of irrationality (or rationality) of the special values at odd integers. The first nontrivial odd value, ζ(3), had to wait until 1979 to be shown to be irrational by Apéry [2]. Apéry defined mysterious sequences of numbers, now called Apéry numbers, and used them in an inventive way to prove that ζ(2) and ζ(3) are irrational numbers. Even today, not much else is known about the properties of the remaining odd special values. At the turn of the 21st century, Rivoal proved that the sequence ζ(2n + 1)(n = 2, 3, …) contains infinite number of irrational numbers, and that there is at least one irrational among the numbers ζ(5), ζ(7), ζ(9), …, ζ(21). Shortly after, in 2001 Zudilin improved the result to show that the numbers ζ(5), ζ(7), ζ(9), ζ(11) contain at least one irrational. This is the present state of knowledge about this question, at least here on planet Earth. 2.1 The prime number theoremThe prime number theorem, a result describing the distribution of prime numbers, was conjectured by Carl Friedrich Gauss and Adrien-Marie Legendre in the 18th century and proved independently by Charles de la Vallé Poussin and Jacques Hadamard in 1896 using the ideas introduced by Bernhard Riemann in his seminal work in number theory. If 𝜋(x) is the function describing the number of primes less than x(> 0), then the prime number theorem is precisely stated as
Here, ƒ(x)∼g(x) means that the limit ƒ(x)/g(x) → 1 holds as x → ∞. At the heart of the proof is Riemann’s idea that ζ(s) ≠ 0 for ℜ(s) = 1. The revolutionary contribution of Riemann of recognizing that the seemingly random distribution of prime numbers is intimately related to the analytical properties of ζ(s) may even be a greater achievement that a future proof of the Riemann hypothesis itself. 2.2 Functional equation of the Riemann zeta functionOne of the main features of ζ(s) is the functional equation. Let Γ(s) be the gamma function, and set ζ̃(s) := 𝜋–s/2Γ(s/2)ζ(s), then the functional equation is ζ̃(1 – s) = ζ̃(s). The essential idea of the functional equation was discovered by Euler in its computations aimed to assign values to divergent series, including
The computational results obtained by Euler are correct even though the concept of analytical continuation (or even complex function theory) did not exist at the time. Let us give an outline of the proof of the functional equation to introduce some of the ideas used later for the partition function. To avoid technical complications, we assume that all series and integrals converge and behave in a reasonable manner. The Mellin transform ℳƒ of a function ƒ is defined by
A fundamental example is given by ƒ(t) = e–nt with t > 0 with Mellin transform ℳƒ(s) = n–sΓ(s), verified directly from the definition of Γ(s). Similarly, for a series Let us define the series θ(z) in the upper-half complex plane ℍ := {z ∈ ℂ 𝔍(s) > 0} as
From the foregoing discussion, we verify that by setting Automorphic functions (resp. forms) are functions that are invariant (resp. almost invariant) under certain actions of non-commutative groups. Trigonometric functions are well-known to be invariant under translations (i.e. are periodic functions), in other words, they are invariant under the action of the abelian group ℤ. Thus, in this sense automorphic functions may be thought as non-commutative versions of trigonometric functions. For z ∈ ℍ, in addition to the translation invariance θ(z + 2) = θ(z), the theta function satisfies the relation
and replacing by the rapidly decreasing function ƒt(x) = e–𝜋tx2, we obtain the desired relation. Finally, for z = it (t > 0), we obtain Let us give an interpretation of the Poisson summation used above. Similar to the idea of the hands on a clock*3, we consider two real numbers to be equivalent if they have the same fractional part and write this set as ℤ∖ℝ. With this in mind, the right side of the Poisson summation formula is the sum over the lengths of a circumference (i.e., number of turns), and the left side is the sum over the irreducible representations that appear in the Fourier transform, that is, representations x ↦ e2𝜋iyx of the abelian group ℝ that are trivial on ℤ. In other words, we might think of it as a sum over all y = m ∈ ℤ. The left side may also be interpreted as the sum over the eigenvalues of the Laplacian Δ = – 2.3 Modular and automorphic formsLet SL2(ℤ) (respectively SL2(ℝ)), be the group of 2 × 2 matrices with integer (respectively real) entries and determinant 1. The group SL2(ℤ) is generated*5 by matrices
Now, This is the type of stage where automorphic forms (modular forms) reside. Note that in this case we do not make a distinction between ±1. The theta function θ(z) above, is almost invariant under the action of the subgroup Γ(2) (≅ Γ0(4)) of SL2(ℤ) generated by S and T2, and is therefore called a Γ(2)-automorphic form.
3. Quantum interaction models3.1 QRMIn quantum optics, the QRM is the most fundamental model to describe light-matter interaction. Its Hamiltonian is given by HRabi := a†a + Δσz + gσx(a† + a). Here,
are the Pauli matrices for a two-level system (particle, qubit or “matter”), g > 0 is the coupling strength between the two-level system and the photon, and 2Δ > 0 is the energy difference between the levels of the two-level system. We may assume that the Hamiltonian HRabi acts on the Hilbert space L2(ℝ) ⊗ ℂ2 of integrable two-dimensional vector-valued functions. The addition of a bias term to the Hamiltonian HRabi results in the model 3.2 Non-commutative harmonic oscillatorThe non-commutative harmonic oscillator (NCHO) [4, 5] is defined as a system of ordinary differential equations having a Hamiltonian
acting on L2(ℝ) ⊗ ℂ2. When the parameters α, β > 0 satisfy αβ > 1, Q is a self-adjoint operator having only the discrete spectrum (0 <)λ0 ≤ λ1 ≤ ⋯ ≤ λn ≤ ⋯ ↑ ∞ with multiplicity of at most 2. The spectral zeta function ζQ(s) of the NCHO is given by
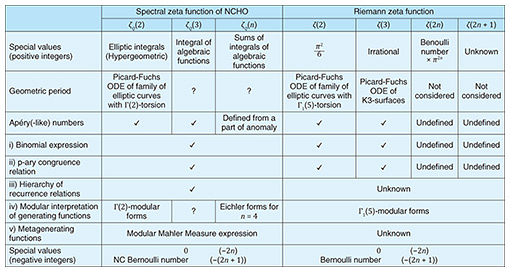
Note that when α = β, Q is unitarily equivalent to a couple of harmonic oscillators; thus, ζQ(s) = It is also possible to define analogs of the Apéry numbers from the special values ζQ(2), ζQ(3), ζQ(4) that unveil a rich mathematical structure. For instance, for ζQ(2), there are explicit relations with automorphic forms and elliptic curves (Table 1). For ζQ(4), one has to venture beyond the usual modular forms and consider natural extensions of Eichler forms (given by generalized Abel integrals) [7] associated with a new cohomology [8, 9]. In the explicit description of the Apéry-like numbers one also encounters integrals of generalized Eisenstein series [10], deeply related to the research started by Shimura in 1982 on holomorphic modular forms for one variable [11].
3.3 Covering modelsOne of the motivations for the introduction of the NCHO was to slightly weaken the symmetries imposed on the quantum harmonic oscillator to rise above the Gauss hypergeometric functions appearing in classic representation theory and to consider the resulting spectral zeta function as an extension of ζ(s). In practice, by using representation theory, we can see that the eigenvalue problem of the NCHO does goes beyond the Gaussian hypergeometric differential equations*6 and corresponds to the existence of holomorphic solutions of a Heun ordinary differential equation (ODE), with four singular points {0, 1, αβ, ∞}, in a region containing {0, 1} but not αβ [12, 13]. By joining the singular point αβ and ∞ via a confluence process, we obtain a confluent Heun ODE, which corresponds directly to the eigenvalue problem of the QRM. We may thus say that the NCHO is a covering model of the QRM by looking at the corresponding Heun ODE pictures [13]. The same covering relation holds for the η-NCHO, a shifted version of the NCHO and AQRM [14]. It was discovered [15] that the eigenvalue problem of the NCHO gives rise to a long-established physical model called the two-photon quantum Rabi model (tpQRM) [16]. This shows that the interaction between one photon and a two-level atom (QRM) can be obtained from that between two photons and a two-level atom (tpQRM) via the covering relation. It would be interesting to confirm the mathematical concept of covering between these physical models through actual experiments. It is also worth remarking that in a previous study [15], using representation theory, the covering relation takes a simpler and clearer form. Further exploring the physical and number theoretical implications of the covering relations is one of the promising research directions in this area. 3.4 Partition function and spectral zeta functionsIn this section, we consider a quantum system with self-adjoint Hamiltonian H. As mentioned in the introduction, we are interested in knowing the action of the unitary operator exp(–itH) (propagator/heat kernel) and its trace, the partition function ZH(β) of H. The partition function is defined as the sum of the Boltzmann factors exp(–βE(μ)), where E(μ) is the energy (eigenvalue) of the state μ, that is, it is given by
where Ω is the set of all possible eigenstates of H. The partition function is one of the fundamental tools of statistical mechanics for the study of entropy and other properties of a system in thermodynamical equilibrium. On the other hand, the spectral zeta function ζH(s) is defined as the Dirichlet series determined by the eigenvalue sequence E(μ). We assume for simplicity*7 that E(μ) ≠ 0. Concretely, ζH(s) is given by
Therefore, by the definition of Γ(s), the two functions are connected via the Mellin transform
It is important to mention that the long awaited explicit formulas of the heat kernel and partition function of the QRM and AQRM were finally obtained [17–19]. The technique for the computation is based on the Trotter–Kato product formula, regarded as the mathematical formulation of the Feynman path integral, multivariate Gaussian integrals and the Fourier transform in The partition function also provides a short proof of the analytic continuation of the corresponding spectral zeta function using a path integral expression going from infinity to the origin, then circling the origin and back to infinity*8, and extensions of Bernoulli numbers for the spectral zeta function (e.g. Rabi-Bernoulli polynomials for the QRM). Note that the partition function can be recovered from the Rabi-Bernoulli polynomials since the Laurent expansion at the origin of the generating functions of the Rabi-Bernoulli polynomials is equal to the partition function. Although integral expressions for the positive integer points for the spectral zeta function of the NCHO are known, an explicit expression for the partition function has not been obtained. The values at negative integers may also be regarded as a generalization of Bernoulli numbers, called NC-Bernoulli numbers. Therefore, we might expect that the partition function is given by the Laurent series at the origin of the generating function of the NC-Bernoulli numbers. Unfortunately, at present, even with strong supporting evidence, it remains as a conjecture [20]. Nevertheless, the research towards conjecture has illuminated several aspects of the theory. For instance, to work with the formal expressions of the special values of the spectral zeta functions arising from the partition functions, it is useful to consider Borel-summation and non-Archimedian methods to deal with certain divergent series. In particular, certain expressions of special values of zeta functions that are divergent in ℝ may be interpreted as special values of zeta (Hurwitz type) functions [21] defined in the p-adic fields ℚp [20].
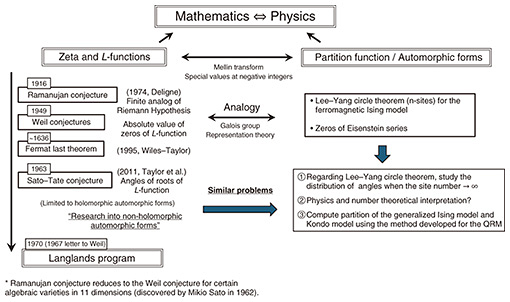
4. L-functions and the structure of zeros of partition functionTable 1 shows a comparison between the zeta functions ζQ(s) and ζ(s). As mentioned above, if we let α/β → 1 in ζQ(s), we essentially obtain ζ(s). However, what it is important is that ζQ(s) reveals a structure that is not visible in ζ(s). It is also worth remarking that we cannot expect ζQ(s) to have an Euler product expression or functional equation. In fact, the integral expressions at positive integer points obtained in a previous study [9] suggest that ζQ(s) may be expressed as a sum of number theoretical L-functions (zeta functions associated to certain representations). If this conjecture is correct, then even if the individual L-functions have functional equations, ζQ(s) may not have one. Similarly, the lack of a functional equation is not a contradiction since the axis of symmetry (the line On the right of Fig. 1, one of the points involves the partition function of the ferromagnetic Ising model, given by
In particular, the Lee–Yang circle theorem (1952) states that all of its zeros are imaginary numbers (in other words, that z = e–β lie in the unit circle) [22]. Of course, the zeros are important physically because phase transition precisely occurs around these points. The study on the zeros of zeta functions and L-functions motivated several research problems that inspired and led research in number theory in the 20th century, including the Weil conjectures, a finite field analog of the Riemann hypothesis that led to the innovations in algebraic geometry by Alexander Grothendieck and the Ramanujan “
associated to the automorphic form Δ(z) := e2𝜋iz Another interesting point is that the research on the distribution of angles (complex argument) of the Ising model with infinite site number |Λ| appears to be similar to the Sato–Tate conjecture regarding the distribution of angles of the zeros of L(s, Δ). For the Sato–Tate conjecture, it is also desirable to advance beyond the holomorphic automorphic forms and arithmetic geometry considered up to now, into non-holomorphic and Maass forms, which appear in the Selberg trace formula. In our institute, Horinaga investigated non-holomorphic automorphic forms [23], and Nakahama is working on the representation theoretical aspects underlying the NCHO, with the aim of defining a multivariate version of the NCHO [24]. This latter research is an application of a particular case of Howe’s theory of dual pairs [25] (i.e., the theory of spherical harmonics), which forms the basis of the modern invariant theory and has applications to automorphic forms. Higher dimensional constructions of the NCHO may be obtained using general dual pairs [25], thus we may expect the appearance of Sigel modular forms in the study of spectral zeta functions for these generalized constructions.
References
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||