|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
Feature Articles: New Developments in Communication Science Vol. 12, No. 11, pp. 37–43, Nov. 2014. https://doi.org/10.53829/ntr201411fa7 Quantum Computing Beyond Integer Factorization—Exploring the Potential of Quantum SearchAbstractQuantum computers are novel computing devices that make effective use of quantum-mechanical phenomena, and they are expected to emerge within the next few decades. Extensive studies on them have revealed that they will be able to solve many problems significantly faster than current computers or their possible extensions. This article briefly outlines the theory and applications of quantum search to show the potential wide applicability of quantum computing. Keywords: quantum computers, quantum algorithms, quantum communication 1. IntroductionSignificant progress in computer technology has been made since Alan M. Turing, a British mathematician, invented the mathematical model of computers. State-of-the-art computers still follow Turing’s model in principle. The term classical computers refers to all current computers and their possible extensions, which are based on Turing’s model, and classical computation/algorithms refers to the computation/algorithms performed on classical computers. Quantum computers are novel computing devices that make effective use of quantum-mechanical phenomena, so their mechanism is quite different from Turing’s model (Table 1). It is therefore expected that quantum computers, which are being extensively studied all over the world, will be able to solve a variety of problems significantly faster than the intolerably long time it takes to solve them on classical computers. To solve problems on quantum computers, we need to write a series of explicit operations to be performed on the hardware of quantum computers, as in the case of current computers. Such a series of operations is called a quantum algorithm. The computation time on quantum computers heavily depends on the quantum algorithms, just as the computation time of current computers depends on the classical algorithms. It is therefore necessary to research and develop fast quantum algorithms as well as scalable and robust hardware for quantum computers.
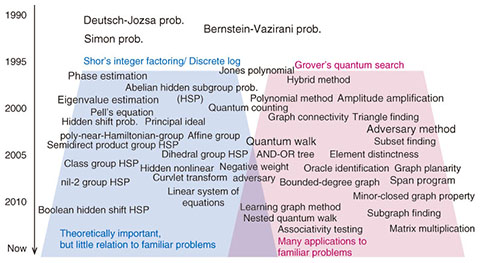
2. Fast quantum algorithms developed by Shor and GroverThe most famous quantum algorithm is arguably the one developed by Peter W. Shor in 1994 [1] that factors integers exponentially faster than any known classical algorithm. The integer factoring problem is a basic mathematical problem that is very difficult in the sense that a long history of research on this problem has not yet succeeded in finding a fast classical algorithm. In fact, the security of the RSA (Rivest-Shamir-Adelman) cryptosystem, used in practice on the Internet for secure data transmission, is based on the hardness of this problem. Shor’s discovery thus has the potential to affect a great number of people, even those outside academic communities, since it implies that quantum computers would be capable of breaking the cryptosystem. This is obviously an unhappy scenario. Extensions of Shor’s algorithm can solve hidden subgroup problems extremely quickly. In the research field of quantum algorithms, subsequent studies extended Shor’s algorithm to a collection of more general mathematical problems. Although these extensions are highly important in a theoretical sense, they seem to have little relation to the problems that are familiar to people outside the theory field, and it would thus be unlikely that those people would appreciate the extended algorithms. The quantum search algorithm (quantum search in short), developed by Lov K. Grover [2] in 1996, is also very well known. This algorithm solves the problem of finding a desired piece of data from among N pieces of data. Classical computers clearly need roughly N accesses to the data in the worst case, even if we allow a small error probability. However, the quantum search can find a desired piece of data with high probability only with approximately √N accesses. Although this cannot achieve the exponential speedups over classical algorithms, in contrast to the case of factoring integers, the quantum search can still yield a significant speedup whenever N is very large. One of the advantages in considering the search problem is that the definition of the problem is so simple that it can often emerge as a subproblem of various other problems that we want to solve. In other words, the algorithms for the problem potentially have wide applicability. One can imagine the following straightforward scenario; if one finds a search problem as a subproblem of some other problem, then one can solve the search problem significantly faster with the quantum search, which may imply a fast algorithm for the whole problem. In many cases, however, it is not an easy task to carve a search problem out of the original problem; even if one succeeds in doing so, it may be necessary to adapt the algorithm appropriately, often in a non-trivial way. This is why the search problem and its generalizations are still major topics in quantum computing research (Fig. 1).
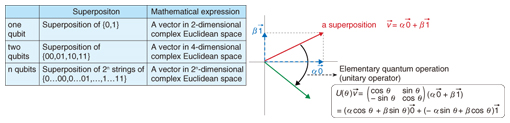
3. Quantum bits and superpositionThe unit of information on quantum computers is called a quantum bit, or a qubit. A qubit represents any superposition of 0 and 1, including 0 or 1 as a special case (Fig. 2). Similarly, two qubits represent any superposition of 00, 01, 10, and 11. Moreover, n qubits represent any superposition of 2n bit-strings: 0…0 through 1…1. The superposition is called the quantum state over the qubits. In terms of linear algebra, we can describe it as follows: Consider a two-dimensional complex Euclidean space with two orthogonal basis vectors,
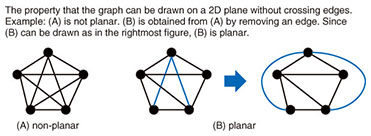
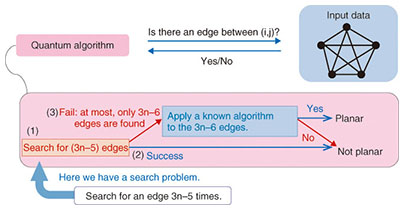
4. The search problem and quantum algorithmsTo solve a problem such as the search problem that depends on N input data X1, …, XN, we need to access the input data. Formally, we can think of this as follows: We receive Xk by making a query with the index k. We call such a query a classical query. On quantum computers, the index associated with a query is expressed with qubits, and thus a query, in this case called a quantum query, will be a superposition of classical queries over all indices k ranging from 1 to N; accordingly, the answer to the quantum query will be the corresponding superposition of all Xk, where k ranges from 1 to N. With the ability to make quantum queries, the quantum search may be stated as follows (we assume for simplicity that each piece of input data is either 0 or 1, but this is not essential to the quantum search). Theorem (Quantum Search) Given N input data X1, …, XN ∈ {0,1}, there exists a quantum algorithm that finds an index i with Xi = 1 with high probability by making approximately √N data accesses (i.e., quantum queries). To estimate the total number of steps required to solve a problem, it is necessary to count the number of steps taken to process the input data obtained via queries, as well as the number of accesses to the input data. However, we will focus only on the number of accesses to the input data, since it is a dominant factor in the search problem and the other problems dealt with in this article. As an application of the theorem, let us consider the problem of testing the planarity of a given graph. Example 1: Graph planarity testing We say that a graph is planar if the graph can be drawn without crossing any pair of edges on a two-dimensional plane (Fig. 3). It is well known that a lot of graph-theoretic problems that are hard for general graphs can be solved efficiently on planar graphs. Testing the planarity of graphs is hence one of the particularly important problems in testing graph properties. Let us define our problem more formally. We assume that graph G is an undirected graph*2 consisting of n vertices. The input data are given as the information consisting of whether an edge exists between each pair of vertices, more concretely, the set of Xij defined as follows; For each i = 1, …, n and j = 1, …, n with i < j, define Xij = 1 if there is an edge between (i, j), and Xij = 0 otherwise (that is, Xij is the (i, j)-element of the adjacency matrix*3 of G). The problem is determining with high probability if the graph represented by these ½n(n − 1) pieces of data, Xij, is planar. The key tool for carving out a search problem is a very old theorem discovered by Euler in the 18th century.
Theorem: If a graph with n vertices is planar, then the graph has at most 3n − 6 edges. With this theorem, we divide the problem into the following subproblems (Fig. 4).
(1) Identify 3n − 5 edges from among the ½n(n − 1) candidates of edges (in particular, this means identifying all edges, if the graph has at most 3n − 6 edges). (2) If Step (1) identifies exactly 3n − 5 edges, the graph is not planar according to Euler’s theorem, since 3n − 5 > 3n − 6. (3) If Step (1) identifies at most 3n − 6 edges, all edges have been identified; then, without further queries, determine whether the graph is planar with a known algorithm. Note that only Step (1) makes queries. With a little more thought, it is possible to see that Step (1) can be realized by solving 3n − 5 times the problem of searching for an edge. We can hence speed up Step (1) with the quantum search (plus some modifications). Consequently, we can prove that roughly n1.5 quantum queries are sufficient to test the planarity of a graph on quantum computers, while nearly n2 classical queries are required on classical computers [3]. We should emphasize that the key to carving out a search problem is the effective use of a theorem in the field of graph theory. There are many other important properties for which quantum speedups can be achieved, examples of which include testing graph connectivity*4 and determining the existence of Hamiltonian paths*5.
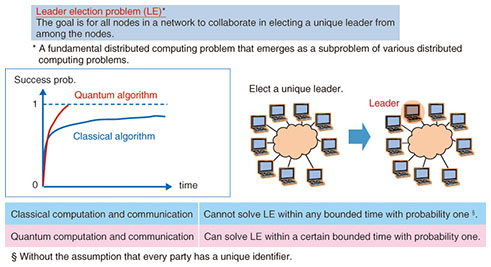
5. A generalization of quantum searchLet us sample a piece of input data at random on a classical computer. In other words, we choose a piece of data from among X1, … XN uniformly at random and access it. If there is exactly one desired piece of data among the N input data, the probability that a randomly chosen piece is the desired one is only 1/N. In fact, very roughly speaking, what the quantum search does is to iterate this random sampling in superposition √N times. Note that amplifying the success probability 1/N of the random sampling nearly to one requires roughly N times on classical computers. In this sense, we would say that the quantum search amplifies the success probability nearly to one with substantially fewer iterations. This viewpoint can be stated more generally as follows. Theorem (Quantum Amplitude Amplification [4]) Consider a classical algorithm that solves a problem with probability p by accessing input data c times. Then, it is possible to construct a quantum algorithm that solves the problem with a probability close to one by accessing input data roughly c/√p times. Moreover, if the exact value of p is known, it is possible to amplify the probability to one. In the case of random sampling for the search problem, the parameters will be c = 1, p = 1/N. The resulting quantum algorithm thus accesses the input data (roughly) c/ = √p√N times. This means that a special case of the theorem is Grover’s algorithm. Intuitively, the theorem says that roughly 1/√p iterations of the base classical algorithm in superposition can amplify the success probability p nearly to one. A similar idea can be applied to even distributed algorithms on a quantum network*6 consisting of multiple quantum computers. Example 2: The leader election problem The leader election problem is a fundamental problem in the distributed computing field in that it often appears as a subproblem of various distributed computing problems. The goal of the problem is to elect a unique leader from among all nodes in a network (Fig. 5). The problem is seemingly easy, but in the most general case where each node does not necessarily have a unique identifier, it is mathematically proved that the problem cannot be solved within any bounded time with probability one by using classical computation and communication (i.e., sending/receiving bits through communication channels). In contrast, we proved that, if quantum communication and computation can be used, the problem can be solved within a certain bounded time with probability one [5]. This means that classical distributed computing and its quantum counterpart are qualitatively different. The first proof of our result did not use the quantum amplitude amplification, but an idea of another proof that employs the quantum amplitude amplification is given as follows.
First consider the following simple classical algorithm: (1) Every node flips a coin; (2) the algorithm succeeds only when there is exactly one node that sees heads, in which case, the node will be elected as a leader. We can easily see that the success probability of this algorithm is p = n/2n , where n is the number of nodes. Since we know the exact value of the success probability, we can construct a quantum algorithm that amplifies the success probability to one by repeating the coin flipping roughly 1/√p = √2n/n times together with the quantum amplitude amplification. In fact, a much more sophisticated version of this idea flips coins roughly n times.
6. ConclusionThe development of quantum computation theory has progressed significantly in the last two decades. Recent research on quantum algorithms shows rich connections with classical computer science; state-of-the-art quantum search algorithms stem from (the quantum version of) random walk*7 or semidefinite programming*8, which are major technical tools in classical computer science. These connections will make it possible to make progress in both quantum and classical computer science in a collaborative way. Moreover, it is obviously important to study how to transform the high-level description of a quantum algorithm into a low-level description, i.e., a quantum circuit. A lot of fundamental techniques for this transformation have been intensively studied as well (e.g., [6]). Nevertheless, there are still a lot of fundamental problems to be solved before we can gain a deeper understanding of the potential power of quantum computing. To solve these problems and acquire new knowledge, we need to develop more novel techniques by making the best use of various ideas in related fields such as mathematics, physics, and classical computer science.
References
|
|||||||||||||||||||||||||||||