Regular Articles

Vol. 19, No. 3, pp. 53–62, Mar. 2021. https://doi.org/10.53829/ntr202103ra1

Increasing Capacity of a Strictly Non-blocking Clos Network Composed of Optical Switches

Toru Mano, Takeru Inoue, Kimihiro Mizutani, and Osamu Akashi

Abstract

Clos networks are widely used due to their non-blocking property. However, in strictly non-blocking Clos networks composed of ordinary optical switches (switches with equal numbers of input/output ports), we find that a substantial number of ports can remain unused, which decreases their efficiency. This inefficiency comes from the implicit restriction that the two sides of switches have distinct roles, i.e., ports on one side are connected to endpoints (terminals) while those on the other side are linked to switches. Removing this restriction provides greater freedom in constructing a network and can increase capacity without losing the strictly non-blocking property. We propose a new strictly non-blocking network and provide several theorems that address network capacity. Numerical experiments show that the proposed network has up to 30% more capacity compared with a strictly non-blocking Clos network.

Keywords: non-blocking switching networks, Clos network, network design

1. Introduction

Constructing non-blocking switching networks [1], where connections can be established between any pair of idle ports, remains a vital issue in the field of network design. Such networks have been applied in many areas such as telephone networks [2], asynchronous transfer mode networks [3], optical switching with wavelength-division multiplexing technologies [4], and time-division packet switching [5]. A rich body of literature has been produced on non-blocking networks with the goal of constructing larger-capacity networks [6, 7]. Clos networks [2] are classic networks, and their capacity has been extensively analyzed [8], e.g., 10,000 connections can be accommodated using 59 2000-port switches arranged in a three-stage network.

To the best of our knowledge, studies on non-blocking networks made the implicit restriction that switches have two facing sides with several ports, and only one side can be used to connect to endpoints [9, 10]. For example, in Fig. 2, for switches in the input layer, the left side is connected to endpoints (t’s) while the right side is linked to switches. This restriction makes it easy to understand the network, but it might decrease the efficiency of a Clos network if it consists of ordinary square switches (switches with equal numbers of input/output ports) [11, 12]. As discussed in Section 3, a substantial number of ports has to remain unused in a Clos network, e.g., in Fig. 2, if unused (black) ports are connected, the capacity would not increase or the network would lose its non-blocking property.

We focus on a non-blocking switching network with greater capacity than the Clos equivalents. To increase capacity, we remove the above implicit restriction while still using square switches, which have equal numbers of input/output ports, as used in previous studies [9, 10]. To the best of our knowledge, this is the first study on maximizing the capacity of non-blocking networks that use square switches without the above restriction. Among the several known non-blocking properties [1], we investigated non-blocking networks in the strict sense (any idle port can be connected independent of current connections) with the most fundamental form of space-division multiplexing^*1. Note that we focus on networks with only a single intermediate layer to mitigate signal attenuation. Since our focus is on the strict non-blocking property, routing issues are not discussed.

The contributions of this article are summarized as follows.

Section 3 reveals that a substantial number of ports can remain unused in Clos networks.
Section 4.1 proposes a strictly non-blocking network that is based on a Clos network.
Section 4.2 proves that the proposed network has equal or larger capacity than a Clos network.
Numerical evaluations with reasonable parameters showed that the proposed network has up to about 30% larger capacity than a Clos network (Section 5).

*1	Extension to time-division, wavelength-division, and code-division multiplexing [7] is for our future work.

2. Preliminaries

2.1 Problem statement

The basic switching component is represented as a square switch, as illustrated in Fig. 1. A square switch has two sides, and each side has N ports. Although input and output ports can coexist on the same side, we are only allowed to connect an input port on one side with an output port on the other side. We assume that all switches have equal N. The size of a square switch is defined as N.

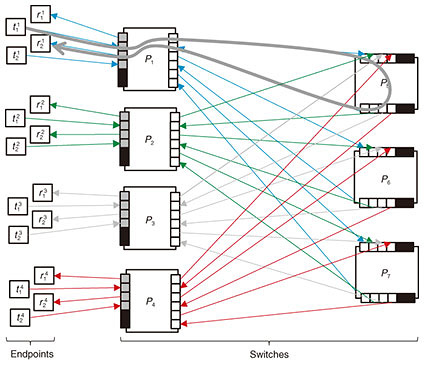
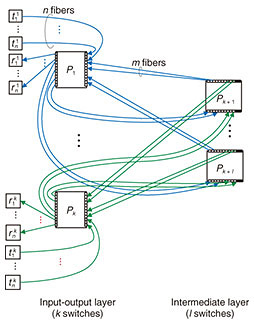
Fig. 1. All four possible configurations in a square switch of N = 4.

A switching network is defined as a set of switches connected by directional links (optical fibers), and the network is connected to endpoints, as illustrated in Fig. 2. Ports connected to an endpoint are called external ports, while the other ports are called internal ports. Ports without links are called unused ports. Since links have a direction, all external/internal ports and endpoints are classified as either transmitting or receiving. Every transmitting port/endpoint is allowed to connect only with a receiving one. We consider switching networks with a single layer of intermediate switches (intermediate switches are those without external ports) such as one-sided two-stage (Fig. 2 and Fig. 3) and two-sided three-stage (Fig. 4) networks.

Fig. 2. An example of strictly non-blocking switching network (N = 6). External switch ports are gray, internal switch ports are white, and unused ports are black.

Fig. 3. A folded Clos network consisting of k + l switches. This network offers up to n ・ k connections.

Fig. 4. An unfolded Clos network consisting of 2k + l switches. This network offers up to n ・ k connections.

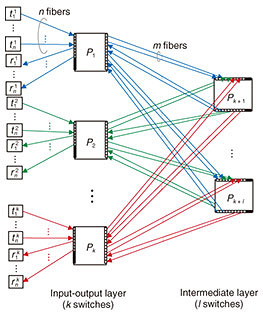
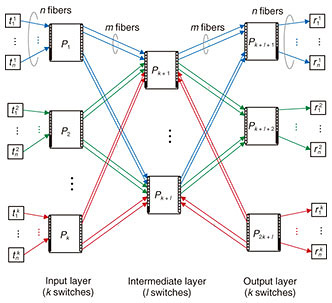
Connection requests are classified into two categories: creation and termination. A creation request, specified by a pair of idle endpoints, triggers the establishment of a path between the endpoints. In Fig. 2, two endpoints and are specified, and the thick gray line represents the path established between them. A termination request, which specifies an existing connection, releases the corresponding path. Note that the request sequence is unknown in advance.

Strictly non-blocking networks are designed to accept any request sequence without requiring the rearrangement of existing paths. Moreover, paths used to satisfy creation requests should be chosen arbitrarily. Thus, the path-selection algorithm is outside the scope of this article.

Our problem, the connection maximization problem, is defined as follows. Given the number of switches, construct a strictly non-blocking network that has the maximum number of connections. This maximum number of connections is the capacity of the network. In Fig. 2, given seven switches, eight connections can be established between the eight transmitting endpoints and eight receiving endpoints.

2.2 Current approach: Clos networks

This subsection reviews current non-blocking networks, i.e., their connection schemes, non-blocking conditions, and formulations of the connection maximization problem. We explain two current Clos networks: unfolded Clos [2, 6, 9] and folded Clos [7, 10]. Note that an unfolded Clos network is usually called just a Clos network, but to eliminate the ambiguity between folded and unfolded, we explicitly call it an unfolded Clos network. The disadvantages of these networks are analyzed in Section 3. These networks are similar, but they have different capacities, as discussed in Section 5.

As explained in the Introduction, these networks have an implicit restriction; ports on one side are either all external or all internal; mixing is not permitted.

2.2.1 Folded Clos networks

Figure 3 illustrates a folded Clos network [7, 10]. A folded Clos network has k > 2 switches in the input-output layer and l switches in the intermediate layer. The case of k ≤ 2 is ignored because it can support at most N connections, and a single switch is sufficient. The right side of each switch in the input-output layer is connected to each side of the switches in the intermediate layer with m fibers. The left side of each switch, P_i, in the input-output layer is connected to n transmitting endpoints, {} j = 1,…, n, and n receiving endpoints, {} j = 1,…, n. Hence, a folded Clos network can serve n · k connections in total. In Fig. 3, substituting 4, 3, 1, 2 with k, l, m, n, respectively, yields the network in Fig. 2.

The network is strictly non-blocking if and only if [7]

Therefore, as illustrated in Fig. 2, if we increase the number of external ports, n, to 3 from 2, i.e., 3 transmitting external ports and 3 receiving ones, then the network loses its strictly non-blocking property.

In folded Clos networks that use at most a switches with N ports, the maximum number of connections, i.e., the capacity 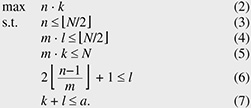(a; N) can be obtained by solving the following problem over positive integer variables k(> 2), l, m, n ∈ .

Objective (2) represents the number of connections in a folded Clos network, and Constraints (3), (4), and (5) infer that each side of the switch has enough ports for fiber provision. Constraint (6) guarantees the non-blocking property, and Constraint (7) restricts the number of switches used. We say the connection parameters (k, l, m, n) are feasible for a folded Clos network if they satisfy Constraints (3), (4), (5), and (6).

2.2.2 Unfolded Clos networks

Figure 4 illustrates an unfolded Clos network [2, 6, 9]. Its connection scheme is similar to that of folded Clos networks. We consider only k > 1 for the same reason given for folded Clos networks.

This network is strictly non-blocking if and only if [6]

As with a folded Clos network, the maximum number of connections, i.e., the capacity (a; N), can be obtained by solving the following problem over positive integer variables k(> 1), l, m, n ∈ .

3. Disadvantages of using Clos networks

This section explains the disadvantages of Clos networks. Moderately sized strictly non-blocking folded Clos and unfolded Clos networks must have relatively large numbers of unused ports.
Proposition 1. Let s be an integer greater than 1. A strictly non-blocking folded Clos network that can serve at least sN connections has at least N unused ports on the left side of the input-output switch. That is, if connection parameters (k, l, m, n) are feasible for this network and satisfy nk ≥ sN, then N − 2n ≥ N.
Proof. Let (k, l, m, n) be feasible connection parameters with nk ≥ sN. We have k ≥ 2s because of Constraint (3) and condition nk ≥ sN. Let q be an integer such that q = , then we have n ≤ (q + 1)m and 2q + 1 ≤ l from Constraint (6). Together with Constraints (4) and (5), we have 2n ≤ (l + 1)m ≤ 2n ≤ (l + 1)m ≤ N.
Proposition 2. Let s be an integer greater than 1. A strictly non-blocking unfolded Clos network that can serve at least sN connections has at least N unused ports on the left/right side of the input/output switch. That is, if connection parameters (k, l, m, n) are feasible for this network and satisfy nk ≥ sN, then N − n ≥ N.
Proof. Let (k, l, m, n) be feasible connection parameters with nk ≥ sN. We have k ≥ s because of Constraint (10) and condition nk ≥ sN. Let q be an integer such that q = , then we have n ≤ (q + 1)m and have 2q + 1 ≤ l from Constraint (6). Together with Constraints (11) and (12), we have n ≤ = N.

The above propositions show that the capacity of folded Clos or unfolded Clos networks increases and more ports are unused: the number approaches asymptotically. This was also observed through the numerical evaluation discussed in Section 5.

4. Proposed network

In this section, we explain the proposed network that is based on folded Clos networks. First, we explain the proposed network and its non-blocking condition. We then compare its capacity with that of Clos networks from the theoretical viewpoint.

4.1 Proposed network and its non-blocking condition

Figure 5 illustrates the proposed network. Both sides of the input-output layer are connected to endpoints. At the left side of each switch in the input-output layer, n ports are connected to receiving endpoints, while every m port is connected to the down side of a switch in the intermediate layer. The right side mirrors this configuration. The proposed network offers n · k connections in total. We consider only k > 2 as per a folded Clos network. We confirmed that the construction of the proposed network is feasible on commercially available optical switches.

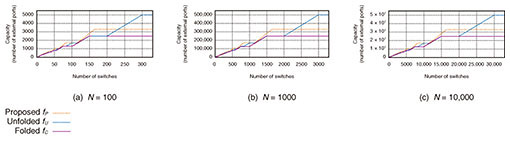
Fig. 5. The proposed switching network consisting of k + l switches. This network offers up to n ・ k connections.

The strictly non-blocking condition, Condition (1), does not change, and the proof is almost the same as for a Clos network [2, 6] (the proof is given at the end of this subsection).
Proposition 3. The proposed network is strictly non-blocking if and only if

The maximum number of connections, i.e., the capacity 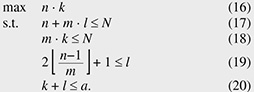(a; N), can be obtained by solving the following problem on positive integer variables k(> 2), l, m, n ∈ .

Compared to a folded Clos network, the constraints related to input-output square switch size, i.e., Constraints (3) and (4), are replaced with Constraint (17). The other constraints are the same.

As discussed in Section 5, the proposed network has less unused ports compared with current networks because the proposed network does not have the implicit restriction, that is, a single side in the proposed network can have both external and internal ports.

Finally, we give a proof of Proposition 3.
Proof of Proposition 3. First, we discuss sufficiency. Without loss of generality, we can assume that a connection-creation request has arrived. Because P₁ uses at most n−1 fibers connected to transmitting endpoints, at most n−1 fibers that go to intermediate switches from P₁ are used. With the same argument, at most n−1 fibers that come to P₂ from intermediate switches are used. Hence, at most intermediate switches run out of available fibers that come from P₁, and at most intermediate switches run out of available fibers that go to P₂. Thus, if we have 2 +1 intermediate switches, there exists at least one intermediate switch that has an available fiber coming from P₁ while another one goes to P₂. By using this intermediate switch, we can establish the connection.

Next, we discuss necessity. Suppose l is 2, and connection-creation requests {}i = 1,…, n–1 and {}i = 1,…, n–1 have arrived; the former requests {} use the first l/2 intermediate switches, and latter requests {} use the last l/2 intermediate switches. Note that a strictly non-blocking network has to establish a connection between idle ports regardless of the past path selection. However, connection-creation request cannot occur because the first l/2 intermediate switches do not have any available fiber coming from P₁ and the last l/2 intermediate switches do not have any available fiber going to P₃.

4.2 Capacity comparison

This subsection compares capacity from a theoretical viewpoint. We show that the proposed network has equal or larger capacity than a folded Clos network (Theorem 1). With regard to an unfolded Clos network, we give only a sufficient condition for the proposed network to have equal or larger capacity (Theorem 2). Due to the complexity of the discrete nature of integers, it is intractable to analyze the remaining case, i.e., the case that Theorem 2 does not cover. To compare the remaining case, we conducted a numerical evaluation, as discussed in Section 5.

First, we prove that the capacity of the proposed network (a; N) is greater than or equal to that of a folded Clos network (a; N).
Theorem 1. The proposed network has equal or larger capacity than a folded Clos network. That is, we have

when there is a feasible solution for a folded Clos network.
Proof. Suppose that the connection parameters (k, l, m, n) are feasible for a folded Clos network. That is, (k, l, m, n) satisfy Constraints (3), (4), (5), (6), and (7). Then, it is sufficient to show that (k, l, m, n) are also feasible for the proposed network. The only difference between the proposed and folded Clos networks is that a folded Clos network has Constraints (3) and (4), whereas the proposed network has Constraint (17). We have

≤ N. Since Constraints (3) and (4) infer another Constraint (17), (k, l, m, n) are also feasible for the proposed network.

Next, we give a sufficient condition for the proposed network to have equal or larger capacity to an unfolded Clos network.
Theorem 2. If one of the optimal configurations of an unfolded Clos network has even m, then the proposed network has equal or larger capacity, i.e., (a; N)(a; N) ≤ (a; N), where m is the number of connections between the input/output switches and intermediate switches.

To prove Theorem 2, we use the following proposition and lemma. First, we give a proof of the lemma, then provide a proof of the proposition, and finally prove Theorem 2.
Proposition 4. Let (k, l, m, n) be feasible for an unfolded Clos network and m be an even integer. There exist feasible parameters (k’, l’, m’, n’) for the folded Clos network such that nk ≤ n’k’ and 2k + l ≥ k’ + l’.
Lemma 1. Let (k, l, m, n) be feasible for an unfolded Clos network, m be an even integer, and n be an odd integer. Parameters (k, l, m, n+1) are also feasible for the unfolded Clos network.
Proof of Lemma 1. Let q be an integer such that q = . It is sufficient to show n+1 ≤ N and = q. Since n is odd and m is even, we have qm + 1 ≤ n ≤ m(q+1) − 1. This inequality gives us = q. In addition, since Constraint (11) is satisfied, we have n+1 ≤ m(q+1) ≤ m(2q+1) ≤ ml ≤ N.
Proof of Proposition 4. Due to Lemma 1, we can assume that n is also even. Hence, it is sufficient to show that (k’, l’, m’, n’) = are also feasible for the folded Clos network. That is, we show that (k’, l’, m’, n’) satisfy Constraints (3), (4), (5), and (6). Since m and n are even, Constraints (3), (4), and (5) are satisfied. Let us consider the remaining constraint, Constraint (6). Let q be an integer such that q = , then by using integer r ∈ {0, 1, ..., m−1}, n can be represented as n = mq + r +1. By dividing by 2 and subtracting 1, we have n’–1 = m’q + (r+1)/2 − 1. Since m and n are even, the residue (r+1)/2 − 1 is one of {0, 1, ..., m’−1}. Hence, we have + 1 = l'.
Proof of Theorem 2. We prove the theorem by contradiction using Theorem 1 and Proposition 4. Suppose that there exists a configuration of an unfolded Clos network with even m that has a larger capacity than the proposed network. Then, by Proposition 4, we can convert this unfolded Clos network into a folded Clos network without losing capacity. Hence, the converted folded Clos network has larger capacity than the proposed network. However, this contradicts Theorem 1.

5. Numerical evaluation

This section numerically compares the proposed network with folded and unfolded Clos networks^*2. We now show that the proposed network has improved capacity.

First, we show that switch size slightly affects the results. Figure 6 shows the capacity (y-axis) and number of switches used (x-axis). We plot the results for the folded Clos, unfolded Clos, and proposed networks, that is, (a; N), (a; N), and (a; N). We used three switch sizes, N = 100 (Fig. 6(a)), 1000 (Fig. 6(b)), and 10,000 (Fig. 6(c)). All three cases generated almost identical plots. We confirmed that other switch sizes, N ∈ {200, 300, ..., 900} {2000, 3000, ..., 9000}, generated almost identical plots. These results imply that switch size slightly affects capacity comparison. Note that, in the folded Clos, unfolded Clos, and proposed networks, the line became flat when a exceeded around 3/2N, 3N, and 5/3N, respectively. The reason is that capacity does not increase even if we add more available switches since we run out of internal ports that the switches can use to connect with each other. One way to evade this situation is adding another intermediate layer. However, as explained in Section 2.1, we considered networks with a single intermediate layer. Extension to multistage networks is for future work.

Fig. 6. The capacity and number of switches used. We examined three square switch sizes N = 100 (a), 1000 (b), and 10,000 (c). All three cases generated almost identical plots.

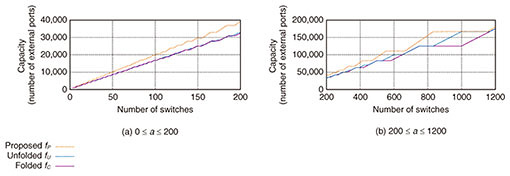
Next, we compared the capacity of the proposed network with folded Clos and unfolded Clos networks. We investigated plots for a certain switch size since, as we saw above, the switch size slightly affects the plots. We chose N of 1000. Figure 7 is an enlargement of Fig. 6(b), i.e., replots the curves with smaller ranges of a, since it is difficult to tell the difference among the three lines from Fig. 6(b) when a is relatively small. Figures 7(a) and 7(b) illustrate the plots for 0 ≤ a ≤ 200 and for 200 ≤ a ≤ 1200, respectively. These three figures show that the proposed network has equal or larger capacity than the folded Clos network and that the proposed network has equal or larger capacity than the unfolded Clos network if a ≤ 2.3N. In fact, the proposed network has up to about 30% more capacity. For example, when the number of available switches a is 833, the capacity of a folded Clos network is 125,000 with (k, l, m, n) = (500, 249, 2, 250), and that of an unfolded Clos network is 125,250 with (k, l, m, n) = (250, 333, 3, 501), whereas that of the proposed network is 167,000 with (k, l, m, n) = (500, 333, 2, 334). 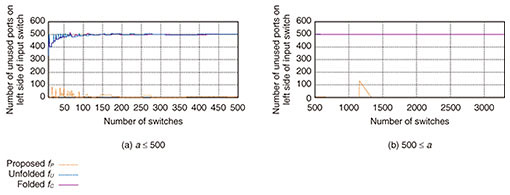We also compared capacity using other switch sizes, N ∈ {200, 300, ..., 900} {2000, 3000, ..., 9000} and confirmed that the proposed network has equal or larger capacity than an unfolded Clos network if a ≤ 2.3N.

Fig. 7. The capacity and number of switches used for smaller a. These plots were obtained by enlarging Fig. 6(b).

Finally, we compared the number of unused ports on the left side of the input switch; those of a folded Clos, unfolded Clos, proposed networks are N−2n, N−n, N−n−ml, respectively. Figure 8 shows the number of unused ports when N = 1000. In the folded Clos and unfolded Clos networks, almost half the ports remained unused, whereas, in the proposed network, the number of unused ports was less than 10 in more than 90% of a ≤ 3000. The largest number of unused ports was 134 when a = 1155. At this point (a = 1155), m of the optimal connection parameters decreased to 1 from 2, and this change made some ports unused. We also compared the number of unused ports using other switch sizes and obtained similar results.

Fig. 8. The number of unused ports on the left side of the input switch and number of switches used when N = 1000.

The capacity of an unfolded Clos network matches that of a folded Clos network. For example, let the switch size be N =100 and the number of switches be one of {8, 9, ..., 12}. Then the unfolded Clos network has larger capacity for a = 8, 12, and the folded Clos network has larger capacity for a = 9, 10, 11.

6. Related work

A Clos network is one of the most commonly used non-blocking networks [1, 2, 6]. Many studies have examined non-blocking properties under various switching environments. There are four non-blocking properties; strictly [2], wide-sense [6], re-arrangeably [1], and re-packably [7]. The wide-sense property allows us to select which path is used to establish a new connection. Under the strict property, the path is arbitrarily chosen. The latter two enable us to rearrange existing paths to establish connections. We focused on strictly non-blocking networks because wide-sense non-blocking fails to significantly increase capacity if at all [6], and the latter two types require the movement of existing connections, which triggers network outages during path reconfiguration.

7. Conclusion

This article proposed a non-blocking network composed of square switches such as optical switches and confirmed that it has a larger capacity than Clos networks. Our network has up to about 30% more capacity under reasonable parameters. Future work includes investigating routing algorithms on our network and extensions to multiple intermediate layers.

References

[1]	V. Beneš, “Mathematical Theory of Connecting Networks and Telephone Traffic,” Academic Press, New York, 1965.
[2]	C. Clos, “A Study of Non-blocking Switching Networks,” Bell System Technical Journal, Vol. 32, No. 2, pp. 406–424, Mar. 1953.
[3]	J. Turner and R. Melen, “Multirate Clos Networks,” IEEE Commun. Mag., Vol. 41, No. 10, pp. 38–44, Oct. 2003.
[4]	E. Oki, N. Yamanaka, K. Nakai, and N. Matsuura, “Multi-stage Switching System Using Optical WDM Grouped Links Based on Dynamic Bandwidth Sharing,” IEEE Commun. Mag., Vol. 41, No. 10, pp. 56–63, Oct. 2003.
[5]	H. J. Chao, Z. Jing, and S. Y. Liew, “Matching Algorithms for Three-stage Bufferless Clos Network Switches,” IEEE Commun. Mag., Vol. 41, No. 10, pp. 46–54, Oct. 2003.
[6]	F. Hwang, “The Mathematical Theory of Nonblocking Switching Networks,” 2nd Edition, World Scientific, Vol. 15, 2004.
[7]	W. Kabacinski, “Nonblocking Electronic and Photonic Switching Fabrics,” Springer, 2005.
[8]	A. Jajszczyk, “Nonblocking, Repackable, and Rearrangeable Clos Networks: Fifty Years of the Theory Evolution,” IEEE Commun. Mag., Vol. 41, No. 10, pp. 28–33, Oct. 2003.
[9]	A. Jajszczyk, “A Dynamic Programming Approach to Optimization of Switching Networks Composed of Digital Switching Matrices,” IEEE Trans. Commun., Vol. 35, No. 12, pp. 1342–1346, Dec. 1987.
[10]	A. Jajszczyk and W. Kabacinski, “Rearrangeable One-sided Switching Networks Composed of Uniform Time-space Elements,” Electron. Lett., Vol. 21, No. 7, pp. 285–286, Mar. 1985.
[11]	R. Spanke, “Architectures for Large Nonblocking Optical Space Switches,” IEEE J. Quantum Electron., Vol. 22, No. 6, pp. 964–967, June 1986.
[12]	A. S. Kewitsch, “Large Scale, All-fiber Optical Cross-connect Switches for Automated Patch-panels,” J. Lightw. Technol., Vol. 27, No. 15, pp. 3107– 3115, Aug. 2009.

	Toru Mano Researcher, NTT Network Innovation Laboratories. He received a B.E. and M.E. from the University of Tokyo in 2009 and 2011. He joined NTT Network Innovation Laboratories in 2011. He received a Ph.D. in computer science and information technology from Hokkaido University in 2020. His research interests are network architectures and network optimization. He is a member of the Operations Research Society of Japan (ORSJ).
	Takeru Inoue Senior Researcher, NTT Network Innovation Laboratories. He received a B.E. and M.E. in engineering science and a Ph.D. in information science from Kyoto University in 1998, 2000, and 2006. He was an ERATO Researcher with the Japan Science and Technology Agency from 2011 to 2013. His research interests cover algorithmic approaches in computer networks. He was a recipient of the Best Paper Award of the Asia-Pacific Conference on Communications in 2005. He is a member of the Institute of Electrical and Electronics Engineers (IEEE).
	Kimihiro Mizutani Lecturer, Department of Informatics, Kindai University. He received an M.S. and Ph.D. in engineering from the Nara Institute of Science and Technology, in 2010 and 2015. He was a researcher at NTT Network Innovation Laboratories and NTT WEST R&D Center from 2010 to 2019. His research interests include future network architectures and various systems powered by deep learning. He was a recipient of the Best Student Paper Award from ICCSA in 2010 and the Research Awards from IEICE in 2013. He is a member of the Institute of Electrical Engineers of Japan (IEEJ).
	Osamu Akashi Research Professor, Research and Development Center for Academic Networks, National Institute of Informatics. He received a B.Sc. and M.Sc. in information science and a Ph.D. in mathematical and computing sciences from the Tokyo Institute of Technology, in 1987, 1989, and 2001. He was a Senior Research Scientist in NTT Network Innovation Laboratories from 2001 to 2018. His research interests are in distributed systems, network management, and network architecture. He is a member of the Association for Computing Machinery (ACM), Information Processing Society of Japan (IPSJ), and Japan Society for Software Science and Technology (JSSST).

↑ TOP