|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
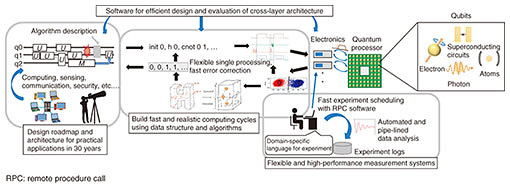
Feature Articles: Toward New-principle Computers Vol. 19, No. 5, pp. 40–44, May 2021. https://doi.org/10.53829/ntr202105fa6 Fault-tolerant Technology for Quantum Information Processing and Its Implementation MethodsAbstractTo use quantum information processing in a wide range of applications, fault-tolerant processing is essential to cope with noise. Fault-tolerant quantum computing using quantum error-correcting codes is scalable, but the overhead of number of qubits or processes is large, so improving efficiency is an important research theme. Quantum error mitigation incurs computational cost, but it does not require the overhead of number of qubits, so it is expected to be used for near-future applications. In this article, we introduce our research activities on these topics as well as our studies toward the implementation of quantum information processing. Keywords: quantum information processing, error correction, error mitigation 1. IntroductionThe potential of quantum computers and quantum networks has been attracting attention recently. Fault-tolerant processing is the most essential technology for this because there is a significant difference in the amount of noise that can occur between quantum information processing and current information processing (classical information processing). In classical information processing, errors occur less frequently, so most information processing can be done without much concern for errors. However, in quantum information processing, errors occur so frequently that only small-scale computations can be executed without handling the errors. To make quantum information processing scalable, execute various useful quantum computations, and develop a large-scale quantum network, it is necessary to carry out fault-tolerant processing for quantum information and protect quantum information from noise. In quantum information processing, therefore, fault tolerance is expected to become a fundamental part of computer and network architecture technology. We are investigating fault-tolerant processing as an important fundamental technology to protect quantum information from errors and noise. There are two major error-suppression methods for quantum information processing: using quantum error-correcting codes and quantum error mitigation. Quantum error-correcting codes redundantly encode one logical qubit into multiple physical qubits that can be corrected by decoding even if some errors occur. Fault-tolerant quantum computing using quantum error-correcting codes is the only method known to be capable of scalable quantum computing with fault tolerance and is expected to be essential for the practical application of large-scale quantum information processing in the future. However, the number of qubits and processes required for encoding and decoding will inevitably increase; therefore, it will take a long time to achieve large-scale fault-tolerant quantum computing. Another method that has been attracting attention recently is the quantum error-mitigation method. This is a method of removing errors from the computational results by predicting the correct calculation results without the overhead of number of qubits. Computational cost increases exponentially with the noise level for the prediction of the error-free results; hence, this is not scalable. However, it does not require the overhead of number of qubits, so it is considered an important method while the scale of quantum information processing is still small. It is also important that the elemental quantum gates be as accurate as possible and have high functionality for communication and distributed processing. We introduce our research activities on software infrastructure for fault-tolerant quantum computing, quantum error-mitigation methods, and basic elements for the implementation of quantum information processing. 2. Research and development for fault-tolerant quantum computingQuantum computers enable various types of novel information processing by using the superposition of quantum states but at the cost of being vulnerable to noise and slow throughput of unit instructions. In current memories, such as dynamic random access memory, a capacitor is charged or discharged to indicate 0 or 1, and under threshold operation with a sufficient margin, the memory is refreshed earlier than the information is lost by natural discharge. This mechanism enables long-time storage of information with a small overhead. In comparison, quantum memories using a superconducting circuit, which also manipulates electrons, are not only slow in executing basic operations but also cannot be directly refreshed due to the no-cloning theorem. This problem can be avoided by encoding information of qubits using quantum error-correcting codes and by repeatedly detecting and correcting errors indirectly. However, carrying out quantum computations with quantum error correction requires enormous resources: hundreds or thousands of times more in time and size than that without error correction [1]. Thus, in developing quantum computers, the loss of information from a volatile memory must be suppressed by fast feedback with error-correcting codes instead of a simple refresh. To develop a practical fault-tolerant quantum computer, it is essential to construct a system with not only excellent quantum devices but also scalability, broadband interfaces, and robust control. Our group, in collaboration with RIKEN and several universities, is developing a fault-tolerant quantum computer using superconducting qubits with both high performance and high reliability. In this section, we introduce three topics on the software infrastructure of quantum computers, an overview of which is illustrated in Fig. 1.
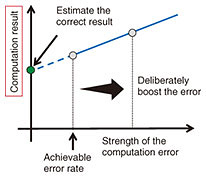
The first topic is a system to efficiently characterize and calibrate a large number of superconducting qubits on a chip. Currently, superconducting qubits must be individually controlled due to their inhomogeneity; thus, the measurement system becomes a huge distributed system consisting of a large number of field-programmable gate arrays and microwave sources. We constructed basic software for asynchronous control of such devices and automatic and fast calibration of a large number of qubits. We also proposed efficient methods for characterization and calibration using machine learning and quantum randomness [2, 3]. The second topic is the design of peripheral circuits that execute the operations and feedback required for quantum error correction. The maximum likelihood estimation of errors in a high-performance quantum error-correcting code can be reduced to a graph problem called minimum-weight perfect matching. However, naive algorithms to solve this problem are not practical since they have large latency. Our group is working on a method for optimizing decoding circuits for small codes using machine learning [4] and on a fast decoder using single-flux-quantum circuits [5]. The third topic is a software toolchain to translate programs across multiple technology layers to evaluate the performance of architectures and simulate their behavior. In particular, our quantum circuit simulator, which is a part of the toolchain, became the world’s fastest for several benchmarks [6]. As mentioned above, the development of a large-scale fault-tolerant quantum computer is a battle to control integrated quantum devices while ensuring high performance and reliability with optimized control devices and algorithms using a large-scale distributed system. This is a challenging task that is suitable for NTT laboratories, who have been studying these technologies. 3. Quantum error-mitigation methodIn October 2019, Google announced that a quantum computer was able to solve a problem that would have taken 10,000 years to solve with a classical computer in 200 seconds using a small-scale quantum device with 53 qubits [7]. Small-scale, noisy quantum computers such as the one used in this demonstration are called noisy intermediate-scale quantum (NISQ) computers. There is a counterargument that the problem solved by Google can be solved in a few days using a supercomputer, not 10,000 years. However, as the size of quantum computers becomes larger, this gap is expected to widen further. Researchers worldwide are studying how to use such small-scale quantum devices practically. They are mainly expected to be applied to chemical calculations and machine learning. However, the computational errors of such small-scale quantum computers cannot be ignored. Historically, quantum error correction has been studied as a method of suppressing errors. In quantum error correction, multiple qubits are used to encode one logical qubit, and the error is suppressed exponentially with respect to the number of qubits used for encoding. However, this method is not suitable for NISQ computers, which have a limited number of qubits. Therefore, quantum error mitigation has been extensively studied to suppress errors without increasing the burden on the hardware side [8]. Quantum error mitigation does not require the overhead in number of qubits but does require a larger number of measurements. A variety of error-mitigation methods have recently been proposed. In this section, we first explain the simplest and most straightforward extrapolation method. The computational error of a quantum computer can be increased by adding noisy operations, etc. The extrapolation method is to estimate the error-free result by extrapolating the original result and the result with the increased error. A conceptual diagram of the extrapolation method is shown in Fig. 2. There is also a method called the quasi-probability method, which identifies the error model of the computational error and executes an inverse transformation of the error to effectively cancel it [9]. There are also other methods such as the symmetry verification method and subspace expansion method. For further details, please refer to the review paper [8].
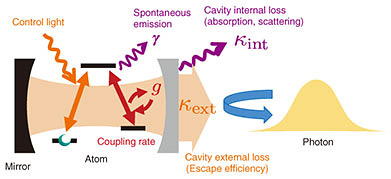
With the expectation on an increase in the number of qubits in the future, our group showed for the first time that quantum error mitigation is useful for further improving computational accuracy, even after fault-tolerant quantum computing using quantum error correction becomes possible to some extent [10], and that quantum error correction and quantum error mitigation should not be considered separately but should be considered as an integrated scheme. 4. Implementation schemes for basic elemental technologiesThus far, we have introduced how to effectively implement fault-tolerant processing from the software side for given hardware. It is also important for fault tolerance that the implementation schemes of the basic elements function with high accuracy and have scalability. It is also important that the functions become more sophisticated for communication and distributed processing. In particular, various elemental technologies based on the interaction between atoms and photons using cavity quantum electrodynamics (QED) (Fig. 3) are important for expanding the functions for quantum computing and quantum networks. NTT Secure Platform Laboratories is studying such implementation schemes for future quantum secure-network infrastructures including quantum repeaters.
It is first important to generate photons, which are used as qubits for quantum communication, with high efficiency and scalability. There are problems in scalability of current single-photon generation methods using a weak laser light or nonlinear crystals because of the unwanted multiple-photon generation events. Deterministic single-photon generation is possible with high efficiency using single-atom cavity QED systems [11]. We investigated the improvement in the repetition rate by shortening the pulse length, so that the overall performance of information processing can be improved [12]. When atoms are used as stationary qubits and photons are used as communication qubits, highly accurate quantum gates between atoms and photons are possible by using cavity QED systems. For these gates, we considered the trade-off in fault tolerance in terms of photon loss and gate fidelity and investigated implementation schemes that optimize them [13]. We are investigating circuit QED systems to efficiently execute quantum gates between superconducting qubits and microwave photons or the routing of the microwave photons for distributed processing of superconducting quantum computers [14, 15]. 5. ConclusionWe are investigating fault-tolerant quantum computing using error-correcting codes and quantum error-mitigation methods from the viewpoint of software infrastructure. We are also engaged in research from the opposite side, that is, how to improve the accuracy and efficiency of the basic elements of the physical implementation and how to expand its functionality. We are attempting to create a new efficient architecture for a sufficiently large fault-tolerant quantum computer, which is expected to be put to practical use in the far future. In the meantime, we are conducting research on making quantum information processing as meaningful as possible in the near future by using quantum error mitigation and other methods. References
|
|||||||||||||||||||||||||||||||