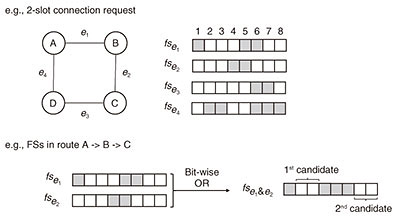
Routing and Spectrum Assignment Using Deep Reinforcement Learning in Optical Networks

1. Introduction

Internet traffic has been grown rapidly due to increasingly diversified traffic demands as a result of both video-streaming and cloud-computing services. To handle the changing requirements of future traffic in backbone networks, the concept of the elastic optical network (EON) was proposed [1]. EONs have a finely granular frequency grid (typically a multiple of either 6.25 or 12.5 GHz) to allocate the minimum frequency bandwidth to each channel, compared with the traditional flexed-grid (e.g., 50 GHz). EONs allocate a different number of frequency slots (FSs) to a connection request in accordance with the bandwidth demand for more efficient spectral utilization. However, non-uniform FS allocation results in spectral fragmentation that degrades spectral utilization. Therefore, efficient use of the spectral resources in EONs requires a routing and spectrum assignment (RSA) algorithm that can prevent spectral fragmentation.

Research into optical networking has yielded proposals based on RSA using deep reinforcement learning (DRL) [2] in EONs. The pioneering studies are on DeepRMSA [3] and its improved version [4], which determine the routing path among K shortest paths (KSPs), outperforming traditional RSA based on shortest path and KSP algorithms. These pioneering studies indicated that DRL-based RSA is promising. In this article, we introduce the basic concept of RSA in EONs followed by DRL-based RSA algorithms for efficient network planning in EONs. We then explain our proposed DRL-based RSA algorithm called Mask RSA along with its performance evaluation.

2. EONs

EONs have emerged as one of the most promising network technologies for next-generation optical networks. In simulation, an EON consists of nodes and links, and each link has FSs. FSs are represented as indexed list of FS status, e.g., available and occupied FSs are represented as 1 and 0, respectively, then FSs indicate a list [0,0,0,1,1,1,0,1,1]. Each connection request has a duration, and when the duration elapses, the FSs that were used are released.

Figure 1 illustrates an example of a simulated EON that consists of four nodes, A, B, C, and D, and four links, A-B, B-C, C-D, and D-A. Each link has eight FSs. Let us take the case of an incoming connection request from node A to node C with two FSs. To check which FSs are available to assign in the route A-B-C, FSs of links in the route are calculated by the bitwise AND operation; the FSs of A-B are [0,1,1,1,0,0,1,1] and B-C are [1,1,1,0,0,1,1,1], and the resulting FS status is [0,1,1,0,0,0,1,1]. In the route, assignable candidates are the 2^nd and 3^rd and 7^th and 8^th FSs. Like this example, a spectrum continuity constraint (i.e., same FSs should be used across links) exists, which ensures that all links in the end-to-end route use the same FSs. Spectrum assignment (SA) algorithms determine which candidates are used, as explained in the following section.

Fig. 1. Spectrum assignment example in an EON.

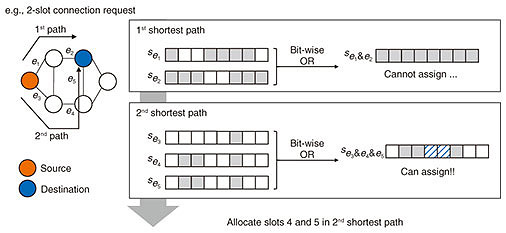
3. RSA

To give an overview of RSA, let us take an example of a well-known heuristic algorithm, the KSP and first fit (KSP-FF) algorithm. The KSP-FF algorithm solves the routing subproblem (by KSP) and SA subproblem (by FF) separately. It first determines a route then the FSs to be used. Figure 2 shows an overview of determining which route and FSs.

Fig. 2. Overview of KSP-FF algorithm.

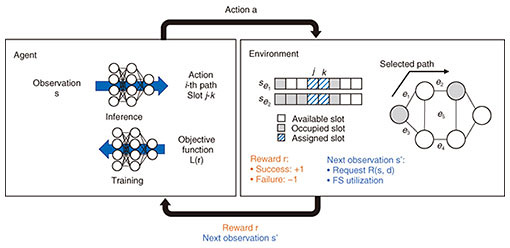
In routing, the KSP-FF algorithm first precomputes a routing table that is an ordered list of the K routes between all pair of nodes. Next, when a connection request arrives, KSPs are obtained from the routing table by using the pair of source and destination nodes. Finally, a path where assignable FSs exist is searched for in order of shorter paths. When available FSs do not exist in K routes, the connection request is rejected, which is called blocking. After routing, spectrum assignment by FF is executed; in all assignable FSs, the lowest indexed FSs are selected. This assignment procedure packs existing connections into the smallest number of FSs, leaving a larger number of available FSs.

An efficient RSA algorithm can prevent spectral fragmentation. Let us take two cases in which FSs are [1,0,0,1,0,0,1] and [0,0,0,0,1,1,1] with a 2-FS request. In the first case, there are many spectral losses, making it impossible to assign the 2-FS request. The second case allocates FSs consecutively, so there is no spectrum loss and 2-FS requests can be allocated. Therefore, preventing spectral fragmentation can allocate more requests.

4. DRL-based RSA

An overview of dynamic RSA in the format of a well-known DRL modeling is shown in Fig. 3. At each time step, the agent takes an action, and the action space is pre-defined at the formulation phase. For example, when DRL is applied to the routing subproblem that selects one of the KSPs, the action space is {1, 2, ..., K}, the action of which is mapped to the corresponding shortest path. Next, the agent receives an observation and reward from the environment. Observation is the status of the current environment which includes a request and a status of FS utilization. Reward is a value that represents how good the action is. An agent takes actions on the basis of the observation, and parameters of the agent’s action-decision function, i.e., a deep neural network (DNN) is updated to maximize the total number of rewards.

Fig. 3. Overview of DRL-based RSA.

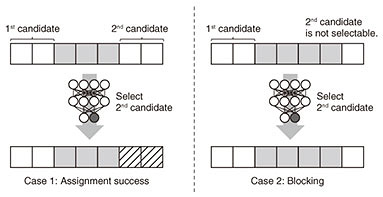
One of the key problems with DRL-based RSA is how to define the action space; assignable FSs vary time to time and depends on routing paths. Figure 4 shows an example of the FS selection from action spaces proposed in a previous study [4]. The action space is {1, 2}, the action of which is mapped to assignable candidates. In case 1, the first candidate is 1–2 FSs, and the second one is 6–7 FSs. The DNN determines which candidate should be used to accommodate as many future connection requests as possible. Unlike case 1, the problem in case 2 is that the number of assignable candidates is less than the size of the action space. In this case, for actions that are not mapped to any assignable candidates, blocking is mapped; the blocking action is selected, and its connection request is rejected. Since this definition of action cannot be used to evaluate all assignable candidates properly when the size of the action space is less than the number of assignable candidates, a trained agent would be suboptimal. Therefore, efficient DRL-based RSA algorithms need to be flexible in accordance with the changing number of assignable candidates while avoiding spectral fragmentation.

Fig. 4. Example of FS selection.

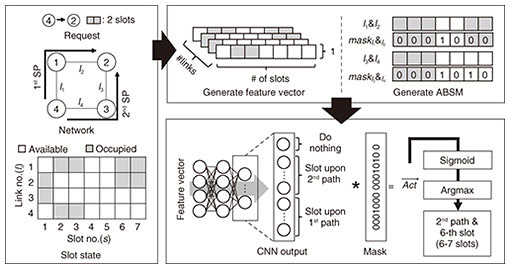
5. Mask RSA

To handle the dynamic changes in the number of assignable candidates without spectral fragmentation, our Mask RSA masks unassignable candidates to take into account assignable ones. Mask RSA is based on our past study [5].

First, we explain the definition of an action space in Mask RSA. Mask RSA implements routing by selecting one of the KSPs, and SA is executed by selecting the first index of used FSs. Thus, an action space in Mask RSA is defined as {1, 2, ..., S × K, S × K + 1}, where S and K are the numbers of FSs and paths, respectively. The option of an action is do-nothing; if assignable resources do not exist in a KSP, take the action of do-nothing, which leads to blocking. For example, when the selected action number is 120, (1) do-nothing if 120 > S × K; otherwise (2) the selected path is and the start index of used FSs is 120 mod S. This formulation makes an agent select a routing path and FSs concurrently.

Figure 5 gives an overview of Mask RSA inference. To handle dynamic changes in the number of assignable candidates, the masking approach is used. First, for each routing path, an assignable boundary slot mask is generated as a vector with its assignable position at a boundary of 1; otherwise, 0. An ABSM can prevent spectral fragmentation since it takes into account only boundaries. Next, a do-nothing mask is created; 0 when assignable candidates exist among KSPs, otherwise 1. Finally, both K ABSMs and do-nothing mask are concatenated to generate an RSA assignable mask Let softmax() and argmax() be softmax and argmax functions, respectively. The mapping function from convolutional neural network (CNN) output to an action is written as

where is a DNN output vector, and is the Hadamard product. This mask prevents both the examination of unassignable choices and spectral fragmentation.

Fig. 5. Inference of Mask RSA.

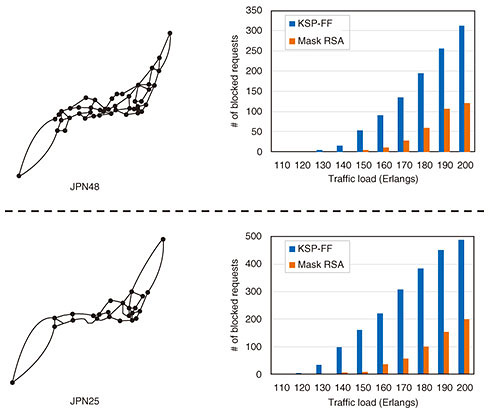
6. Demonstration

We evaluated the performance of Mask RSA by comparing it with the KSP-FF algorithm through simulations. The simulations involved a dynamic traffic scenario in which requests were generated on the basis of a Poisson process following a uniform traffic distribution. The average arrival rate and service duration for training were 10 and 12, respectively. The requested FS width was randomly selected in the range of 1 to 8. The tested networks were JPN25 (25 nodes and 43 links) and JPN48 (48 nodes and 82 links) [6]. Each FS was set to be 12.5 GHz, and each link had 320 FSs.

Figure 6 shows request blocking probabilities versus traffic loads from 110 to 200 Erlangs. In both networks, our Mask RSA outperformed the KSP-FF algorithm even when the traffic load differed from that used in training. These simulations in two topologies showed that the masking approach enabled efficient RSA regardless of the network size or traffic load used for training; accordingly, Mask RSA outperformed the KSP-FF algorithm.

Fig. 6. Simulation results.

7. Further studies

In this article, we introduced the application of DRL to dynamic optical network planning in EONs. The proposed DRL-based RSA algorithm, Mask RSA, is enhanced with domain-specific knowledge, outperforming heuristic algorithms. We plan to expand our study to more complicated networks, e.g., multi-core, multi-layer networks, and impairment-aware RSA, to enable more efficient network planning.

References

[1]	O. Gerstel, M. Jinno, A. Lord, and S. J. B. Yoo, “Elastic Optical Networking: A New Dawn for the Optical Layer?”, IEEE Commun. Mag., Vol. 50, No. 2, pp. s12–s20, Feb. 2012. doi: 10.1109/MCOM.2012.6146481
[2]	V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski, S. Petersen, C. Beattie, A. Sadik, I. Antonoglou, H. King, D. Kumaran, D. Wierstra, S. Legg, and D. Hassabis, “Human-level Control through Deep Reinforcement Learning,” Nature, 518, pp. 529–533, Feb. 2015. https://doi.org/10.1038/nature14236
[3]	X. Chen, J. Guo, Z. Zhu, R. Proietti, A. Castro, and S. J. B. Yoo, “Deep-RMSA: A Deep-reinforcement-learning Routing, Modulation and Spectrum Assignment Agent for Elastic Optical Networks,” Proc. of 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, Mar. 2018.
[4]	X. Chen, B. Li, R. Proietti, H. Lu, Z. Zhu, and S. J. B. Yoo, “DeepRMSA: A Deep Reinforcement Learning Framework for Routing, Modulation and Spectrum Assignment in Elastic Optical Networks,” J. Lightw. Technol., Vol. 37, No. 16, pp. 4155–4163, Aug. 2019.
[5]	M. Shimoda and T. Tanaka, “Deep Reinforcement Learning-based Spectrum Assignment with Multi-metric Reward Function and Assignable Boundary Slot Mask,” 2021 Opto-Electronics and Communications Conference (OECC), July 2021.
[6]	S. Arakawa, T. Sakano, Y. Tsukishima, H. Hasegawa, T. Tsuritani, Y. Hirota, and H. Tode, “Topological Characteristic of Japan Photonic Network Model,” IEICE Tech. Rep., Vol. 113, No. 91, PN2013-2, June 2013.