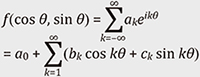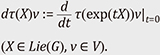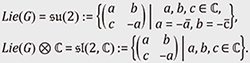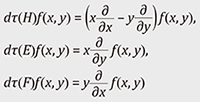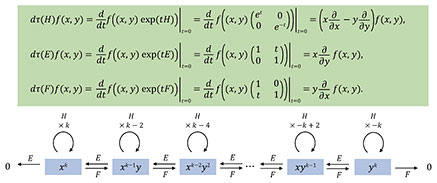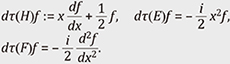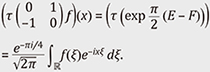|
|||||||||||||
|
|
|||||||||||||
|
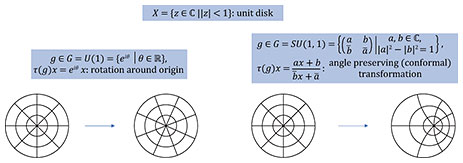
Feature Articles: Challenging the Unknown: Mathematical Research and Its Dreams Vol. 22, No. 9, pp. 53–58, Sept. 2024. https://doi.org/10.53829/ntr202409fa6 Symmetry and Representation Theory of Lie Groups and Lie AlgebrasAbstractRepresentations of Lie groups are abstractions of continuous symmetries of linear spaces. By considering their differentials (linear approximations), we obtain representations of Lie algebras. These are regarded as generalizations of the Fourier analysis and important tools not only in mathematics but also in physics. In this article, I present fundamental and important examples on representations of Lie groups and Lie algebras and present some of my latest results. Keywords: fundamental mathematics, Lie groups, Lie algebras 1. IntroductionLie groups are abstractions of continuous symmetries of spaces, and linear symmetries are abstracted by representations of Lie groups [1]. These are useful for analyzing functions on spaces with symmetries. However, Lie groups are non-linear objects, and it is not easy to treat their representations directly. To overcome this non-linearity, it is useful to consider the representations of Lie algebras by taking the differentials (linear approximations) of representations of Lie groups. These differentials preserve much information on the original representations and are easier to treat. 2. Representations of Lie groupsFirst, a Lie group is defined as a subset of the set of all n × n invertible matrices with complex entries (which is denoted as GL(n, ℂ) and called the general linear group), closed by the products, the inverses, and taking the limits*1. For example, GL(n, ℂ), GL(n, ℝ) = {n × n invertible matrices with real entries}, SL(n, ℂ) = {g ∈ GL(n, ℂ) | det(g) = 1}, O(n) = {g ∈ GL(n, ℝ) | gtg = In}, and U(n) = {g ∈ GL(n, ℂ) | gtg̅ = In} are typical examples of Lie groups (where In is the identity matrix). Next, let G be a Lie group, and X be a space such that “convergence can be defined” (i.e., a topological space). If a transformation τ(g): X → X is given for each element g ∈ G and if it satisfies the associative law and the continuity in a suitable sense, we say that G acts on X. For example, rotations of the unit disk (the disk of radius 1) around the origin are regarded as the action of the Lie group U(1). Similarly, conformal transformations of the unit disk, i.e., transformations that preserve angles of two intersecting curves, are almost regarded as the action of the Lie group SU(1, 1) (Fig. 1). These examples show that an action of G on X controls the symmetries of X.
When the space X = V on which G acts is a linear space and τ(g) is a linear map on V (i.e., it preserves additions and scalar multiplications), (τ, V) is called a representation of G. For example, if G acts on X, then G acts automatically on the space of functions on X (e.g., V = L2(X) = {ƒ: X → ℂ | ∫X|ƒ(x)|2dx < ∞}: the space of square integrable functions). This action on L2(X) is linear and becomes a representation of G. Such representation is in general infinite-dimensional and looks difficult, but in many cases, it consists of a sum of simpler representations. Therefore, to understand function spaces, it is important to understand simpler representations in detail. The most elementary example of representations of a Lie group G ⊂ GL(n, ℂ) is V := ℂn (the space of column vectors), with τ(g) defined by the product of matrices τ(g): ℂn → ℂn, τ(g)v := gv for each g ∈ G. As more non-trivial examples, for a non-negative integer k, the action of the Lie group G = U(n) on the linear space V = 𝒫k(ℂn) := {ƒ(x) = ƒ(x1, …, xn): polynomial of n variables | ƒ(tx) = tk ƒ(x) (t ∈ ℂ)} (the space of homogeneous polynomials of n variables, degree k), with τ(g) defined by the product of matrices on the variables becomes a representation. Similarly, the action of the Lie group G = O(n) on the linear space
(the space of homogeneous harmonic polynomials of n variables, degree k), with τ(g) defined similarly also becomes a representation. The representation of U(n) on 𝒫k(ℂn) and that of O(n) on ℋk(ℂn) are examples of irreducible representations. “Irreducible” means that the representation can no longer be decomposed, or there are no linear subspaces W ⊂ V satisfying τ(G)W ⊂ W other than {0} and V.
3. Irreducible decompositions of representations—Generalization of Fourier analysisOne of the most fundamental problems in representation theory is to decompose a given representation into a sum of irreducible representations. The irreducible decomposition of the function space (e.g. L2(X)) on X with an action of G is useful for understanding X. For example, G = O(n) acts on the n–1-dimensional sphere Sn–1 := {x ∈ ℝn | ∑ni=1xi2 = 1} by the usual rotations and acts on the function space L2(Sn–1) linearly. The space of the restriction of homogeneous harmonic polynomials of degree k on the sphere Sn–1 (spherical harmonic functions, denoted as ℋk(ℂn)|Sn–1 =: ℋk(Sn–1)) is then preserved by this action, and becomes a sub-representation. Namely, If ƒ(x) ∈ ℋk(Sn–1), then τ(g)ƒ(x) ∈ ℋk(Sn–1) for all g ∈ O(n). Moreover, each ƒ(x) ∈ L2(Sn–1) is expressed uniquely by the form
Hence, L2(Sn–1) is decomposed into the direct sum
Since each ℋk(Sn–1) is irreducible, this gives the irreducible decomposition. When n = 2, by the coordinate (cos θ, sin θ) of S1, we have ℋk(S1) = ℂeikθ + ℂe–ikθ = ℂ cos kθ + ℂ sin kθ = {aeikθ + a'e–ikθ = (a + a') cos kθ + i(a – a') sin kθ | a, a' ∈ ℂ}, and the above decomposition coincides with the Fourier series expansion
(bk = ak + a–k, ck = i(ak – a–k)). Similarly, the (inverse) Fourier transform
is regarded as the decomposition of the function space L2(ℝ) on the real line ℝ into the sum of one-dimensional sub-representations ℂeixξ as the representation of the additive group ℝ,
Note that this is a sum of uncountably many spaces and called the direct integral instead of the direct sum. Needless to say, the Fourier analysis is important in many fields such as signal processing, and the theory of spherical harmonics is important in the treatment of rotation-invariant systems in quantum physics. Irreducible decompositions of general representations are regarded as generalizations of these important theories. Among irreducible decompositions, the decomposition of a representation of G under its subgroup G' ⊂ G is called the branching law. For example, we consider the restriction of the representation 𝒫k(ℂn) of G = U(n) to the subgroup
Then as a representation of U(n), 𝒫k(ℂn) is irreducible but as a representation of U(n – 1), the subspaces
(m = 0, …, k) are clearly sub-representations. Therefore, we find that the irreducible decomposition (branching law) of 𝒫k(ℂn) under U(n – 1) is given by
Similarly, it is known that the irreducible decomposition of 𝒫k(ℂn) under G' = O(n) is given by
(where ‖x‖2 :=
This is then an irreducible representation of O(n – 1), and if we suitably choose
The polynomial
4. Representations of Lie algebras—Linear approximation of those of Lie groupsLie groups are generally not linear spaces, and it is not easy to treat their representations directly. To overcome this non-linearity, we consider the Lie algebras associated with the Lie groups instead. For X ∈ M(n, ℂ) (an n × n matrix with complex entries) and t ∈ ℝ, we consider the exponential function exp(tX) := Lie(G) := {X ∈ M(n, ℂ) | exp(tX) ∈ G holds for all t ∈ ℝ}. This then becomes a linear space, and [X, Y] := XY –YX ∈ Lie(G) holds for all X, Y ∈ Lie(G). Next, for a finite-dimensional representation (τ, V) of G, we define the representation (dτ, V) of the Lie algebra Lie(G) by
Then dτ(aX + bY) = adτ(X) + bdτ(Y) and dτ([X, Y]) = dτ(X)dτ(Y) – dτ(Y)dτ(X) hold for all X, Y ∈ Lie(G), a, b ∈ ℝ. This representation (dτ, V) preserves most information on the original representation (τ, V). For example, if G is connected, then the irreducibility of a finite dimensional representation (τ, V) under G is equivalent to the irreducibility of the differential representation (dτ, V) under Lie(G). Let us consider the representation of G = SU(2) := U(2) ∩ SL(2, ℂ) on V = 𝒫k(ℂ2) as an example. First, the Lie algebra Lie(G) associated with G = SU(2) and its complexification Lie(G) ⊗ ℂ are given by
We take a basis
(see Fig. 3 for the intermediate process). In particular, the actions on the basis {xk, xk–1y, xk–2y2, …, yk} of 𝒫k(ℂ2) is written as dτ(H)xk–jyj = (k – 2j)xk–jyj, dτ(E)xk–jyj = jxk–j+1yj–1, dτ(F)xk–jyj = (k – j)xk–j–1yj+1. Hence, dτ(H) has the eigenvalues {k, k – 2, k – 4, …, –k}, dτ(E) raises the eigenvalue of an eigenvector of dτ(H) by 2, and dτ(F) lowers the eigenvalue by 2. This structure is equivalent to those of the spin representations appearing in quantum physics. In fact, a general irreducible representation of SU(2) always has such a structure, especially equivalent to 𝒫k(ℂ2) for a non-negative integer k. As a higher example, we consider the representations of the Lie group U(n). Again, by looking in detail at the action of (the complexification of) the associated Lie algebra for diagonal, upper-triangular, and lower-triangular matrices, we can then show that the set of all irreducible representations of U(n) has a one-to-one correspondence with the set of n-tuples of decreasing integers {(λ1, λ2, …, λn) ∈ ℤn | λ1 ≥ λ2 ≥ ⋯ ≥ λn}. As we have seen above, representations of Lie algebras are helpful for the classification of representations of Lie groups. It is also known that the dimension of each irreducible representation of U(n) is characterized by the number of combinatoric objects called the semistandard Young tableaux.
5. Example of infinite-dimensional representationsNext, we consider an example of infinite-dimensional representations. Let us consider the Lie group G = SL(2, ℝ). Its Lie algebra is then given by
We take the basis H, E, F ∈
This does not lift to a representation of the Lie group SL(2, ℝ) but lifts to that of the double covering group
This is proved by observing the eigenfunctions of
6. Branching law of infinite-dimensional representationsIn recent research, I was interested in explicitly determining the branching laws of infinite-dimensional representations (see [2] and references therein). When we restrict a “good” representation (τ, V) of G to a subgroup G' ⊂ G, V is decomposed into a direct sum (or a direct integral) of (in general infinite number of) irreducible representations of G'. Even if we know which representation V' of G' appears abstractly in the decomposition of V, it is generally a difficult problem to determine how V' is included explicitly in V (corresponding to the determination of
References
|
|||||||||||||