Crystal Growth and Electro-optic Properties of
KTa_1−xNb_xO₃

1. Introduction

The electro-optic (EO) effect is a phenomenon in which the refractive index of a substance is modulated by an externally applied electric field. This phenomenon is used to make optical modulators where the intensity or phase of a light beam is modulated by an electric signal. Substances for which this phenomenon is significant are called electro-optic materials. The most common material is lithium niobate (LiNbO₃, LN). For LN, the EO effect is linear; that is, the refractive index change is proportional to the applied electric field. This is called the Pockels effect. Potassium tantalate niobate (KTa_1−xNb_xO₃, KTN) is another EO material that is well known because of the strength of its EO effect [1], [2]. The effect for KTN is quadratic (Kerr effect) where the refractive index change is proportional to the square of the electric field. Although the effects are different for these two materials, it is possible to compare their figures of merit by introducing a bias electric field. We can expect the EO effect to be more than ten times larger for KTN than for LN. To date, however, there have not been any commercial products utilizing KTN, while LN is already used in various products such as 40-Gbit/s light modulators for fiber-optic telecommunication in addition to surface acoustic wave filters for mobile phones. One important reason of this is that KTN crystal has been difficult to grow compared with LN. In 2003, our laboratories succeeded in growing sizable crystals of optical quality with volumes of over 30 cm³ (e.g., 40 mm × 40 mm × 20 mm) [3]. We recently improved the growth technique to achieve a high degree of reproducibility. Moreover, we additionally found that significant light beam deflection occurs in KTN single crystals [4], [5]. Promising beam deflection devices are expected to be developed by utilizing this new phenomenon.

In this paper, we introduce KTN crystal and its EO properties. Then, we review a growth technique called the top seeded solution growth method used for KTN single crystals [6]. We also present some examples of the EO properties of our crystals to show the high performance of KTN.

2. Potassium tantalate niobate

KTN is the mixture or solid solution of potassium niobate and potassium tantalate. Potassium niobate (KNbO₃, KN) is also a well-known oxide crystal that is commonly used for optical second harmonic generation via its optical nonlinear effect. It is one of the perovskite-type materials whose general formula is ABO₃. The crystallographic structure of perovskite is shown in Fig. 1. Cations of A are at the corners, cations of B go into the body center, and oxygen anions are at the face centers. The unit is drawn in a cubic shape in Fig. 1. In fact, it is cubic for KN crystals at high temperatures over 435°C. However, a KN crystal undergoes three phase transitions when cooling from such high temperatures, and its crystallographic structure changes. At the first transition, the cubic structure changes to a tetragonal structure. Next, it becomes orthorhombic, which is the phase at around room temperature. It then becomes rhombohedral at low temperatures. KN is regarded as a ferroelectric substance. It thus has spontaneous polarization with zero electric field. In the cubic phase, however, the spontaneous polarization vanishes and the crystal is paraelectric. Potassium tantalate (KTaO₃, KT) is also a perovskite oxide. However, it does not undergo any phase transitions as the temperature changes but remains cubic. Therefore, the mixture KTN has three phase transitions like KN, but the transition temperatures change with the composition. All the transition temperatures rise as the KN fraction increases, as shown in Fig. 2 [1], [7].

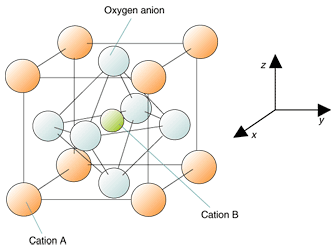
Fig. 1. Crystallographic structure of ABO₃ perovskite.

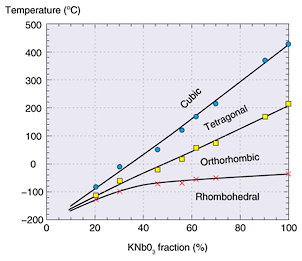
Fig. 2. Concentration dependence of the three transition temperatures for KTN.

KTN has a strong Kerr effect in the cubic phase, so it is usually used in the cubic phase. Suppose that a light beam propagates along the x direction in Fig. 1, the vibrating electric field of the light is parallel to the y direction, and a constant external electric field is applied also along the y direction. The resulting change in the refractive index caused by the external electric field is expressed as

where n₀ is the original refractive index, E is the external field, and s₁₁ is one of the Kerr coefficients. This s₁₁ is given by [8]

where ε, ε₀, and ε_r are the KTN permittivity, the vacuum permittivity, and the relative dielectric constant, respectively, and g₁₁ is a function of the wavelength of the light but depends on neither ε_r nor the temperature. Because ε_r is much larger than 1 for KTN crystals, we can regard s₁₁ as being proportional to ε_r². According to the Curie-Weiss law, ε_r becomes significantly large at temperatures just above the phase transition temperature (the upper curve in Fig. 2. Hereinafter, the phase transition means the transition between the cubic and tetragonal phases and T_c means the temperature where this transition occurs). Therefore, we can obtain a huge Kerr coefficient s₁₁ at room temperature by choosing the composition (KN fraction) so that T_c is around room temperature. We discuss the values of ε_r and s₁₁ in section 4.

3. Crystal growth

It is essential to grow sizable single crystals with good optical homogeneity for EO oxide materials such as LN and KTN. KTN single crystals are grown by a method called top seeded solution growth (TSSG) [6], which is similar to the Czochralski method used for LN or silicon crystals. The growth apparatus for KTN single crystals is shown in Fig. 3. The furnace uses resistance heating elements. The mixed ingredients of the crystals are melted in the platinum crucible at temperatures such as 1200°C. We dip a seed crystal into the molten ingredients, slowly cool it, and thereby grow a crystal gradually from the seed. The seed crystal is attached to a rod that is simultaneously rotated and lifted by a mechanism located outside the furnace. This apparatus is almost the same as those used for Czochralski growth.

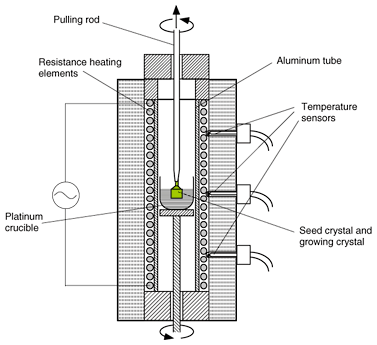
Fig. 3. TSSG apparatus for KTN single crystal growth.

However, KTN single crystals have been much more difficult to grow than conventional materials. This is mainly due to the fact that the grown crystals have different compositions from the molten ingredients. The phase diagram of the KT-KN system at elevated temperatures is shown in Fig. 4 to explain this situation [9]. The diagram shows two temperature curves as functions of composition, T_l (x) and T_s (x). T_l (x) is called the liquidus and T_s (x) the solidus. Above the liquidus, the substance is completely liquid. Below the solidus, the substance is solid. When we intend to grow a crystal from material with composition X₀, we melt the material by heating it through the liquidus temperature T₀ = T_l (X₀). We then cool it to T_l (X₀) and below. Here, the material is no longer completely liquid and solidification occurs. The composition of the solid (or crystal) is x₀, which gives the same temperature T₀ on the solidus T_s (x₀). The KN fraction of the growing crystal is less than that of the liquid. Thus, niobium left over from the solidification is gradually concentrated in the liquid, especially near the growth interface. This concentration causes instability of the growth interface. Irregular growth is likely to occur in such a situation if the growth is too fast. Moreover, it is common to start the growth with a melt that contains additional potassium oxide with KTN ingredients because potassium oxide easily evaporates from the hot melt. Therefore, excess potassium also tends to be concentrated as the growth proceeds. As a result, single crystal growth of KTN is more difficult than that of conventional materials such as LN. The additional potassium oxide acts as a kind of solvent, and the melt is a solution. Therefore, the growth technique for KTN crystals is called the top seeded solution growth method.

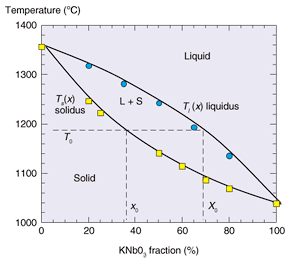
Fig. 4. Phase diagram at elevated temperatures to show the thermal equilibrium between the liquid and solid during the crystal growth.

The most noticeable defects in KTN crystals are inclusions containing excess potassium. They strongly scatter light beams and cause inhomogeneous variations in the refractive index around them. The main reason for the formation of the inclusions is excessive supercooling of the solution or excessively fast growth. We succeeded in suppressing the occurrence of inclusions by carefully controlling the furnace temperature and the growth speed [3]. We can now reproducibly grow sizable KTN crystals (> 30 cm³) without inclusions. A photograph of one of our crystals is shown in Fig. 5. The stump of the seed crystal can be seen on the center of the top face. Neither inclusions nor other irregular growths were observed. Sharp growth facets are often observed for crystals grown in furnaces with resistance heaters because of the gentle temperature gradient around the crucible. KTN crystals have a strong tendency to show crystallographic (001) faces [6]. Thus, it is possible to see through the mirror surface of the crystal in Fig. 5 even though we did not cut or polish it.

Fig. 5. Example of as-grown KTN single crystal.

4. Electro-optic properties

As described above, the relative dielectric constant of paraelectric KTN ε_r obeys the Curie-Weiss law:

Here, T_cp is the paraelectric Curie temperature. Thus, ε_r increases drastically as the temperature approaches T_cp. To obtain ε_r as a function of temperature, we cut a 6 mm × 5 mm × 1 mm chip from a grown single-crystal boule, polished its surfaces, formed a pair of platinum electrodes by evaporation, and measured its capacitance on a temperature-controlled aluminum block. The size of the electrodes was 5 mm × 1 mm and the gap between them was 1 mm. The applied voltage was 10 V_p-p AC with a frequency of 20 Hz. An example of the relative dielectric constant as a function of temperature is shown in Fig. 6(a). For this chip, the phase transition occurred at around 35°C. Above this phase transition temperature T_c, it was in the cubic phase. Below T_c, it was in the tetragonal phase. For this composition (or this T_c), it is known that the phase transition is of the first order and that T_cp is slightly lower than T_c. The reciprocal of the relative dielectric constant as a function of temperature is shown in Fig. 6(b). The 1/ε_r apparently obeyed the Curie-Weiss law (Eq. 3). It can also be seen in this figure that T_cp was slightly lower than T_c. When a KTN single crystal in the cubic phase is cooled, the temperature reaches T_c and the crystal enters the tetragonal phase before the temperature reaches T_cp. Thus, the relative dielectric constant falls to the low value of the tetragonal phase before going up to infinity. The relative dielectric constant is limited by this characteristic. In addition, it is limited in practice by T_c ambiguity as a result of the lack of compositional uniformity. However, we are now able to reproducibly obtain a dielectric constant higher than 20,000. This high dielectric constant enables a very large Kerr effect to be obtained according to Eq. (2). The temperature dependence of the Kerr coefficient s₁₁ is shown in Fig. 7. The coefficient was measured using a Mach-Zehnder interferometer. We placed one of the chips described above on one of the two arms of the interferometer, applied a low-frequency AC voltage to the chip, monitored the output optical power, and determined the half-wave voltage V_π (V_π is discussed later in this section). The maximum value was 2.24 × 10⁻¹⁴ m²/V², which is, to our knowledge, about 8 times larger than that previously reported for KTN [2]. We ascribe this to the compositional uniformity. The Pockels coefficient for the conventional material LN is said to be about 30 pm/V. Direct comparison between the Pockels effect for LN and the Kerr effect for KTN is not possible. However, by applying a DC bias voltage together with the control signal, we can use a KTN chip in a similar manner to an LN chip. For a DC bias electric field E₀, which is much larger than the signal electric field E_s, Eq. (1) is rewritten as

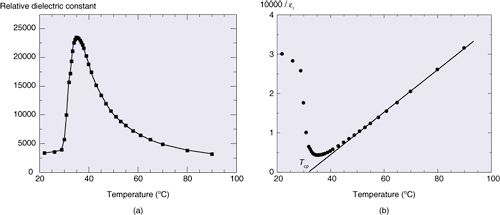
Fig. 6. Temperature dependence of (a) relative dielectric constant ε_r and (b) 1/ε_r.

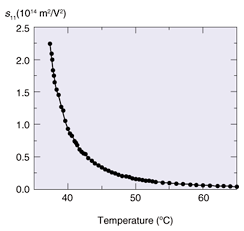
Fig. 7. Temperature dependence of Kerr coefficient s11.

Here, the first term has no relation to the signal. The second term is the same as the refractive index modulation for the Pockels effect. The pseudo Pockels coefficient corresponds to 2_s11E₀. When we apply a voltage of 100 V between a pair of electrodes whose gap is 1 mm, the Pockels coefficient becomes 2240 pm/V. This is 70 times larger than the value for the effect in LN.

Our beam deflection devices utilize this huge electro-optic effect and the large dielectric constant. Details are explained in another paper in this issue [10]. Here, we discuss the merit in applications to light intensity modulators. The simplest modulator can be fabricated by placing an EO material with electrodes between a pair of crossed polarizers. The half-wave voltage V_π, which is the voltage difference required to change the transmittance from 0% to 100%, is expressed by

where λ₀, r, d, and l are the wavelength of the light to be modulated, the effective Pockels coefficient, the electrode gap, and the length of the light path in the EO material. Thus, when the effective Pockels coefficient is 70 times larger, we can reduce V_π to 1/70. If we permit the same V_π, it is possible to reduce l, that is to shrink the device size. Accordingly, we can expect either a drastic reduction in the load on the voltage controller or significant miniaturization of the modulators.

5. Conclusion

We introduced the growth of KTN single crystals and their electro-optic properties. By carefully controlling the temperature in the TSSG method, we can now reproducibly grow crystals with sizes of more than 30 cm³ with no visible defects. KTN is known for its large Kerr effect. Because of compositional homogeneity, the Kerr coefficient s₁₁ of our crystals exceeded 2.2 × 10⁻¹⁴ m²/V², which is about 8 times higher than the previously reported value. It also corresponds to a value 70 times larger than the Pockels coefficient for LN when the bias field is 100 V/mm. Great improvements are expected if the EO material in conventional light modulators is replaced with KTN single crystals.

References

	Tadayuki Imai Senior Research Engineer, Advanced Opto-electronics Laboratory, NTT Photonics Laboratories. He received the B.E. degree in electrical engineering from Doshisha University, Kyoto, in 1990. He then received the M.E. and Ph.D. degrees in electrical engineering from Osaka University, Osaka, in 1992 and 2000, respectively. He joined NTT Interdisciplinary Research Laboratories in 1992. He has been engaged in the development of holographic memories and electro-optic devices and crystal growth of inorganic materials. He is a member of the Japan Society of Applied Physics (JSAP) and the Japanese Association for Crystal Growth.
	Masahiro Sasaura Senior Research Engineer, Advanced Opto-electronics Laboratory, NTT Photonics Laboratories. He received the B.E. and M.E. degrees in applied physics and crystalline materials science from Nagoya University, Aichi, in 1985 and 1987, respectively. He joined NTT Atsugi Electrical Communication Laboratories in 1987. Since then, he has been engaged in the development of crystal growth methods. The grown crystals include Si, GaAs, high-Tc superconductor, gallates (oxides) for high-Tc superconductor substrates, and niobates (oxides) for electro-optic devices.
	Koichiro Nakamura Research Specialist, Advanced Opto-electronics Laboratory, NTT Photonics Laboratories. He received the B.S., M.S., and Ph.D. degrees in electronic engineering from Tohoku University, Miyagi, in 1994, 1995, and 1998, respectively. Prior to those degrees, he received the A.D. in radio communication from Kumamoto National College of Technology, Kumamoto, in 1991. At Tohoku University, he was engaged in research on the oscillation mechanisms of frequency-shifted feedback lasers and their applications in optical measurement. In 1998, he joined the Research Institute of Electrical Communication, Tohoku University, where he was a Research Associate and engaged in research on nonlinear optical frequency conversion using periodically poled ferroelectric materials. From 2000 to 2001, he was a visiting researcher at Ginzton Laboratory, Stanford University, USA. In 2001, he joined Lightbit Corporation, Mountain View, California, USA, where he was an Integrated Optics Scientist and engaged in R&D of ultrafast optical communication devices based on the cascaded second-order optical nonlinearity in periodically poled ferroelectric materials. He was a researcher (non-full-time) in the RIKEN Photodynamics Research Center from 2001 to 2002. In 2004, he joined NTT Photonics Laboratories. Since then, he has been engaged in research on the material properties of KTN crystal and development of optical devices based on KTN crystal. He was a fellow of the Optoelectronics Gakujikai from 1995 to 1998 and a research fellow of the Japan Society for the Promotion of Science from 1997 to 1998. He has been a committee member of the MOT (management of technology) education program at Nara Institute of Science and Technology since 2005. He received the Ericsson Young Scientist Award in 1998, the JSAP Award for Research Paper Presentation in 1998, the Niwa Yasujiro Memorial Award in 1998, the IEICE (Institute of Electronic, Information and Communication Engineers of Japan) Award for Research Paper Presentation in 2000, and the IEICE Best Paper Award in 2003. He is a member of JSAP, IEICE, and the Optical Society of America.
	Kazuo Fujiura Senior Research Engineer, Supervisor, Advanced Opto-electronics Laboratory, NTT Photonics Laboratories. He received the B.S. and M.S. degrees in applied chemistry from Kyushu University, Fukuoka, in 1983 and 1985, respectively. Since joining NTT Laboratories in 1985, he has been engaged in research on fluoride glass fiber fabrication technology. In 1993, he received the Ph.D. degree from Kyushu University for his work entitled “Studies on Synthesis and Properties of ZrF4-Based Fluoride Glasses by Chemical Vapor Deposition.” From 1996 to 1997, he was a visiting scholar at Stanford University. Since 2001, he has been engaged in research on KTN optical devices. He received the 49th Award of the Ceramic Society of Japan and the Joint Ceramics Award of the Japanese and Australian Ceramics Societies. He is a member of IEICE, JSAP, the Ceramics Society of Japan, the Chemical Society of Japan, and the Materials Research Society.

↑ TOP