You need Adobe Reader 7.0 or later in order to read PDF files on this site.
If Adobe Reader is not installed on your computer, click the button below and go to the download site.

Selected Papers:	Growth Technologies and Device Applications of Electro-optic Crystal KTa_1−xNb_xO₃

System for Measuring the Phase Transition Temperature of KTa_1−xNb_xO₃ Using Scanning Nonlinear Dielectric Microscopy

Takashi Sakamoto^†, Koichiro Nakamura, and Kazuo Fujiura

Abstract

We have developed a system for measuring the paraelectric-to-ferroelectric phase transition temperatureT_C using scanning nonlinear dielectric microscopy (SNDM). We developed a probe for samples with a huge dielectric constant and demonstrated that theT_C of potassium tantalate niobate (KTa_1−xNb_xO₃, KTN) crystal can be measured locally using SNDM with this probe. The T_C measurement precision (standard deviation) is 0.09°C. This corresponds to a composition (Nb concentration x) resolution of 1.4 × 10⁻⁴, which is difficult to achieve with other element analyzers. Moreover, by measuring T_C while changing the position, we demonstrated that we can measure the spatial distribution of the T_C of the KTN crystal. To reduce the time required for the operator to measure the T_C distribution of the KTN crystal, we developed software for fully automated operation.

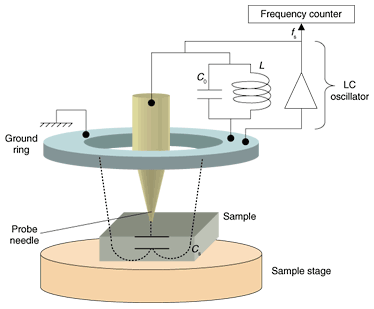
†	NTT Photonics Laboratories Atsugi-shi, 243-0198 Japan Email: skmt@aecl.ntt.co.jp

1. Introduction

Potassium tantalate niobate (KTa_1−xNb_xO₃, KTN) is a ferroelectric material and its dielectric constant and quadratic electro-optic (EO) constant (Kerr constant) are maximum around the paraelectric-to-ferroelectric phase transition temperature (T_C) [1]. These values are huge, so KTN is expected to reduce both the volume and driving voltage of EO devices, such as optical beam deflectors [2] and modulators [3]. In KTN, T_C can be adjusted by changing the composition, i.e., the Ta/Nb ratio [1]. T_C increases linearly with the amount of Nb (x) [4]. However, if there is a spatial change in the Ta/Nb ratio in a crystal, which may be induced by changes in the growth condition during crystal growth, T_C changes spatially, and the dielectric constant ε and the Kerr constant s change spatially at a given temperature. If a crystal’s spatial distributions of ε and s are large (i.e., the crystal is highly inhomogeneous), it is difficult to guarantee the characteristics of an EO device manufactured from that crystal. Therefore, to guarantee the characteristics of a KTN device, it is necessary to evaluate the uniformity of a crystal’s T_C before the device is manufactured. However, if TC has to be estimated with a precision of 0.1°C, the composition should be estimated with a precision of 1.5 × 10⁻⁴ [4]. This is difficult to achieve with conventional element analyzers, such as an electron probe microanalyzer (EPMA).

In this paper, we describe the system for measuring the T_C of KTN that we developed. First, we review scanning nonlinear dielectric microscopy (SNDM) and describe the probe we developed for samples having a huge dielectric constant. Then, we describe our demonstration that the T_C of KTN crystal can be measured locally using SNDM with our probe. Experimental results for T_C measurement precision and the spatial distribution of the T_C of the KTN crystal are also presented. Finally, we introduce the software developed to reduce the time taken for the operator to measure the T_C distribution of a KTN crystal.

2. Scanning nonlinear dielectric microscopy (SNDM)

2.1 Principle of SNDM

Scanning nonlinear dielectric microscopy (SNDM) has been developed to measure the local dielectric constant under a probe needle with high spatial resolution [5], [6]. Moreover, non-destructive measurement is possible, so a crystal that has been evaluated using SNDM can be used for manufacturing devices. A schematic diagram of SNDM is shown in Fig. 1. SNDM uses an LC (inductance and capacitance) oscillator with a probe needle. 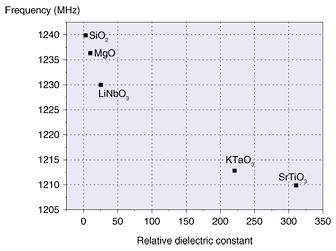When the probe needle is far away from the sample, the resonant frequency f₀ is , where L and C₀ are the oscillator’s inductance and capacitance (including stray capacitance), respectively. When the tip of the probe needle makes contact with the sample, the resonant frequency f_S is , where C_S is the capacitance of the sample under the probe needle. As the dielectric constant of the sample under the probe needle increases, C_S becomes larger and f_S becomes lower.

Fig. 1. Schematic diagram of SNDM.

To check this, we measured the resonant frequency of several dielectric materials. The relationship between f_S and the dielectric constant at room temperature is shown in Fig. 2. This figure clearly indicates that the larger the dielectric constant, the lower f_S. Accordingly, when f_S is measured as a function of temperature, the local T_C can be obtained as the temperature that gives the lowest f_S. Moreover, the spatial distribution of T_C can be measured by changing the point touched by the probe.

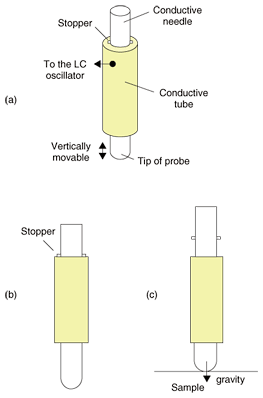
Fig. 2. Resonant frequency f_S versus relative dielectric constant.

2.2 Probe for keeping contact force constant

In crystals with a huge dielectric constant, such as KTN, f_S depends strongly on the contact force that the probe needle exerts on the sample. The reason for this is as follows: when the probe needle is in point contact with a sample having a huge dielectric constant, the electric field is concentrated in a very small area just under the tip of the probe needle [7], and f_S depends on the capacitance of that very small area. When the contact force is stronger, the contact area is larger due to deformation, and f_S depends on the capacitance of the larger area and is lower; namely, f_S depends on both the dielectric constant and the contact force.

In the work described here, we developed a probe that keeps the contact force constant during the measurement of T_C. A schematic diagram of the probe is shown in Fig. 3(a). The probe consists of a conductive tube and a conductive needle that can move up and down in the tube, which has a stopper to prevent the needle from falling out. When the tip of the probe is not in contact with a sample, the needle is held by the stopper, as shown in Fig. 3(b). On the other hand, when the tip is in contact, the sample pushes the needle upwards, as shown in Fig. 3(c). With this design, the contact force is equal to the force of gravity acting on the needle and can be kept constant.

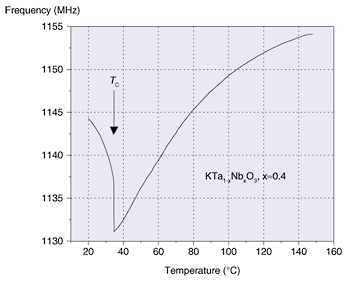
Fig. 3. Probe for keeping contact force constant. (a) Configuration, (b) no contact with sample, and (c) in contact with sample.

3. Experimental results

3.1 Measurement of T_C of KTN

The resonant frequency f_S is plotted as a function of temperature T in Fig. 4 when the probe needle (Au-coated, tip radius: 500 µm) came into contact with a KTN single crystal (6 × 5 × 0.5 mm³, x ≈ 0.4). We estimated T_C to be about 35°C because domains appeared or disappeared at this temperature. The f_S was about 1214 MHz when the probe needle was kept far away from the sample; namely, C_S = 0. We used a Peltier device and a controller to sweep the temperature and we collected data during the cooling phase. The sweep rate was not constant, but the average rate was about 0.3°C/s. As shown in the figure, f_S was minimum at around 35°C. This indicates that SNDM can measure the T_C of KTN.

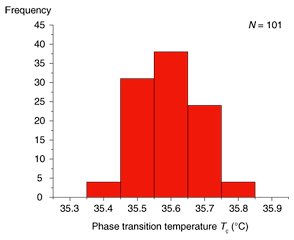
Fig. 4. Resonant frequency f_S as a function of temperature when the probe made contact with KTN crystal.

3.2 T_C measurement precision

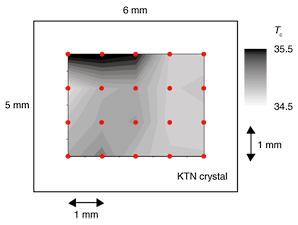
We evaluated the precision of this method. We performed the T_C measurement N times, where N = 101. A histogram of T_C is shown in Fig. 5. Here, for T_C, we used the temperature at which df_S/dT was the smallest because it changes drastically around T_C, as shown in Fig. 4. This large change is induced by an abrupt change in the dielectric constant. The mean value of T_C, _C, was 35.6°C, and the standard deviation was 0.09°C. If we use the standard deviation as the precision, then the precision of this method is 0.09°C, which corresponds to a composition resolution of 1.4 × 10⁻⁴, using the empirical equation T_C = 676x + 32 measured in kelvin, where x is the amount of Nb [4]. This precision for the composition is difficult to achieve with other element analyzers, such as an EPMA.

Fig. 5. Histogram of 101 measurements of T_C.

3.3 Spatial distribution of T_C

Next, we evaluated the T_C distribution of the crystal. We measured T_C at 20 (= 5 × 4) points with a spacing of 1 mm. The distribution is shown in Fig. 6. For this crystal, T_C is higher in the top left of the figure. The maximum and minimum T_C values were 35.37 and 34.7°C, respectively. Here, T_C = 35.37°C corresponds to x = 0.4091 and 34.7°C to x = 0.4081, where x is the amount of Nb. Therefore, the variation in T_C in this crystal was 0.67°C, which corresponds to a variation in composition of about 0.001 using the above empirical equation [4].

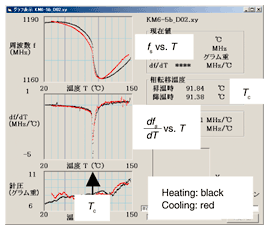
Fig. 6. Spatial distribution of T_C of KTN crystal.

4. Measurement system

To reduce the time required for the operator to evaluate the T_C distribution of the KTN crystal, we automated the measurement and data processing. A window of the software we developed is shown in Fig. 7. After the measurement condition (measurement spacing and number of points etc.) has been assigned and the sample has been set, the measurement is finished in a fully automated manner. Moreover, to eliminate manual data processing after the measurement, the software detects T_C by a differential calculation, as discussed in section 3.2 and records it.

Fig. 7. Window of software developed for fully automated measurement.

5. Conclusion

We described our system for measuring the phase transition temperature T_C of KTN using SNDM and a newly developed probe designed to keep the contact force constant during the temperature sweep. The precision (standard deviation) is 0.09°C, which corresponds to a composition resolution of 1.4 × 10⁻⁴. By measuring T_C while changing the position, we demonstrated that we could measure the T_C distribution of the KTN crystal. We also developed software capable of measuring the T_C distribution of the KTN crystal in a fully automated manner. This measurement system will enable the uniformity of KTN crystals to be evaluated, so it will be possible to guarantee the characteristics of KTN devices made from KTN crystals.

6. Acknowledgments

We thank Professor Yasuo Cho of Tohoku University for fruitful discussions about SNDM.

References

[1]	S. Triebwasser, “Study of Ferroelectric Transitions of Solid-Solution Single Crystals of KNbO₃-KTaO₃,” Phys. Rev., Vol. 114, No. 1, pp. 63–70, 1959.
[2]	K. Nakamura, J. Miyazu, M. Sasaura, and K. Fujiura, “Wide-angle, low-voltage electro-optic beam deflection based on space-charge-controlled mode of electrical conduction in KTa_1−xNb_xO₃,” Appl. Phys. Lett., Vol. 89, No. 13, 131115-1–131115-3, 2006.
[3]	S. Toyoda, K. Fujiura, M. Sasaura, K. Enbutsu, A. Tate, M. Shimokozono, H. Fushimi, T. Imai, K. Manabe, T. Matsuura, T. Kurihara, S. C. J. Lee, and H. de Waardt, “KTN-crystal-waveguide-based electro-optic phase modulator with high performance index,” Electron. Lett., Vol. 40, No. 13, pp. 830–831, 2004.
[4]	D. Rytz, A. Châtelain, and U. T. Höchli, “Elastic properties in quantum ferroelectric KTa_1−xNb_xO₃,” Phys. Rev. B, Vol. 27, No. 11, pp. 6830–6840, 1983.
[5]	K. Ohara and Y. Cho, “Quantitative Measurement of Linear Dielectric Constant Using Scanning Nonlinear Dielectric Microscopy with Electro-Conductive Cantilever,” Jpn. J. Appl. Phys., Vol. 41, No. 7B, pp. 4961–4964, 2002.
[6]	Y. Cho, S. Kazuta, K. Ohara, and H. Odagawa, “Quantitative Measurement of Linear and Nonlinear Dielectric Characteristics Using Scanning Nonlinear Dielectric Microscopy,” Jpn. J. Appl. Phys., Vol. 39, No. 5B, pp. 3086–3089, 2000.
[7]	T. Sakamoto, K. Nakamura, K. Fujiura, and Y. Cho, “Spatial distribution of phase transition temperature of KTa_1−xNb_xO₃ measured using scanning nonlinear dielectric microscopy,” Appl. Phys. Lett., Vol. 90, 222908-1–222908-3, 2007.

	Takashi Sakamoto Research Engineer, Advanced Opto-electronics Laboratory, NTT Photonics Laboratories. He received the Bachelor of Liberal Arts and M.S. (multidisciplinary sciences) degrees from the University of Tokyo, Tokyo, in 1994 and 1996, respectively. In 1996, he joined NTT Opto-electronics (now Photonics) Laboratories, where he engaged in research on optical interconnections and optical packet switching. Since 2004, he has been working on scanning nonlinear dielectric microscopy (SNDM) and device applications of KTN crystals. He is an associate member of IEEE.
	Koichiro Nakamura Research Specialist, Advanced Opto-electronics Laboratory, NTT Photonics Laboratories. He received the B.S., M.S., and Ph.D. degrees in electronic engineering from Tohoku University, Miyagi, in 1994, 1995, and 1998, respectively. Prior to those degrees, he received the A.D. in radio communication from Kumamoto National College of Technology, Kumamoto, in 1991. At Tohoku University, he was engaged in research on the oscillation mechanisms of frequency-shifted feedback lasers and their applications in optical measurement. In 1998, he joined the Research Institute of Electrical Communication, Tohoku University, where he was a Research Associate and engaged in research on nonlinear optical frequency conversion using periodically poled ferroelectric materials. From 2000 to 2001, he was a visiting researcher at Ginzton Laboratory, Stanford University, USA. In 2001, he joined Lightbit Corporation, Mountain View, California, USA, where he was an Integrated Optics Scientist and engaged in R&D of ultrafast optical communication devices based on the cascaded second-order optical nonlinearity in periodically poled ferroelectric materials. He was a researcher (non-full-time) in the RIKEN Photodynamics Research Center from 2001 to 2002. In 2004, he joined NTT Photonics Laboratories. Since then, he has been engaged in research on the material properties of KTN crystal and development of optical devices based on KTN crystal. He was a fellow of the Optoelectronics Gakujikai from 1995 to 1998 and a research fellow of the Japan Society for the Promotion of Science from 1997 to 1998. He has been a committee member of the MOT (management of technology) education program at Nara Institute of Science and Technology since 2005. He received the Ericsson Young Scientist Award in 1998, the JSAP (Japan Society of Applied Physics) Award for Research Paper Presentation in 1998, the Niwa Yasujiro Memorial Award in 1998, the IEICE (Institute of Electronic, Information and Communication Engineers of Japan) Award for Research Paper Presentation in 2000, and the IEICE Best Paper Award in 2003. He is a member of IEICE, the Japan Society of Applied Physics (JSAP) and the Optical Society of America.
	Kazuo Fujiura Senior Research Engineer, Supervisor, Advanced Opto-electronics Laboratory, NTT Photonics Laboratories. He received the B.S. and M.S. degrees in applied chemistry from Kyushu University, Fukuoka, in 1983 and 1985, respectively. Since joining NTT Laboratories in 1985, he has been engaged in research on fluoride glass fiber fabrication technology. In 1993, he received the Ph.D. degree from Kyushu University for his work entitled “Studies on Synthesis and Properties of ZrF₄-Based Fluoride Glasses by Chemical Vapor Deposition.” From 1996 to 1997, he was a visiting scholar at Stanford University. Since 2001, he has been engaged in research on KTN optical devices. He received the 49th Award of the Ceramic Society of Japan and the Joint Ceramics Award of the Japanese and Australian Ceramics Societies. He is a member of IEICE, JSAP, the Ceramics Society of Japan, the Chemical Society of Japan, and the Materials Research Society.