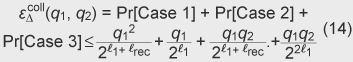Message Recovery Signature Schemes from Sigma-protocols

2.1 Notation

We consider uniform probabilistic algorithms (i.e., Turing machines) that take as input (the unary encoding of) a security parameter λ ∈ and possibly other inputs and run in deterministic polynomial time in λ. We thus always implicitly require the size of the input to be bounded by some polynomial in λ. Adversarial behavior is modeled by non-uniform polynomial-time probabilistic algorithms, i.e., by algorithms that together with the security parameter λ also get a polynomial-sized auxiliary input aux_λ. To simplify the notation, we usually let the dependency on λ (and on aux_λ) remain implicit. By A(x), we denote the output distribution of a probabilistic algorithm A with input x and uniformly chosen randomness. By y ← A(x), we mean that algorithm A is executed on input x and the output is assigned to y. We may also denote it as y ← A(x; r) when the randomness r is to be explicitly noted. For any algorithm A, the output domain of A is denoted by Dom(A). Similarly, for any finite set S, we use the notation y ← S to denote that y is sampled uniformly from S, and y ← x means that the value x is assigned to y. By BitLen(S), we denote the number of bits used to present the largest element in S.

|X| is used in different ways. If X is a set, |X| denotes the cardinality of X. If X is a distribution or an algorithm, |X| denotes the number of elements in X with nonzero probability. If X is a variable whose actual value is taken from some range, |X| denotes the number of bits needed to present the maximum value in the range. (Hence, |X| does not necessarily equal [log₂ X] for the actual value assigned to X.) Finally, if X is a string, |X| is the number of bits needed to present the string.

We use X := Y to define a new variable X with Y. For any two strings a and b, a||b denotes a string that concatenates a and b in order. By a||b ← c, we denote that string c is separated into two parts and assigned to a and b. The manner of separation depends on the context but may not be explicitly given when it is clear from the context.

P[y = A(x)] denotes the probability (taken over a uniformly distributed random tape) that A outputs y on input x, and we write P[x ← B : A(x) = y] for the (average) probability that A outputs y on input x when x is output by B: P[x ← B: A(x) = y] = Σ_x P[y = A(x)]P[x = B]. We also use natural self-explanatory extensions of this notation.

An oracle algorithm A is an algorithm in the above sense connected to an oracle in that it can write on its own tape an input for the oracle and tell the oracle to execute it. Then, in a single step, the oracle processes this input in the prescribed way and writes its output on the tape. We write A^O when we consider A to be connected to the particular oracle O.

As is common practice, a value v(λ)∈R, which depends on the security parameter λ, is treated as negliible, denoted by v(λ) ≤ negl(λ) or v ≤ negl, if ∀c > 0∃λ′∈∀λ ≥ λ′: v(λ) < 1/ λ^c.

2.2 Sigma-protocol

Let L⊂{0, 1}^* be a language and R_L be a binary relation associated with L. Let W_L(x) for x∈L denote a set of witnesses for x, i.e., W_L(x) = {|R_L (x, w) = 1}. Let L be an instance generator for L that takes security parameter λ and chooses an instance x∈L and a witness w∈W_L(x) with restriction |x| = λ. A sigma-protocol for language L is an honest verifier zero-knowledge proof system that consists of (probabilistic) polynomial-time algorithms (A, C, Z, V, E, M). These algorithms work as follows.

For (x, w) ← L(λ), the verifier is given x and the prover is given (x, w). The prover first sends the first message a ← A(x; t) to the verifier and the verifier challenges the prover by returning c ← C(x). The prover answers the challenge by sending z ← Z(w, t, c) to the verifier. The verifier accepts if a = V(x, c, z). (More generally, V can be an algorithm that takes (a, x, c, z) as input and returns 1 or 0 to report acceptance and rejection. Note, however, that it is essential for our purpose that a can be computed from (x, c, z) in polynomial time.) We assume perfect correctness, where the verifier accepts with probability 1 when both the prover and verifier are honest.

A sigma-protocol features special soundness. That is, there exists a deterministic polynomial-time algorithm E, called an extractor, that takes two acceptable transcripts with the same first message and different challenges, say (x, a, c, z) and (x, a, c′, z′) such that x∈L, c ≠ c′, V(x, c, z) = V(x, c′, z′) = a as input and outputs a witness w for x with probability 1 in polynomial time.

A sigma-protocol is honest verifier zero-knowlede. Namely, we assume that there exists a polynomial-time algorithm called a simulator, denoted by M, that takes x∈L and c ← C(x) as input and outputs (a, z) such that the distribution of simulated (a, c, z) is identical to the distribution of the real transcript generated by the honest prover and verifier.

A note on relaxation. We can allow a small error probability in the correctness but the resulting signature scheme inherits the error probability in its correctness. Similarly, E can be a probabilistic algorithm with negligible error probability. Also, the quality of zero-knowledge simulator M can be relaxed to statistical or computational rather than perfect. These relaxations affect the unforgeability of the resulting signature scheme.

2.3 Security model of message recovery signature scheme

To define the security precisely, we first must present a syntactical definition of message recovery signature schemes. The one shown below is a very standard definition, which can be seamlessly turned into the definition of ordinary signature schemes with appendix by letting the non-recoverable message n be the same as the entire message msg.

Definition 1. (Message recovery signature scheme) A message recovery signature scheme consists of three probabilistic polynomial-time algorithms (G, S, V).

– G is a key generation algorithm that takes security parameter λ and outputs a public-key pk and a private-key sk. Associated with pk is a recoverable message space {0, 1}^rec.

– S is a signature-issuing algorithm that takes a private-key sk and a message msg and outputs a signature σ and the non-recoverable part of the message n.

– V is a verification protocol that takes a public key pk and a signed message (σ, n) and outputs (accept, msg) or reject. It is required that (accept, msg) = V(pk, S(sk, msg)) for any pk and sk generated by G and for any msg.

A message recovery signature scheme is secure if it withstands an adversary that asks a legitimate signer to sign arbitrary messages and then attempts to forge a valid signed message never signed by the signer. Formal definition of such a chosen message adversary follows.

Definition 2. (Chosen message adversary) A (τ_sig, ε_sig, q_s, q_h) chosen message adversary A_sig against the above message recovery signature scheme is an oracle Turing machine that launches a chosen message attack that consists of the following steps.

1. (pk, sk) ← G(λ)

2. (˜σ, ˜n ) ← A_sig^S,H(pk)

S is the signing oracle such that, for every signing query for a message, say msg_i, it returns a legitimately generated signed message (σ_i, n_i) by using private key sk. H is the random oracle that corresponds to hash function H in the signature scheme. Let T denote the signed messages (σ_i, n_i) observed by S. The final output of A_sig must satisfy (˜σ, ˜n ) T. A_sig makes at most q_s queries to S and at most q_h queries to H and then stops within running time τ_sig. Then, V(pk, ˜σ,˜n ) outputs (accept, msg) for some msg with probability at least τ_sig. The probability is taken over all the random coins used in the chosen message attack.

3.1 Redundancy function

The heart of our construction is the redundancy function, say Δ: Dom(A) × {0, 1}^rec → D, that takes the first message a of the underlying sigma-protocol and a recoverable part of the message m and outputs a redundant message r in some specific domain D. More precisely, we assume a family of functions Δ_λ = {Δ} and its ensemble {Δ_λ}_λ∈N that satisfy the following properties.

1. (Invertibility) For every Δ, there exists an inverse function Δ⁻¹ that, given (a, r), outputs m. It is required that m = Δ⁻¹(a, Δ(a, m)).

2. (Compactness) BitLen(Dom(A)) + _rec ≥ BitLen(D).

3. (Randomness) For every Δ and every m, the distribution of Δ(a, m) for uniformly chosen a is uniform.

4. (Collision resistance) Given Δ ← Δ_λ, any probabilistic algorithm running within time τ finds (a, m) and (a′, m′) such that Δ(a, m) = Δ(a′, m′) and (a, m) ≠ (a′, m′) only with probability, say ε_Δ^coll(τ), which is negligible in λ if τ is polynomial in λ.

Invertibility is needed for our construction to work. Compactness is needed for the message recovery property to be meaningful. Without this property, the signed message of the resulting message recovery signature scheme would be longer than the one from the signature scheme with appendix. Randomness and collision resistance are needed for unforgeability of the resulting signature scheme.

One can relax the randomness property to be computationally indistinguishable from uniform. This will affect the unforgeability of the resulting signature scheme, as we mention later.

As we shall see in Section 4. ε_Δ^coll(τ) may take some other parameters such as the maximum number of oracle queries, depending on its construction.

3.2 Our scheme

Given a sigma-protocol (A, C, Z, V, E, M) for L and a hash function H, we construct a message recovery signature scheme (G, S, V) as follows.

– (Key generation: G) Given λ, run (x, w) ← L(λ) and output x as a public key and w as a private key. Security parameter λ also determines the length of the recoverable part _rec and the redundancy function Δ.

– (Signature generation: S) Given private key w and message msg, first chop msg as msg = m||n so that m_∈ {0, 1}^rec. Then, compute a ← A(x; t), r ← Δ(a, m), c ← H(r, n), and z ← Z(w, t, c). Then, output (r, z, n) as a signed message.

– (Signature verification: V) Given x and (r, z, n), compute c ← H(r,n), a ← V(x, c, z), and m ← Δ⁻¹(a, r). If r ← Δ(a, m), output (accept, m||,n). Otherwise, output reject.

Implementation note. Depending on the specific structure of function Δ, the signature verification can be more efficient than recomputing Δ. See also Subsections 4.1 and 4.2.

3.3 Proof of security

Theorem 1. (Security against chosen message attacks) If there exists (τ_sig, ε_sig, q_s, q_h)-adversary A_sig for the message recovery signature scheme based on language L and an instance generator L, then there exists a (τ_w, ε_w) witness extraction adversary A_L, where τ_w ≤ 8τ _sim /,(ε_sig − 4 )

and ε_w ≥ . (1 − ) (1 − ε^coll_{Δ, sim}).

Here, τ_sim is τ_sig + q_sT_sig, where T_sig is the sum of the running times of C, M, and Δ, and ε^coll_{Δ, sim} is ( − ) −1ε_Δ^coll (2τ_sim).

Proof. This is proved by constructing A_L from A_sig using a forking lemma in a standard manner. Let x∈L be an instance generated by L(λ). Given x as input, A_L works as follows.

1. Invoke A_sig with x as a public key and a uniformly chosen random tape. If A_sig terminates with a valid signed message (˜r,˜z, ˜n), proceed to the next step. Otherwise, repeat this step with the same x and a fresh random tape up to t₁ times. Abort if never successful. Oracle queries are handled as follows.

– (Query msg_i to S.) Execute c_i ← C(x) and (a_i, z_i) ← M(x, c_i). Then, chop msg_i into m_i||n_i, compute r_i ← Δ(a_i, m_i), and define H so that c_i = H(r_i, n_i). If H has already been defined for such an input, abort. Otherwise, return (r_i, z_i, n_i) as a signed message.

– (Query (r_j, n_j) to H .) If the input is fresh, select c_j uniformly, define H as c_j = H(r_i, n_i), and return c_j. Otherwise, return the preliminarily defined value.

2. Let i^* denote the index that H is asked (˜r, ˜n ). That is, r_i* = ˜r, n_i* = ˜n, and c_i* = H(˜r, ˜n). Let ˜a denote ˜a ← V(x, c_i*, ˜z). Move to the next step.

3. Invoke A_sig with x and the random tape used in the successful run of the first step. The simulation for oracle S is unchanged. Oracle H is simulated identically up to the point that (˜r, ˜n )) is asked. From that moment, H is simulated with new randomness. If A_sig terminates with a valid signed message (˜r, ˜z′, ˜n ), then proceed to the next step. Otherwise, repeat this step up to t₂ times. Abort if never successful.

4. Let c′_i* =H(˜r, ˜n), which was observed in the second step, and let ˜a′ be ˜a′← V(x, c_i*′ , ˜z′). If c_i* = c′_i* or ˜a ≠ ˜a′, abort. Otherwise, compute w ← E(x, ˜a, c_i*, ˜z, c′_i* , ˜z′) and output w.

Now we estimate the running time and the probability of success of A_L. First, the success probability is estimated as follows.

– First, we estimate the error probability of the oracle simulation. Observe that the simulation of S fails only if (r_i, n_i) has already been defined for H. Since the distribution of n_i is arbitrarily determined by the adversary, we consider only the sufficient condition that r_i has appeared so far.

Suppose that r_i is uniformly chosen from D. Then, the probability that r_i has appeared among the inputs to H is at most q_h/|D|.

Next consider r_i generated through Δ from uniformly chosen a_i. Since we assume that the distribution of the output of Δ is uniform, the above probability does not change at all. (This is where the relaxation of randomness on Δ would have an effect. If the randomness is not perfect but just indistinguishable with some advantage, say ε^dist_Δ(τ) for a polynomial-time distinguisher whose running time is , then the error probability of the simulation increases by ε^dist_Δ(τ_sim).)

Then, consider a_i generated by M. As in the previous step, since the distribution of such a_i is perfectly the same as uniform, the error probability does not change at all, either. (Again, this is where the relaxation on the zero-knowledge property of the underlying sigma-protocol matters. If the zero-knowledge simulation is only computational with some advantage, say at most ε_zk(τ) for a distinguisher whose running time is τ, then the error probability increases by ε_zk(τ_sim).)

Therefore, the probability ε_serr that the simulation fails while handling q_s queries is bound as

The simulation of random oracle H is obviously perfect unless the simulation of S fails.

– The success probability of A_sig for fixed x is at least ε_sig/2 with probability 1/2 (over the choice of x) due to the heavy-row lemma of [15], [18]. With the simulated signing oracle, the success probability reduces to ε_sig/2 − ε_serr. Accordingly, every run of A_sig in the first step is successful with probability at least μ₁: = (ε_sig/2 −ε_serr). By repeating the attempt up to t₁: = 1/μ₁ times, we get at least one valid (˜r, ˜z, ˜n ) at the end of the first step with probability greater than ε₁ ≥1− (1 − μ₁)^1/μ₁ ≥ 1 − e<⁻¹ ≥ 3/5. Let Θ* denote the randomness used for simulating the random oracle for the i*-th and all subsequent queries in the successful run. Let Θ^* denote all other randomness also used in the successful run.

– Over the choice of Θ^*, the success probability of A_sig for fixed Θ and x is at least ε_sig/4 with probability 1/2 (over the choice of Θ) due to the heavy-row lemma again. If we apply the same argument as in the first step, each attempt in the third step is successful with probability at least μ₂: = ε_sig/4 − ε_serr. If we repeat this attempt up to t₂: = 1/μ₂ times, another valid signed message (˜r′, ˜z′, ˜n′;) is obtained with probability greater than ε₂ ≥ 1 − (1 − μ₂)^1/μ₂ ≥ 1 − e⁻¹ ≥ 3/5. Furthermore, the outcome corresponds to the i^*-th query to H, i.e., ˜r′ = ˜r and ˜n′ = ˜n, with probability at least 1/q_h.

– In the fourth step, c_i* = c′_i* happens only with probability 1/|C|. Observe that, if ˜a ≠ ˜a′, then we have ˜r = Δ(˜a, Δ⁻¹(˜a, ˜r)) = Δ(˜a′, Δ⁻¹(˜a′, ˜r)) which is a collision. Let ε^coll_Δ,sim, denote the probability of such an event occurring. Since the running time of A_L is less than τ_w= (t₁ + t₂) τ_sim, ε^coll_{Δ, sim}, collsim can be upper bounded by ε^coll_{Δ, sim}(τ_w). It is, however, an overestimation. More precise estimation of the probability is at most

because we have at most t₁ trials for an independent choice of Δ, and the particular Δ chosen in the successful run in the first step is executed again in the third step of the simulation and the total running time with this particular Δ is 2τ_sim.

By summing up the above assessment, we get the total success probability of A_L as

Assuming that the time for generating randomness and table searching used for simulating H is free, the running time is

4.1 In the random oracle model

We construct Δ and Δ⁻¹ as follows.

H₁: {0, 1}^* → {0, 1}¹ and H₂: {0, 1}^* → {0, 1}^rec are hash functions modeled as independent random oracles.

To make the message recovery property meaningful, ₁ < |a| should hold. Note that, as we shall show in Lemma 2, setting _rec too short would cause a security problem, i.e., it would result in a high probability of collision. Recommendable settings of ₁ and _rec are ₁ = _rec = |a|/2 to balance security and the benefit of message recovery. If one would like the length of the recoverable part to vary depending on the given message, the message must be polynomially long or some kind of padding must be applied so that the total length becomes polynomial in λ.

With the above instantiation, the verification procedure specified in Subsection 3.2 can be slightly more efficient. The modified signature verification procedure is as follows.

– (Signature verification: V) Given x and (r, z, n), compute c ← H(r, n), a ← V(x, c, z), and m ← Δ⁻¹(a, r). Then, let h₁||h₂ ← r. If h₁ = H₁(a, m), output (accept, m||n). Otherwise, output reject.

Namely, it replaces the testing r = Δ(a, m) with h₁ = H₁(a, m) and saves one computation of H₂.

The above Δ satisfies the required properties listed in Subsection 3.1. Specifically, the following lemmas hold. The first three (invertibility, compactness, and randomness) are trivial and the last one (collision resistance) is followed by a detailed proof.

Lemma 1. (Invertibility, compactness, and randomness) The above Δ is invertible. In particular, the above Δ⁻¹ is the inverse function. It is compact when ₁ is set so that BitLen(Dom(A)) ≥ ₁. The output distribution of Δ is uniform over {0, 1}_¹+_^rec if H₁ and H₂ are independent random oracles.

Lemma 2. (Collision resistance) If ₁ and _rec are polynomial in λ, the above Δ is collision resistant against polynomial-time adversaries that make a polynomial number of queries to H₁ and H₂. In particular, for any adversary asking q₁ and q₂ queries to H₁ and H₂, respectively, the probability of collision is upper bounded by ∈_Δ^coll(q₁, q₂) ≤ + + + . + .

Proof. (of Lemma 2) We refine the notation for the input and output of H₁ and H₂ as follows. Let h_i = H₁(R_i, M_i) and c_j = H₂(D_j, e_j) denote the i-th and j-th input/output of H₁ and H₂, respectively. We first define the notation and some terminology. Let L₁ denote the set of queries and answers for H₁, i.e., L₁ = {(R_i, M_i, h_i)|i = 1, ..., q₁}. Define L₂ = {(D_j, e_j, c_j)| j = 1, ..., q₂} as well. Without loss of generality, we assume that every query is fresh, so every entry in L₁ and L₂ is unique. By (i, j), we denote a set that consists of the i-th entry of L₁ and the j-th one of L₂, i.e., (i, j) = (R_i, M_i, h_i, D_j, e_j, c_j). We say that (i, j) is fully consistent if (R_i, h_i) = (D_j, e_j). Note that if (i, j) is fully consistent, it forms a correct computation of Δ. By FullCon (i, j) = true or false, we mean that (i, j) is or is not fully consistent, respectively. We also say that (i, j) is semi-consistent if R_i = D_j. A semi-consistent (i, j) may also be fully consistent but this is not necessary. By SemiCon(i, j) = true or false , we mean that (i, j) is or is not semi-consistent, respectively. Let τ(H_b, i) for b ∈1, 2 denote the time at which the i-th query is made to H_b. (It can be understood as the number of steps before the i-th query is made to oracle H₁). Since no more than one query can be made at one step, τ(H_b, i) is strictly larger or smaller than τ(H_b′, i′) if i ≠ i′. We say that (i, j) is regular if τ(H₁, i) < τ(H₂, j); otherwise, it is irregular. The intuition behind this terminology is that anyone who computes Δ correctly should ask H₁ first and then H₂ in that order. Therefore, a normal computation of Δ yields regular and fully consistent (i, j). By Regular(i, j) = true or false , we mean that (i, j) is regular or irregular, respectively. We define function X(i, j) as X(i, j) = c_j ⊕ M_i.

With this terminology, we can say that a collision Δ(R_i, M_i) = Δ(R_u, M_u) happens if and only if there exist j and υ such that

– (i, j) ≠ (u, υ),

– FullCon(i, j) = FullCon(u, υ) = true, and

– h_i||X(i, j) = h_u||X(u, υ).

Accordingly, we say that (i, j) and (u, υ) collide if and only if the above conditions are satisfied. By Collision(i, j, u, υ) = true or false , we mean (i, j) and (u, υ) do or do not collide, respectively.

We classify entries in L₂ by the value of e_j. Namely, for every different value of e_j in L₂, we consider a set of indexes {υ|e_υ = e_j} and label such sets as Class₁, Class₂, .... In this way, every entry in L₂ is associated with one class. Obviously, there are at most q₂ classes. Let SameClass( j, υ) be true if and only if j and υ are in the same class, i.e., e_j = e_υ.

The above definitions lead simply to some facts.

Fact 1. If SameClass( j, υ) = false, then Collision(i, j, u, υ) = false.

If two consistent (i, j) and (u, υ) are in different classes, then h_i = e_j ≠ e_υ = h_u holds and they cannot collide. Moreover, if either of them is inconsistent, it cannot have a collision, either. Therefore, we consider the possibility of collision only within a class.

Fact 2. |{(i, j)|FullCon(i, j) = true}| ≤ q₁.

Namely, there are at most q₁ pairs of fully consistent queries. Suppose that (i, j) is fully consistent and (i, j′) is also fully consistent for some j′. Then, e_j = h_i = e_j′ and D_j = R_i = D_j′ holds, and it means that the j-th and j′-th queries to H₂ are identical, whereas we assumed that L₂ contains no duplicate entries.

Fact 3. |{(i, j)|SemiCon(i, j) = true, ∧j∈Class_k}| ≤ q₁ for every Class_k.

Namely, there are at most q₁ semi-consistent pairs of queries with regard to each class of L₂. Suppose that (i, j) and (i, j′) are both semi-consistent and j and j′ are in the same class. We then have D_j = R_i = D_j′ and e_j = e_j′. Hence, the j-th and j′-th entries in L₂ are identical.

Suppose that (i, j) and (u, υ) are both semi-consistent and they are in the same class. These queries can collide. (On the other hand, if either of them is not semi-consistent or if they are in different classes, they cannot collide.) Regarding the regularity of (i, j) and (u, υ), one of the following cases must be true.

Case 1. Both are regular.

Case 2. One is regular and the other is irregular.

Case 3. Both are irregular.

A pair of regular queries, say (i, j), is either fully consistent (the case where (R_i, h_i) is the input (D_i, e_i) to H₂) or inconsistent (something else is given as input to H₂). These cases are independent of the choice of the randomness of H₁ and H₂. If (i, j) is regular but inconsistent, there is no chance of it causing a collision with another pair of queries. Hence, we only need to consider fully consistent queries in the regular case. Below, we consider the probability of collision in each of the above cases.

Case 1. Consider regular and fully consistent queries (i, j) and (u, υ) in the same class. For a collision to occur, h_i = h_u and c_j ⊕ M_i = c_υ ⊕ M_u are necessary. First of all, h_i = h_u happens with probability at most because both h_i and h_u are uniformly chosen as a result of the true randomness of H₁ and H₂. Next, consider c_j ⊕ M_i = c_υ⊕ M_u. Since (i, j) and (u, υ) are regular, τ(M_i) < τ(c_j) and τ(M_u) < τ(c_υ) hold. Therefore, at least one of c_j and c_υ is independent of M_i and M_u. Since both c_j and c_υ are chosen uniformly, c_j ⊕ M_i = c_υ ⊕ M_u holds with probability at most . Thus, (i, j) and (u, υ) collide with probability at most . Let FullCon(Class_k) denote the number of fully consistent queries in Class_k. By summing up the probability for all the classes and applying Fact 2, we get

Case 2. For every entry i in L₁, there exists at most one entry, say j, in each class of L₂ such that (i, j) is semi-consistent. (If there exists j′ in the same class such that (i, j′) is semi-consistent, then j = j′ because R_i = D_j = D_j′ and e_j = e_j′.) We consider the probability that the semi-consistent (i, j) in the class is irregular and collides with a regular and fully consistent (u, υ) in the same class. First of all, (i, j) must be fully consistent to have a collision. Therefore, it must satisfy h_i = e_j when h_i is randomly and independently chosen, which in turn happens with probability at most . Second, c_j ⊕ M_i = c_υ ⊕ M_u must hold. Since (i, j) is irregular, however, M_i can be set after the values of c_j, c_υ, and M_u have been seen, and this condition can be satisfied with probability 1 by setting M_i as M_i = c_j ⊕ c_υ ⊕ M_u. Note that there is only one regular and fully consistent (u, υ) in the class that causes c_j ⊕ M_i = c_υ ⊕ M_u with (i, j). Otherwise, there would exist another regular and fully consistent (u′, υ′) in the same class and it would cause c_j ⊕ M_i = c_υ′ ⊕ M_u′. Then, (u, υ, u′, υ′) would have a collision. This has already been treated in Case 1.

One question is whether or not such a manipulated M_i can also be a candidate for a collision in other classes. We claim that if (i, j) in Class_k has (u, υ) in Class_k that satisfies c_j ⊕ M_i = c_υ ⊕ M_u, then (i, j′) in Class_k′ has (u′, υ′) in Class_k′ that also causes c_j′ ⊕ M_i = c_υ′ ⊕ M_u′ only with probability . (Naturally, we suppose (i, j′) is irregular and semi-consistent and (u′, υ′) is regular and fully consistent so they fall into Case 2.) This happens only if

Since (u, υ) and (u′, υ′) are regular, all c_j c_υ ⊕ M_u c_j′, and c_υ′ ⊕ M_u′ are random and independent of each other. Hence, E_q.(11) is satisfied only with probability .

In summary, with regard to each query i in L₁, we have a collision probability of at most +≤ + . Summing up the probabilities for all i in L₁, we get the upper bound of the probability for Case 2 as

Case 3. We consider the probability that, for an irregular semi-consistent query (i, j) in a class, there exists another irregular semi-consistent query (u, υ) in the same class that causes a collision.

First of all, (i, j) itself must be fully consistent. This is satisfied with probability at most . In addition, (u, υ) must be fully consistent and this happens with probability at most .

Next, we consider the number of (u, υ) in the class, say Class_k, that collide with (i, j) with nonzero probability. We first claim that if j =υ , then (i, j) and (u, υ) cannot collide. Suppose that j =υ . Since both (i, j) and (u, υ) are semi-consistent, R_i = D_j = D_υ = R_u holds.

Since (i, j) and (u, υ) are distinct, (R_i, M_i) ≠ (R_u, M_u), so M_i ≠ M_u. If a collision happens, c_j ⊕ M_i = c_υ ⊕ M_u must hold. But this is not possible because cj = cυ and M_i ≠ M_u. We next claim that if (i, j) and (u, υ) satisfy c_j ⊕ M_i = c_υ ⊕ M_u, then no other (u′,υ ) in the same class can cause c_j ⊕ M_i = c_υ ⊕ M_u′. The reason is essentially the same as for the above claim. Since both (u, υ) and (u′, υ) are semi-consistent and in the same class, M_u ≠ M_u′ must be the case (otherwise, u and u′ are the same query in L₁). Hence, c_j ⊕ M_i = c_υ ⊕ M_u = c_υ ⊕ M_u′ cannot happen. From the above two claims, we can see that, for (i, j), and for every υ in Class_k, there could exist at most one u that makes (i, j, u, υ) have a collision. Namely, there are at most |Class_k| — 1 candidates of (u, υ) that have nonzero probability of collision with (i, j).

In summary, for every irregular semi-consistent (i, j), the probability that there exists an irregular semi-consistent (u, υ) that causes a collision is at most . . From Fact 3, we have at most q₁ candidates of such (i, j) in a class. Thus, the probability of collision in each class is at most . . Summing up the probabilities for all classes and applying Σ_k |Class_k| ≤ q₂, we get

Summary. From the bounds shown as in the Eqs. (10), (12), and (13), we get

as stated.

4.2 In the ideal cipher model

Let (SG, SE, SD) be a symmetric encryption such that: SG is a probabilistic algorithm that takes security parameter λ and outputs a secret key sk, SE is a (probabilistic) algorithm that encrypts input message msg and outputs a ciphertext ξ by using secret key sk, and SD is a decryption algorithm that takes ciphertext ξ and recovers plaintext msg by using secret key sk.

We model a symmetric encryption scheme as an ideal cipher in the following

– SE and SD are oracles.

– Given a query (sk, msg), oracle SE does the following. If (sk, |msg|) is not recorded in Π, an initially empty list, select a new random permutation RP: {0, 1}^|msg| → {0, 1}^|msg| and return RP(msg). Then, record (sk, |msg|, RP) to Π. If (sk, |msg|) is in Π, simply return RP(msg) using the corresponding RP. Oracle SD does the reverse. That is, given a query (sk, ξ), if (sk, |ξ|) is not in Π, select a new random permutation RP: {0, 1}^|ξ| → {0, 1}^|ξ|, record (sk, |ξ|, RP) in Π, and return RP⁻¹(ξ). If (sk, |ξ|) is in Π, simply return RP⁻¹(ξ) using the corresponding RP.

We now construct Δ and Δ⁻¹ as follows. Let str be a sufficiently long fixed string.

Without loss of generality, we assume that SG takes randomness from the domain of a in the above construction. (Otherwise, a is preprocessed with an entropy smoothing method and then given to SG.) The output of SD is separated into two parts so that the length of the first part equals the length of the prefixed string str and the remaining part is taken as a recovered message.

In Δ⁻¹, the recovered str is not used at all. It can be used to make the verification procedure slightly more efficient as follows.

– (Signature verification: V) Given x and (r, z, n), compute c ← H(r, n), a ← V(x, c, z), and m ← Δ⁻¹(a, r). Then, let υar be the string obtained while computing Δ⁻¹. If υar = str, output (accept, m||n). Otherwise, output reject.

Namely, it verifies whether or not the predetermined string str is recovered correctly.

We claim that the above construction conforms to our requirements. Again, the first three requirements are obviously satisfied. Collision resistance is stated with a proof below. Let _str be BitLen(str).

Lemma 3. (Invertibility, compactness, and randomness) The above Δ is invertible. In particular, the above Δ⁻¹ is the inverse function. It is compact when _str is set to _str ≤ BitLen(Dom(A)). The output distribution of Δ is uniform over {0, 1} ^{_str + _rec}.

Lemma 4. (Collision resistance) If _str and _rec are polynomial in λ, the above Δ is collision resistant against polynomial-time adversaries that make a polynomial number of queries to SE and SD. In particular, for any adversary asking q_d and q_e queries to SE and SD, respectively, ∈_Δ^coll ≤ + holds.

Proof. Observe that a collision happens only if

– there exists at least one pair of the same value among the returned values from SE or

– there exists a message returned from SD whose leading part is str.

The probability of the former case is upper bounded by as a result of the birthday paradox among at most q_e randomly selected return values from SE. Since every value returned from SD is random, the probability that the second case occurs when at most q_d queries are asked is at most . Summing up these bounds gives the upper bound as stated.

From these lemmas, recommendable settings would be _str = _rec = BitLen(Dom(A))/2 to balance the efficiency of the message recovery property and unforgeability.

With this instantiation of the Δ function and the Schnorr identification scheme defined over a group over an elliptic-curve as the underlying sigma-protocol, the resulting message recovery signature scheme turns out to be the ECPV scheme presented in [12].