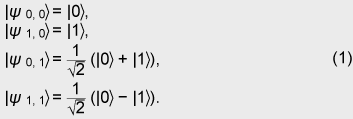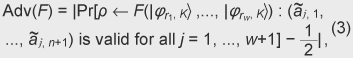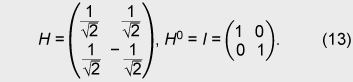|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Vol. 6, No. 1, pp. 29–36, Jan. 2008. https://doi.org/10.53829/ntr200801sp3 Quantum Voting Scheme Based on Conjugate CodingAbstractWe describe a quantum voting scheme in which a ballot is an unknown quantum state for a voter. Such a ballot is hard to forge because it is difficult in principle to make a copy of an unknown quantum state. Moreover, our quantum voting scheme guarantees anonymity because the ballot can be randomized by voters. We also describe a distributed variant of our scheme that is robust against a dishonest administrator. This scheme should remain usable in the coming era of quantum computers, which are expected to break most existing cryptographic schemes.
1. IntroductionThere are several types of voting systems. Open ballot voting is a system in which voters write their own names on their ballots for self-identification and to prevent double voting. In such a voting system, the privacy of the voters is not guaranteed. If voter privacy is desired, an anonymous voting system is better than open ballot voting. To achieve fair anonymous voting, the voting scheme should satisfy the following requirements.
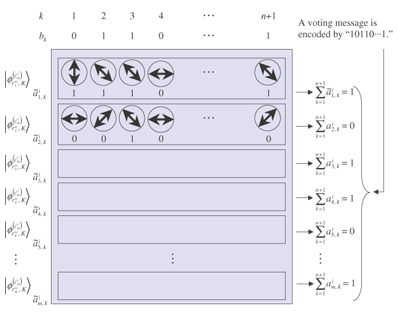
Unlike in open ballot voting, in anonymous voting we need to achieve correctness while keeping anonymity. Since this is a challenging issue for cryptography, there has been a lot of research on cryptographic anonymous voting schemes. However, almost all existing practical electronic voting schemes that satisfy these requirements are based on the computational complexity assumption of discrete logarithm or integer factoring, which will be broken by quantum algorithms. Therefore, when a quantum computer is made in the future, we will lose almost all our practical electronic voting schemes. On the other hand, quantum information technology (QIT), which includes quantum communications and quantum computation, should be suitable for constructing a voting scheme because it is difficult to make a copy of an unknown quantum state in quantum physics. That is, if an unknown quantum state is used for a ballot, it is hard to forge, which is very suitable for a voting scheme. In this paper, we describe the new concept ofquantum voting. The anonymity of the protocol is guaranteed unconditionally because the ballots can be randomized by voters. Correctness, i.e., the one-voter one-vote principle, is guaranteed by a quantum complexity assumption called one-more unforgeability, which means that it is impossible to forge an additional valid ballot. We also present a cut-and-choose protocol and a distributed protocol for preventing the administrator from dishonestly executing procedures. In a distributed version of our scheme, no central entity (center) knows enough of the whole secret to issue blank ballots, which is better in terms of keeping secrecy. 1.1 Related workQuantum voting: There have been a few proposals of quantum voting schemes [1], [2] for specialized situations. The key technique of these voting schemes is distributing quantum entanglement for obtaining anonymity. Unlike those schemes, ours does not use quantum entanglement, so it should be easier to achieve and be more flexible for various circumstances. Electronic voting: There have been many proposals of classical electronic voting schemes. They can be classified into three approaches: (1) blind-signature-based schemes [3]–[5], (2) mix-net-based schemes [6]–[10], and (3) homomorphic-encryption-based schemes [11]–[14]. Some of these achieve receipt-freeness [12] under the assumption of a one-way untappable channel [5], [8], [15] or two-way untappable channel [12], [16], [17]. 2. Our quantum voting schemeLetH be a 2-dimensional Hilbert space, i.e., the space of a 1-qubit state and letH The value of b determines the basis: if b is 0, then a is encoded in basis Z; if b is 1, then a is encoded in basis X. This encoding is the same as BB84 quantum cryptography [18] or conjugate coding [19]. Similarly, the qubit measurement is performed in basis Z or X if the measurement basis b is specified to be 0 or 1, respectively. For basis K = (b1, ..., bn+1) ∈{0, 1}n+1 and r = (a1, ..., an+1) ∈{0, 1}n+1, we denote We call state For the measurement of an (n+1)-qubit state ρ ∈ H 2.1 One-more unforgeabilityNow, we define the one-more-unforgeability assumption, on which our quantum voting scheme is constructed. We consider the following game involving adversary F that models an adversarial voter who tries to forge blank pieces, i.e., tries to create a total of (w + 1) blank pieces when given w blank pieces. Let adversary F be a polynomial-time quantum Turing machine and n be a security parameter. At the beginning of the game, basis K = (b1, ..., bn+1) ∈ {0, 1}n+1 is selected uniformly. Adversary F is given w (which is polynomial in n) blank pieces We define the advantage Adv(F) of adversary F as Assumption. (One-more unforgeability) We say that the one-more unforgeability assumption holds if, for every polynomial-time quantum adversary F, the advantage Adv(F) is negligible with respect to security parameter n. 2.2 Quantum voting protocolIn this subsection, we describe our quantum voting protocol. The anonymity of this protocol is guaranteed unconditionally, and correctness is guaranteed if the one-more-unforgeability assumption holds. Let n be a security parameter and m = O(n) be the bit length of the voting message. There are an administrator A, counter C, and υ voters Vi (i = 1, ...,υ). We assume (1) an authenticated channel, where sender and receiver are authenticated, from administrator A to voter Vi and (2) a sender-anonymous channel, where the sender is anonymous and the receiver is authenticated, from voter Vi to counter C. For simplicity, we assume that these channels are secure, i.e., error-free. Counter C is assumed to carry out protocols correctly; otherwise, the result of voting could be manipulated as C desired. C just acts as a fair procedure and other aspects of security do not especially depend on his existence, i.e., C does not have any secrets of his own and all results of measurement are published. Issuing. Administrator A uniformly selects a secret K = (b1, ..., bn+1) ∈{0, 1}n+1. Then, for i = 1, ..., υ, administrator A selects ri = (ri1, ..., rim) = (ai1, 1, ..., ai1, n+1, ..., aim, 1, ..., aim, n+1) ∈{0, 1}m(n+1), where aij, 1 ... aij, n (j = 1, ..., m) are selected uniformly and aij, n+1 = aij, 1 ⊕ ... ⊕ aij, n (j = 1, ..., m), and constructs a blank piece A blank ballot is depicted in Fig. 1. Administrator A sends the blank ballot
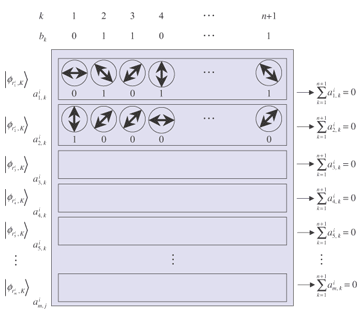
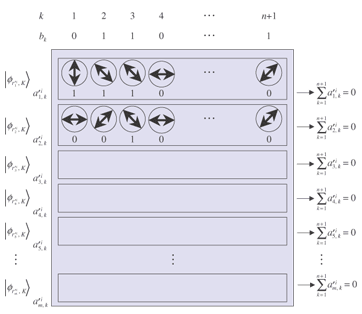
Randomization. Voter Vi receives the blank ballot Ydij, n+1, where Y = XZ = A randomized blank ballot is depicted in Fig. 2.
Remark: The unitary transformation Y flips a for both bases Z and X. Sometimes, it also changes the global phase, but no one can distinguish the difference in global phase. Consequently, the global phase change caused by Y does not affect the user's anonymity. Remark: Since each blank ballot has a randomly chosen pattern of information ri, if a voter utilizes a blank ballot without any modification, the administrator may be able to trace the ballot by recording ri, so the voter's privacy cannot be guaranteed. Voting. Let M ⊂ {0, 1}m be the set of all the valid voting messages, where the number of valid voting messages |M| is constant for security parameter n and m = O(n), so the probability that a random bit string becomes a valid voting message is negligible for n. On the randomized blank ballot
Counting. Counter C receives secret K from administrator A through a classical secure channel after all voters have sent their votes. He receives all ballots 2.3 Cut-and-choose protocol for issuingIf a malicious administrator issues invalid blank pieces, correctness and anonymity can be violated because the administrator can nullify and/or trace a ballot by mixing invalid pieces into it. To avoid the risk of this, we can use a cut-and-choose technique to verify the validity of blank pieces issued by the administrator. Our cut-and-choose protocol is explained below. In the issuing stage, administrator A creates 2mυ blank pieces Before the counting stage, after all voters have cast their votes, counter C receives secret K from administrator A through a classical secure channel and performs the following check. Counter C measures mv blank pieces left in register R using secret basis K and checks whether or not all the results of these measurements are valid. If some are found to be invalid, we judge that administrator A issued invalid blank pieces and abort the voting process. Note that a malicious administrator can mingle a small number of invalid blank pieces into a voter's blank ballot without detection even if we use the cut-and-choose protocol. 2.4 The t-out-of-l threshold protocol for issuingHere, we present a threshold distributed protocol based on threshold quantum cryptography. If an administrator who knows secret K illegally casts a valid voting ballot in the voting stage, or dishonestly gives secret K to adversaries, then the adversaries can freely forge ballots as they like. To avoid the risk of this, a distributed scheme is very effective. In such a scheme, several centers each hold a share of secret K, and these centers collaborate to create blank pieces. In this t-out-of-l threshold distributed protocol, each center chooses its secret by itself and distributes shares of its own secret. Once the secrets have been shared among l centers, an arbitrary t-out-of-l centers can issue valid blank pieces. After the preliminary secret distribution phase, even if l−t centers happen to be down or out of service, at least t centers will still work properly, so the whole scheme works correctly. Moreover, if the number of dishonest centers is smaller than t, they cannot make valid quantum ballots. We apply a threshold technique such as Shamir's secret sharing scheme [21] (i.e., t-out-of-l scheme) for this threshold distributed protocol. We also apply Pederson's idea [22] that several centers share their own secrets. Distribution. For l centers to distribute shares of their secrets, all centers Pj out of the l centers perform the following procedure. Pj chooses its own secret σj = (bj,1, bj, 2, ..., bj,n+1), where bj, k are uniformly chosen from {0, 1}. The center Pj then makes l shares, Sj,1, ..., Sj, l, of σj by using Shamir's secret sharing scheme over GF(2N), where N = n+1. Let fj (x) be a secret (t−1)-th-degree polynomial, Sj,i = fj (xj, i) for i = 1, ..., l, and σj = fj(0) over GF(2N), where xj, i for i = 1, ..., l are l distinct points in GF(2N) and are published. The center Pj sends Sj, i to a center Pi secretly for each i = 1, ..., l. Precomputation. For simplicity, we assume that the t centers P1, ..., Pt collaborate to issue blank pieces. For each i = 1, ..., t, Pi calculates and secretly stores the following value using the Lagrange interpolation formula Let Note that even in the collaboration procedure, Ki and σj are kept secret in Pi, and K is not recovered. Issuing. The t centers P1, ..., Pt collaborate to construct a blank piece P1 generates a quantum state Next, P1 sends Then, Pi obtains where Here, a[i]n+1 = a1[i] ⊕ ... ⊕ an[i], r[i] = (a1[i], ..., an[i]), ∈{0, 1}n is a random string uniformly picked by Pi for each blank piece, unitary transformation Y follows the previous definition in Subsection. 2.2, and After repeating this procedure, finally Pl sends Correctness. Security. If we assume that the communication among l parties during their collaboration is protected from adversaries and that the l parties are honest, then the security of the threshold scheme is at least on the same level as the original voting scheme. 3. Security of our quantum voting scheme3.1 Security considerations for voting requirementsCorrectness. First, we consider an active attack by a voter who tries to forge ballots. In this case, security will depend on the quantum computational complexity problem, i.e., one-more unforgeability (the Assumption in Subsection 2.1), whose hardness is not clearly understood yet, so conclusive security is beyond the scope of this paper. Here, we show that several naïve attacks cannot work well. It is impossible to simply make a copy of an unknown quantum state in principle according to the no-cloning theorem. If a forger (including a voter) tries to make a quantum ballot without knowing secret K, i.e., randomly makes a forged quantum ballot, the forged ballot Next, we consider an active attack by the administrator. If the administrator mixes k invalid blank pieces into 2mv blank pieces in the issuing stage, we can detect invalid blank pieces with probability 1–1/2k using our cut-and choose protocol for issuing. If an invalid blank piece is detected, we abort the voting. The invalid blank pieces pass through the checking stage with probability 1/2k, so in this case, the administrator can nullify at most k unspecified votes. Anonymity. A voter cannot break the privacy of another voter because he is isolated from the other voter's procedures and the communication channels are protected to make them secure. Thus, we consider only an active attack by the administrator. Since all quantum voting ballots are sent through an anonymous channel, if there is no identifiable information in a ballot, then the privacy of voting is kept. The administrator can record randomness r encoded in blank ballot Although the administrator can mix k invalid blank pieces into 2mυ blank pieces in the issuing stage to trace votes and break privacy, we can detect the invalid blank pieces in the register with probability 1–1/2k using our cut-and choose protocol. If an invalid blank piece is detected, we abort the voting and discard the quantum voting ballots held by counter C. Therefore, in this case, votes are never revealed and privacy is protected. The invalid blank pieces pass through the checking stage with probability 1/2k. In this case, the administrator can invalidate at most k unspecified votes and break the privacy of at most k unspecified voters. Receipt-freeness. A voter might try to embed some information into his/her voting ballot A voter might try to copy his/her voting ballot 3.2 Intractability of finding secret key KLet us consider a straightforward individual attack on our voting scheme. An adversary F is given a blank ballot It has been pointed out that a Grover-type attack is applicable to this construction [23] if we allow F to use a general (coherent) attack. However, it still needs exponential time quantum computation. Grover's algorithm [24] has been proven to be optimal within the query-type algorithm to find a unique solution from a database [25]–[27]. Thus, F needs another type of algorithm to get secret bases efficiently, but no efficient attack has been found yet. In our scheme, the parity of random bits aj, 1 ⊕ ... ⊕ aj, n = aj, n+1 is encoded in 4. Concluding remarksIn this paper, we described a new cryptographic protocol concept, quantum voting. The anonymity of the protocol is unconditionally guaranteed, and correctness is guaranteed if the one-more-unforgeability assumption holds. We also presented a cut-and-choose protocol and a distributed protocol for preventing the administrator from dishonestly executing procedures. In this paper, we just assumed that the quantum channel is secure (error-free) for simplicity. We could eliminate this assumption by constructing a secure quantum channel using a quantum one-time pad [29], [30] or using some other means. We leave the analysis of quantum computational complexity as an open problem. Although the security of our protocol is based on quantum computational complexity and does not have unconditional security, it should have many applications in quantum information technology. To implement a quantum voting scheme, we need a quantum register/memory. Since our scheme does not make use of quantum entanglement, a sufficient register for our scheme is one of the most basic elements of quantum computers, that is, a 1-qubit register that need not keep quantum correlation between two quantum bits. (The situation will be different when we implement quantum error correction.) Even such a quantum register is still beyond our current technologies. However, such technologies are being extensively studied and developed. In addition, the operation needed for our scheme is very simple, only 1-qubit unitary transformation, which is already feasible. Finally, we emphasize that the use of a quantum state to achieve a voting scheme should be an attractive and fruitful research approach. The work described in this paper is the first step in this direction. References
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||