Entanglement Control of Superconducting Qubit Single Photon System

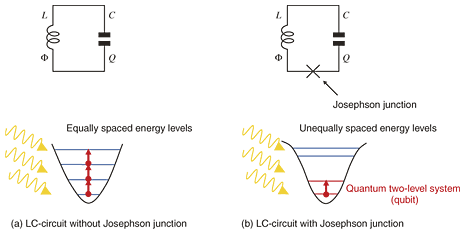
1. Artificial single quantum system

Thanks to the progress of microfabrication technology and nanosecond microwave pulse control techniques at dilution refrigerator temperatures, it has recently become possible to make and control an artificial single quantum system. Consequently, in a system of qubits interacting with a single-mode photon resonator, the superposition state and the entangled state have been reported, and efforts to control these states have already begun. As an example, I will mention progress in research related to the superconducting flux qubit system [1], [2].

There has long been a dream of applying these phenomena and technologies for quantum information processing, such as quantum simulation and quantum computation. In particular, for superconducting qubits, there is also fundamental interest concerning the issue of macroscopic quantum coherence [3].

Research on light and matter at the single-photon interaction level, cavity quantum electrodynamics (cavity-QED), has been performed using a single-mode high-Q cavity of an electromagnetic field together with an atom in the cavity. Theoretically, experiments of the same type have been considered to be possible in a superconducting circuit by replacing the atom by a superconducting qubit and replacing the cavity by a superconducting circuit [4]. This has recently been demonstrated in experiments. Furthermore, the interaction strength between a microwave photon and superconducting qubit has proved to be a few thousand times that of the well-known atom-photon interaction. The so-called strong coupling condition can be rather easily achieved in the superconducting circuit. Therefore, new parameter regions that are difficult to achieve with the ordinary atom/molecule cavity QED can be opened up by the cavity-QED in Josephson circuits on a chip.

2. Superconducting quantum bit

In normal metal, the continuous quasiparticle energy spectrum is located immediately above the Fermi energy. In contrast, in a typical S-wave superconductor, the continuous quasiparticle energy spectrum is located above the Fermi energy with a finite superconducting gap. If one could use the quantum levels in this superconducting gap, these states would be expected to be similar to the electronic state of a free atom, i.e., it is characterized by the long-lived discrete energy spectrum. In fact, if we make an LC (inductor-capacitor) circuit with superconducting material, the quantum energy levels in the superconducting gap will be available (Fig. 1). However, since the LC-circuit is equivalent to a harmonic oscillator, every energy level spacing has the same value h/(2π). All the levels can be excited by irradiating resonant microwaves. However, we cannot operate a pair of particular energy levels of the LC-circuit as a qubit. Therefore, we need Josephson junctions to introduce anharmonicity into the circuit. It is well known that the energy of the Josephson junction can be written as E = − E_J cosθ, where θ is the phase difference of the superconducting order parameter across the Josephson junction. Introducing the anharmonicity of the cosθ potential changes the energy level spacing to unequally spaced, as shown in Fig. 1(b). Here, we can manipulate the lowest two levels (qubit) by the resonant microwave pulses. The superconducting qubits can be classified into three characteristic groups, i.e., the phase qubit (E_J>>E_C), the flux qubit (E_J>E_C), and the charge qubit (E_J<E_C), where E_J is the Josephson energy of the junction and Ec is the charging energy of the junction [5]. Below, I introduce the superconducting flux qubit in detail because we are now doing research on flux qubits in NTT Basic Research Laboratories.

Fig. 1. Schematic energy levels of superconducting LC-circuit with or without Josephson junction.

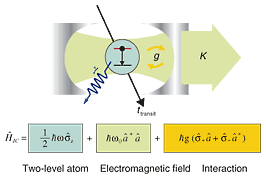
The superconducting flux qubit is a superconducting loop that incorporates sub-micrometer scale multiple (typically three) Josephson junctions on the sub-micrometer scale. Just like the macroscopic analog of the quantization of angular momentum in an atomic system, the fluxoid associated with each hole in the multiply connected superconductor should be quantized to be an integer multiple of the flux quantum (Φ₀ ≒ 2 × 10⁻¹⁵ Wb). Taking advantage of this property, we can tune the magnetic field strength so that the amount of magnetic flux that penetrates the qubit loop is nearly 0.5Φ₀. Then, a clockwise or counterclockwise supercurrent flows on the surface of the loop, making the fluxoid be 0 or Φ₀, respectively. In general, a linear combination of these states will be the energy eigenstate of the system, so we can use these states as a quantum two-level system (qubit).

3. Cavity QED

In order to study the entangled state of atom and light at the single photon level, we first prepare a small cavity resonator to reduce spontaneous emission by decreasing the number of electromagnetic modes to effectively only one that interacts with the atom inside the cavity. By using an extremely high-Q cavity and keeping it at a very low temperature, we can reduce the number of photons inside the cavity to as small as 1 or 0.

Let us consider the two-level approximated atom interacting with a single electromagnetic mode in the cavity shown in Fig. 2. We assume that the electromagnetic field is quantized in the cavity and that the number of electromagnetic modes that interact with the atom is only one. In this condition, the interaction between atom and electromagnetic field can be described by the well-known Jaynes-Cummings Hamiltonian. Here, the first term of the Hamiltonian describes the energy of the two-level atom, the second term is the energy of the electromagnetic field (the constant zero-point energy has been omitted), and the third term is the interaction between atom and electromagnetic field. The vacuum Rabi oscillation, which is the oscillation of the entanglement between atom and photon, can be observed only when the strong coupling condition is established. In other words, the quantum oscillation caused by the interaction can be observed only when the coupling (g) between atom and electromagnetic field is stronger than the photon loss (κ) from the cavity, the spontaneous emission rate (γ), and the inverse transit time of the atom through the cavity (t⁻¹_transit), i.e., g >>κ, γ , t⁻¹_transit.

Fig. 2. Two-level atom interacting with a photon in a single-mode cavity and Jaynes-Cummings Hamiltonian.

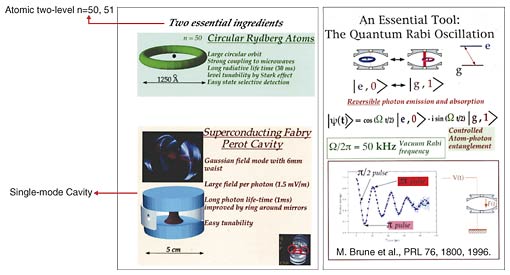
A beautiful experiment performed by Haroche's group in ENS Paris is well known as a representative example of atomic cavity-QED [6]. As shown in Fig. 3, they used two levels of the Rydberg atom state of rubidium (principal quantum number n=50 : |g>, 51 : |e>). Using a very-high-Q (Q ˜−10⁸) superconducting cavity with the system cooled down to 0.3 K, they prepared a strong coupling condition. Finally, they succeeded in observing the quantum entanglement (vacuum Rabi) oscillation.

Fig. 3. Cavity-QED experiment in the atomic system [6].

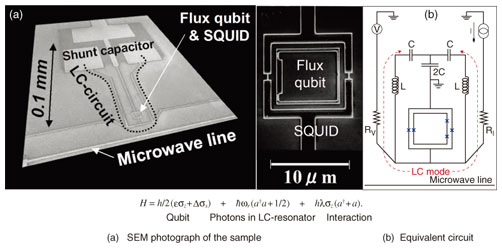
4. Circuit QED with superconducting qubits

The superconducting flux qubit and LC-resonator system that we used in our experiment is shown in Fig. 4. The qubit and LC-resonator were made from aluminum. The LC-resonator was placed around the qubit and its detector SQUID (superconducting quantum interference device). The typical distance between qubit and LC-resonator was a few tens of micrometers. The on-chip capacitance was designed to be C = 10 pF and the aluminum line inductance was designed to be L = 140 pH. The equivalent circuit is shown in Fig. 4(b).

Fig. 4. Superconducting flux-qubit LC-resonator system.

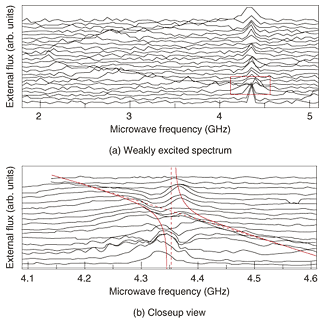
The measured spectrum of the sample is shown in Fig. 5(a). The SQUID switching probability was measured as a function of irradiated microwave frequency as the magnetic flux penetrating the qubit loop was changed. The qubit dispersion had a hyperbolic shape and the peak did not move as a function of applied magnetic field. This range of peaks corresponds to the LC-resonance, and the resonance frequency was in good agreement with the designed value. The resonance frequency of 4.35 GHz corresponds to a temperature of about 200 mK, so at the measurement temperature of around 20 mK in the dilution refrigerator, we could neglect the thermal excitation of the LC-mode. Therefore, we can assume that the LC-resonator was in its ground (vacuum) state with a good approximation. Near the resonance condition of the qubit and the LC-resonator, a 0.1-GHz-order anti-crossing gap was observed, as shown in Fig. 5(b). This is clear evidence of the strong coupling condition inherent in this system.

Fig. 5. Spectrum of the qubit LC-resonator system.

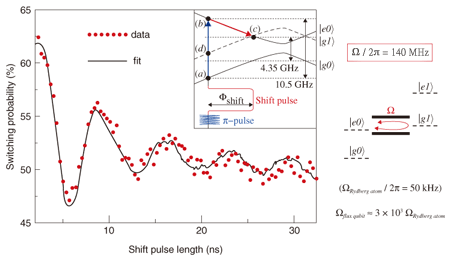
In order to observe dynamical entanglement oscillation, we performed the following experimental procedure. First, we prepared a qubit in its excited state by applying a π-pulse to the qubit in the optimal readout bias condition (inset of Fig. 6 (a)–(b)). Then, we quickly brought the qubit into resonance with the LC-resonator (4.35 GHz) by applying a nanosecond-width DC-pulse for flux-shift (Fig. 6 (b)–(c)). As a function of the time taken to keep the system in resonance, the width of the flux-shift DC-pulse, the readout qubit state is shown in Fig. 6 (b) or (d). Thus, we succeeded in observing temporal quantum oscillation due to entanglement between |e, 0> ⇔ |g, 1> [7]. This phenomenon is called “vacuum Rabi oscillation” because the electromagnetic field is the vacuum field when the qubit is in the excited state.

Fig. 6. Vacuum Rabi oscillation and schematic energy level diagram.

The vacuum Rabi frequency, which is a direct measure of coupling energy, reached 140 MHz. This is about 2800 times that of the Rydberg atom (50 kHz). This very strong coupling is the main reason we were able to succeed in observing time-domain vacuum Rabi oscillation, in spite of the very small Q-value (Q ˜− 50) of the LC-resonator in the present sample.

Thus, if we can make use of the superconductivity, the macroscopic quantum phenomenon, it will be rather easy to establish a strong coupling condition, which is indispensable for cavity QED experiments. One promising idea for making the quantum gate where the control qubit and the target qubit are located nonadjacently is the scheme of the so-called quantum information bus, the qu-bus [8], which couples nonadjacent qubits coherently [9], [10]. The vacuum Rabi process observed in the superconducting qubit and single-mode photon resonator system could be an indispensable component of the qu-bus in a quantum computer. From now on, as a very important challenge, we will first try to improve the coherence time of the system and then control the entanglement among multiple qubits by means of the resonator (qu-bus operation).

References

[1]	I. Chiorescu, P. Bertet, K. Semba, Y. Nakamura, C. J. P. M. Harmans, and J. E. Mooij, “Coherent dynamics of a flux qubit coupled to a harmonic oscillator,” Nature, Vol. 431, pp. 159–162, 2004.
[2]	A. Wallraff, D. I. Schuster, A. Blais, L. Frunzio, R.-S. Huang, J. Majer, S. Kumar, S. M. Girvin, and R. J. Schoelkopf, “Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics,” Nature, Vol. 431, pp. 162–167, 2004.
[3]	A. J. Leggett, “Testing the limits of quantum mechanics: motivation, state of play, prospects,” J. Phys. CM 14, R415–451, 2002.
[4]	A. Blais, R.-S. Huang, A. Wallraff, S. M. Girvin, and R. J. Schoelkopf, “Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation,” Phys. Rev. A, Vol. 69, p. 062320, 2004.
[5]	K. Semba, “Single-shot Readout of a Superconducting Flux Qubit,” NTT Technical Journal, Vol. 16, No. 1, pp. 42–45, 2004 (in Japanese).
[6]	M. Brune, F. Schmidt-Kaler, A. Maali, J. Dreyer, E. Hagley, J. M. Raimond, and S. Haroche, “Quantum Rabi Oscillation: A Direct Test of Field Quantization in a Cavity,” Phys. Rev. Lett., Vol. 76, No. 11, pp. 1800–1803, 1996. http://online.kitp.ucsb.edu/online/colloq/haroche1/
[7]	J. Johansson, S. Saito, T. Meno, H. Nakano, M. Ueda, K. Semba, and H. Takayanagi, “Vacuum Rabi Oscillations in a Macroscopic Superconducting Qubit LC Oscillator System,” Phys. Rev. Lett., Vol. 96, p. 127006, 2006.
[8]	T. P. Spiller, K. Nemoto, S. L. Braunstein, W. J. Munro, P. van Loock, and G. J. Milburn, “Quantum computation by communication,” New Journal of Physics, No. 8, No. 30, 2006. http://www.iop.org/EJ/abstract/1367-2630/8/2/030
[9]	Mika A. Sillanpää, Jae I. Park, and Raymond W. Simmonds, “Coherent quantum state storage and transfer between two phase qubits via a resonant cavity,” Nature, Vol. 449, PP. 438–442, 2007.
[10]	J. Majer, J. M. Chow, J. M. Gambetta, Jens Koch, B. R. Johnson, J. A. Schreier, L. Frunzio, D. I. Schuster, A. A. Houck, A. Wallraff, A. Blais, M. H. Devoret, S. M. Girvin, and R. J. Schoelkopf, “Coupling superconducting qubits via a cavity bus,” Nature, Vol. 449, PP. 443–, 2007.

↑ TOP