You need Adobe Reader 7.0 or later in order to read PDF files on this site.
If Adobe Reader is not installed on your computer, click the button below and go to the download site.

Regular Papers

Vol. 8, No. 8, pp. 31–37, Aug. 2010. https://doi.org/10.53829/ntr201008rp1

Direct Actuation of GaAs Membrane Resonator by Scanning Probe

Masao Nagase^†, Kojiro Tamaru, Keiichiro Nonaka,
Shin’ichi Warisawa, Sunao Ishihara,
and Hiroshi Yamaguchi

Abstract

A method for evaluating the mechanical properties of microresonators and nanoresonators with high spatial resolution is described. Mechanical vibration is directly induced into a circular resonator by voltage applied from a conductive microprobe, and the nanometer-order amplitude of the resonator is simultaneously measured by a scanning probe microscopy system. The resonant properties of 200-nm-thick GaAs circular membranes with a diameter of 14–64 µm were measured and the resonant frequencies were found to range from 0.65 to 5.18 MHz. The minimum detectable amplitude was about 1 nm. The amplitude distributions of the fundamental mode and higher modes were successfully observed with nanometer resolution.

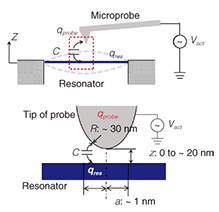
†	University of Tokushima Tokushima-shi, 770-8506 Japan

1. Introduction

Microelectromechanical systems (MEMS) and nanoelectromechanical systems (NEMS) are expected to provide “More than Moore’s Law” devices for future electronics. In MEMS/NEMS, resonant structures are key components for ultralow-mass sensing and single-charge detection [1]–[3]. Optical interferometry and optical deflection techniques, which use laser beams, are standard methods for detecting dynamic mechanical motion with nanometer-order amplitude [4]. However, the spatial resolution of these methods is limited by the diffraction limit of the optical systems. To realize the full potential of MEMS/NEMS, we need to develop a new method for detecting nanometer-order amplitudes with high-spatial resolution. Vibration detection using the microprobe of a scanning probe microscope (SPM) is a promising method for detecting nanovibrations with nanometer-order resolution [5]–[10]. Since the effective contact force in an SPM’s dynamic force mode is small enough compared with the vibration energy of MEMS/NEMS, the resonator’s vibration envelope can be imaged with high-spatial resolution. Vibration detection in various microresonators and nanoresonators, such as single-crystal silicon cantilever devices [5], carbon nanotube beams [6], [7], and graphene membranes [8] has been demonstrated using the SPM-based technique.

The key to improving the SPM-based method is a simple actuation method for microresonators and nanoresonators. In previous studies [5]–[8], additional structures or devices were required to actuate the resonators. One of the most effective and easiest ways to actuate them is to use a piezoelectric actuator [5]. However, the cut-off frequency of the piezo-device is limited by its macroscopic size, so it is not suitable for nanomechanical resonators. Another way is to drive the actuation by the Coulomb force from additional electrodes [6], [7]. However, this method requires complex fabrication processes for the additional electrodes, so it is very difficult to put the electrodes near the target structures. To overcome these problems, we tried to get the SPM microprobe itself to play the role of the actuator in order to eliminate the additional actuating devices. The probe actuates the membrane resonator directly, and nanometer-order amplitudes at megahertz-order frequencies can be detected simultaneously [10].

2. Simultaneous excitation and detection of resonator vibration

In our method, the vibration of the membrane structure is excited by the voltage applied from the conductive probe of the SPM system, as schematically shown in Fig. 1. The minimum distance between the probe and membrane is almost zero because the probe is controlled in the dynamic force mode. Since the Coulomb force strongly depends on the distance, a smaller SPM probe amplitude is preferable for actuation. The typical amplitude in our experiment was about 20 nm. Because the effective probe force is very small, the vibration of the membrane is not affected by observation using the SPM probe. The minimum detectable vibration amplitude of the membrane is about 1 nm.

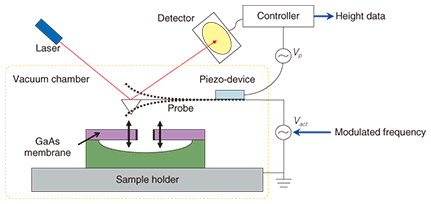
Fig. 1. Schematics of probe and resonator.

The experimental setup of our measurement system is shown in Fig. 2. The sample was simply set in the vacuum chamber of the SPM system (E-sweep from SII-NT). A probe coated with metal (Rh) having a spring constant of 53 N/m was connected to the function generator supplying actuation voltage (V_act) at a modulated frequency. The height information was monitored by the SPM controller (Nanonavi from SII-NT). Since the feedback speed of the SPM controller is very low compared with the vibration of the membrane, we could observe the envelope of the membrane motion. The typical tip radius of the metal-coated probe was about 30 nm, which is suitable for high-spatial resolution observation of a vibrating membrane. All the experiments discussed in this paper were done in vacuum at room temperature.

Fig. 2. Experimental setup.

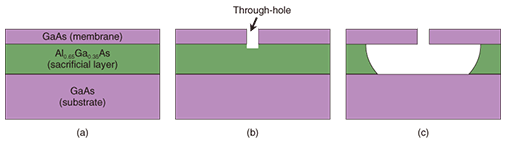
3. Fabrication process of membrane resonator

A 200-nm-thick single-crystal non-doped GaAs epitaxial layer grown on a 1-µm-thick Al_0.65Ga_0.35As layer was used as the membrane resonator in our experiments (Fig. 3(a)). A small through-hole was fabricated in the top GaAs layer by optical lithography with dry etching or focused ion beam (FIB) direct etching (Fig. 3(b)). The Al_0.65Ga_0.35As layer was sacrificially etched using diluted HF solution (Fig. 3(c)). Circular membranes with a diameter ranging from about 10 to 100 µm were obtained by this simple fabrication method.

Fig. 3. Steps in membrane resonator fabrication. (a) Initial structure, (b) through-hole fabrication, and (c) sacrificial etching.

Micrographs of the fabricated membranes are shown in Fig. 4. The membrane with a 65-µm-diameter (a) was fabricated by conventional optical lithography. FIB nano-lithography could fabricate smaller membranes. The 26-µm-diameter membrane with a through-hole with a diameter of about 100 nm was fabricated by FIB etching (b).

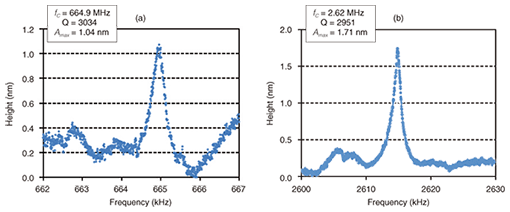
Fig. 4. Micrographs of membranes. (a) Optical micrograph of 65-µm-diameter membrane and (b) scanning electron micrograph of 26-µm-diameter membrane.

4. Experimental results and discussion

4.1 Vibration analyses

Vibration analyses were performed near the center of the GaAs membrane resonator. The vibration characteristics of the membrane resonators are shown in Fig. 5. The frequency of the actuation voltage V_act was swept as a function of time, while the vibration amplitude in the z-direction was monitored as height information by the SPM system. Figure 4(a) shows the fundamental mode of the 65-µm-diameter membrane resonator, whose measured resonant frequency was 664.9 kHz and Q factor was 3034. The fundamental mode of the 26-µm-diameter membrane is presented in Fig. 5(b): the resonant frequency was 2.62 MHz and the Q factor was 2951. The actuation voltage in Fig. 5(a) was 60 mV while that in Fig. 5(b) was 300 mV. Thus, we could successfully detect and actuate vibration of the resonator using the SPM probe.

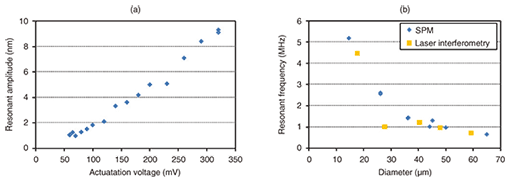
Fig. 5. Vibration analyses for (a) 65- and (b) 26-µm-diameter membranes.

Figure 6(a) shows the relationship between the resonant amplitude and actuation voltage of the 65-µm-diameter resonator shown in Fig. 4(a). The resonant amplitude increased linearly with increasing actuation voltage. Figure 6(b) shows plots of resonant frequencies versus membrane resonator diameter measured by the SPM method (diamonds) and laser interferometry (squares). The SPM-measured frequencies were almost the same as the interferometry-measured ones. The GaAs membrane resonators vibrated at the same frequency as that of the actuation voltage. These results for amplitude and frequency suggest that the Coulomb force between the metal probe and the semiconductor membrane plays an important role in exciting the vibration.

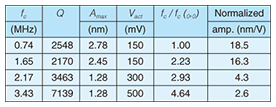
Fig. 6. Resonant characteristics. (a) Actuation voltage dependence of resonant amplitude and (b) relationship between resonant frequencies and diameters.

If a membrane is metal, then the exciting force generated by applying voltage V_act is the electrostatic force F_el , where F_el and V_act are linked by the relation F_el ∝ V_act² [11]. If the mechanical quality factor Q is constant, the resonant amplitude A_max is proportional to F_el. Consequently, in the electrostatic force model for the metal membrane, A_max should be proportional to V_act². Moreover, the frequency of F_el should be twice the driving frequency of V_act. However, for a semiconductor membrane, such as non-doped GaAs, an electrostatic force cannot be generated because carriers in the semiconductor cannot respond to a high-frequency electric field. Fixed charges in the GaAs layer, which originate from residual impurities or the surface state in molecular beam epitaxy growth [12], [13], play a significant role. The Coulomb force F_c is generated between an oscillating voltage V_act applied from the probe and fixed charges in the semiconductor membrane. In the Coulomb force model, the resonant amplitude A_max is proportional to F_c. Therefore, A_max should have a linear relationship with V_act. Furthermore, the force frequency of fc should be equal to the driving frequency of V_act. The experimental results shown in Fig. 5 agree well with the Coulomb force model.

4.2 Higher-order vibration

The resonant frequency of a circular membrane resonator is given by the following formula [14].

where λ_mn is the vibration constant determined by the vibrational mode, h is the membrane thickness, d is the membrane diameter, ν is Poisson’s ratio, E is Young’s modulus, and ρ is the material density. The ratios of higher-order modes to the fundamental mode (f_mn/f₀₀) are 2.08, 3.42, and 4.64 in decreasing order.

The resonant properties of the measured fundamental and higher-order modes of the GaAs membrane resonator with dimensions d=65 µm and h=200 nm are listed in Table 1. The resonant frequency range of this membrane was from 0.74 to 3.43 MHz. The ratios of the higher-order modes to the fundamental mode were 2.23, 2.93, and 4.64. These deviations of the measured ratios from the described theoretical values are attributed to the effects of holes or strain [15].

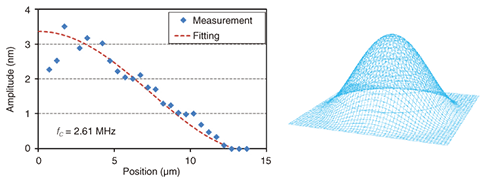
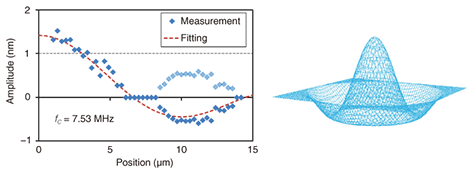
Table 1. Resonant properties of fundamental/higher-order modes of the 65-μm-diameter GaAs membrane resonator.

The normalized amplitude, which is defined by A_max/V_act, decreased with increasing frequency of the higher-order modes. Higher-mode vibrations are difficult to excite because of their larger effective spring constant. At this point, the maximum applied voltage V_act, which is 10 V, is a limiting factor for high-order mode excitation and detection. The maximum measurable frequency of the fundamental mode is also limited to about 10 MHz. More efficient exciting conditions and lower-noise detection techniques will improve the measurable limit of vibration. Note that there is no limitation on the actuation frequency in this method, unlike in conventional optical methods such as laser interferometry. A smaller, thinner membrane, such as a graphene nanomembrane [16], will be suitable for this SPM-based method.

4.3 Mapping of waveform distribution

Since an SPM has nanometer-order spatial resolution, we expect our method to enable the mapping of the waveform distribution of nanoresonators [7]. The displacement distribution will improve our understanding of the mechanical properties of nanoresonators.

Figures 7 and 8 show amplitude distributions of the fundamental mode and a higher-mode of the 26-µm-diameter membrane shown in Fig. 4(b). Dotted lines are calculated waveforms for a circular membrane. The actuation voltage V_act was kept constant for each measured point. Good agreement between the measured and calculated amplitude distributions is important for future applications, such as Young’s modulus determination and accurate calibration of mass, force, and charge sensing.

Fig. 7. Amplitude distribution of fundamental mode.

Fig. 8. Amplitude distribution of higher mode.

For a tapping force of 5 nN and tip radius of 30 nm, the probe-sample contact radius was estimated to be about 1 nm [17], which is much smaller than the spot size of optical systems. This means that the present method has the potential to determine the mechanical properties of much smaller areas than conventional methods. A more detailed investigation will help us understand the effect of very small defects or strain in nanoresonators induced by the fabrication process.

5. Conclusions

We detected nanometer-order amplitudes at megahertz-order frequencies using a vibration analysis method where vibration actuation and detection are performed simultaneously using the probe of an SPM. An accurate vibration analysis can be performed without any probe interaction effect. We have shown that the waveform distribution of the fundamental and higher-order modes can offer a new perspective on the effects of nanometer-order mechanical structures, such as defects and strain. Since the experimental setup of our technique is very simple, this SPM-based technique should be a powerful tool for vibration analyses of nanoresonators.

Acknowledgment

We are grateful to Dr. Reo Kometani of the University of Tokyo for his FIB fabrication and helpful discussion. This work was partly supported by Grants-in-Aid for Scientific Research or KAKENHI from the Japan Society for the Promotion of Science (19206016, 19310085, 20246064, and 22310086).

References

[1]	Y. T. Yang, C. Callegari, X. L. Feng, K. L. Ekinci, and M. L. Roukes, “Zeptogram-Scale Nanomechanical Mass Sensing,” Nano Lett., Vol. 6, No. 4, pp. 583–586, 2006.
[2]	B. Ilic, Y. Yang, K. Aubin, R. Reichenbach, S. Krylov, and H. G. Craighead, “Enumeration of DNA Molecules Bound to a Nanomechanical Oscillator,” Nano Lett., Vol. 5, No. 5, pp. 925–929, 2005.
[3]	D. Rugar, R. Budakian, H. J. Mamin, and B. W. Chui, “Single Spin Detection by Magnetic Resonance Force Microscopy,” Nature, Vol. 430, pp. 329–332, 2004.
[4]	J. Yang, T. Ono, and M. Esashi, “Mechanical Behavior of Ultrathin Microcantilever,” Sens. Actuators, A 82, pp. 102–107, 2000.
[5]	B. Ilic, S. Krylov, L. M. Bellan, and H. G. Craighead, “Dynamic Characterization of Nanoelectromechanical Oscillators by Atomic Force Microscopy,” J. Appl. Phys. p. 101, 044308, 2007.
[6]	A. Volodin, D. Buntinx, M. Ahlskog, A. Fonseca, J. B. Nagy, and C. V. Haesendonck, “Coiled Carbon Nanotubes as Self-sensing Mechanical Resonators,” Nano Lett., Vol. 4, No. 9, pp. 1775–1779, 2004.
[7]	D. Garcia-Sanchez, A. San Paulo, M. J. Esplandiu, F. Perez-Murano, L. Forró, A. Aguasca, and A. Bachtold, “Mechanical Detection of Carbon Nanotube Resonator Vibrations,” Phys. Rev. Lett., Vol. 99, No. 8, p. 085501, 2007.
[8]	K. M. Cheng, Z. Weng, D. R. Oliver, D. J. Thomson, and G. E. Bridges, “Microelectromechanical Resonator Characterization Using Noncontact Parametric Electrostatic Excitation and Probing,” J. Microelectromechanical Systems, Vol. 16, No. 5, p. 1054, 2007.
[9]	A. San Paulo, J. P. Black, R. M. White, and J. Bokor, “Detection of Nanomechanical Vibrations by Dynamic Force Microscopy in Higher Cantilever Eigenmodes,” Appl. Phys. Lett., Vol. 91, p. 053116, 2007.
[10]	K. Tamaru, K. Nonaka, M. Nagase, H. Yamaguchi, S. Warisawa, and S. Ishihara, “Direct Actuation of GaAs Membrane with the Microprobe of Scanning Probe Microscopy,” Jpn. J. Appl. Phys. Vol. 48, p. 06FG06, 2009.
[11]	S. Belaidi, P. Girard, and G. Leveque, “Electrostatic Forces Acting on the Tip in Atomic Force Microscopy: Modelization and Comparison with Analytic Expressions,” J. Appl. Phys., Vol. 81, p. 1023, 1997.
[12]	B. Lee, S. S. Bose, M. H. Kim, A. D. Reed, G. E. Stillman, W. I. Wang, L. Vina, and P. C. Colter, “Orientation Dependent Amphoteric Behavior of Group IV Impurities in the Molecular Beam Epitaxial and Vapor Phase Epitaxial Growth of GaAs,” J. Crystal Growth, Vol. 96, No. 1, pp. 27–39, 1989.
[13]	M. D. Pashley, K. W. Haberern, R. M. Feenstra, and P. D. Kirchner, “Different Fermi-level Pinning Behavior on n- and p-type GaAs(001),” Phys. Rev. B, Vol. 48, pp. 4612–4615, 1993.
[14]	E. Hong, S. Trolier-McKinstry, R. Smith, S. V. Krishnaswamy, and C. B. Freidhoff, “Vibration of Micromachined Circular Piezoelectric Diaphragms,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, Vol. 53, No. 4, pp. 697–706, 2006.
[15]	H. Yamaguchi, K. Kato, Y. Nakai, K. Onomitsu, S. Warisawa, and S. Ishihara, “Improved Resonance Characteristics of GaAs Beam Resonators by Epitaxially Induced Strain,” Appl. Phys. Lett., Vol. 92, p. 251913, 2008.
[16]	M. Nagase, H. Hibino, H. Kageshima, and H. Yamaguchi, “Contact Conductance Measurement of Locally Suspended Graphene on SiC,” Appl. Phys. Express, Vol. 3, p. 045101, 2010.
[17]	M. A. Lantz, S. J. O’Shea, and M. E. Welland, “Simultaneous Force and Conduction Measurements in Atomic Force Microscopy,” Phys. Rev. B, Vol. 56, pp. 15345–15352, 1997.

	Masao Nagase Professor, Material Science and Devices, Department of Electrical and Electronic Engineering, Faculty of Engineering, the University of Tokushima. He received the B.E., M.S., and Dr.Eng. degrees in nanometrology for nanodevices from Waseda University, Tokyo, in 1982, 1984, and 1997, respectively. In 1984, he joined the LSI Laboratories of Nippon Telegraph and Telephone Public Corporation (now NTT), where he worked on R&D of fabrication processes for submicrometer VLSIs. In 1996, he moved to NTT Basic Research Laboratories, where he researched fabrication processes for mesoscopic devices, such as single-electron, NEMS, and graphene devices in the Nanostructure Technology Research Group of the Physical Science Laboratory. He moved to the University of Tokushima in 2010. He is a member of the Japan Society of Applied Physics (JSAP).
	Kojiro Tamaru Trainee, Nanostructure Technology Research Group, Physical Science Laboratory, NTT Basic Research Laboratories. He received the B.E. and M.E. degrees from the University of Tokyo in 2007 and 2009, respectively. He joined NTT Basic Research Laboratories in 2009. He received the Young Author’s Award of MNC2008 as the first author of the outstanding paper entitled “Direct Actuation of GaAs Membrane with the Microprobe of Scanning Probe Microscopy”.
	Keiichiro Nonaka Trainee, Nanostructure Technology Research Group, Physical Science Laboratory, NTT Basic Research Laboratories. He received the B.E., M.E., and Dr.Eng. degrees from the University of Tokyo in 2004, 2006, and 2009, respectively. He joined NTT Basic Research Laboratories in 2009.
	Shin’ichi Warisawa Associate Professor, Department of Mechanical Engineering, School of Engineering, the University of Tokyo. He received the B.E., M.E., and Dr.Eng. degrees from the University of Tokyo in 1989, 1991, and 1994, respectively. In 1994, he was appointed an Assistant Professor in the Precision and Intelligence Laboratory at Tokyo Institute of Technology. In 2000, he was appointed a Lecturer in the Department of Engineering Synthesis at the University of Tokyo, where he researched intelligent manufacturing systems, microfabrication, and medical systems. In 2003, he was promoted Associate Professor. In 2010, he is a visiting scientist at the Research Laboratory of Electronics at MIT, USA. His current research field is nanomechanics and nanofabrication for NEMS.
	Sunao Ishihara Professor, Department of Mechanical Engineering, the University of Tokyo. He received the Ph.D. degree in precision engineering in 1992 from the University of Tokyo for his work on synchrotron x-ray lithography. He joined the Electrical Communication Laboratories of Nippon Telegraph and Telephone Public Corporation (now NTT) in 1973 and worked on microstructure and nanostructure fabrication technologies including x-ray lithography. In 1999, he was appointed Director-General of NTT Basic Research Laboratories and directed nanoscience and nanoengineering. He started teaching and researching in the University of Tokyo in 2005.
	Hiroshi Yamaguchi Executive Manager, Leader of the Physical Science Laboratory Group, Nanostructure Technology Research Group, NTT Basic Research Laboratories. He received the B.E. and M.S. degrees in physics and the Ph.D. degree in engineering from Osaka University in 1984, 1986, and 1993, respectively. He joined NTT Basic Research Laboratories in 1986 and engaged in the study of compound semiconductor surfaces using electron diffraction and scanning tunneling microscopy. His current interests are micromechanical and nanomechanical devices using semiconductor heterostructures. He is a member of JSAP and the Physical Society of Japan.

↑ TOP