Reliable and Efficient Photonic Network Architecture Based on a Hierarchical Hypercube Network Topology

1. Introduction

With the penetration of broadband services, data traffic handled over the communication network has kept increasing over the last decade. This trend is causing serious problems, especially in metropolitan area networks (MANs), since data traffic tends to concentrate in urban areas along with the population. Therefore, a MAN must offer a large capacity and scalability to accommodate the explosive growth in traffic. Moreover, it must provide robustness and flexibility since it is a key social infrastructure. To secure the required robustness, the network should have at least three disjoint^*1 paths between every pair of nodes. In metropolitan areas, the network needs to be flexible enough to efficiently accommodate frequent changes in traffic caused, for example, by a data center being opened or closed.

A photonic network based on wavelength division multiplexing (WDM) is expected to meet these requirements. Although network architectures based on the popular ring and multi-ring topologies have been investigated, they do not provide the necessary degree of link redundancy [1], [2]. To secure network robustness, various path protection/restoration systems for photonic networks have been studied [3], [4]. This paper describes a photonic network architecture that can ensure that there are at least three disjoint paths between any arbitrary node pair and hence provide the robustness required for a MAN.

The rest of this paper is organized as follows. Section 2 discusses MAN requirements. Section 3 describes our hypercube photonic network (HC-PN) architecture. Section 4 analyzes the link capacity requirements for the HC-PN and a conventional ring network. Section 5 compares their other characteristics. Section 6 concludes with a brief summary.

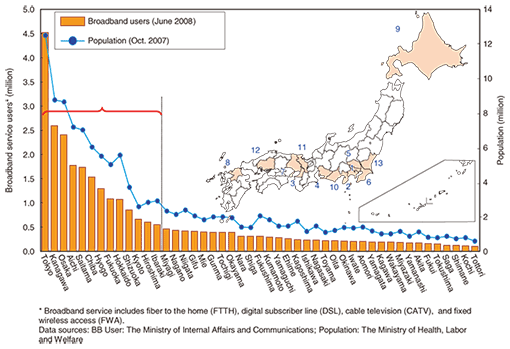
2. MAN requirements

The motivation for this study comes from the fact that the data traffic handled over Japan’s national network is not geographically uniform. The prefecture-by-prefecture distribution of broadband users and population [5] is shown in Fig. 1. The geographical distribution of traffic matches that of broadband users or traffic consumers. The geographical distribution of broadband users corresponds roughly to that of the population. The top five prefectures^*2, where most broadband users reside, are Tokyo, Kanagawa, Osaka, Aichi, and Saitama. 70% of broadband users reside in 13 out of the 47 prefectures (almost 28%). It also shows that 35.4% of broadband users reside in the Tokyo metropolitan area, which includes Tokyo, Kanagawa, Chiba, and Saitama. This suggests that the traffic explosion is an especially serious issue in the Tokyo metropolitan area.

Fig. 1. Broadband user distribution in Japan.

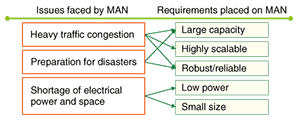
In addition to the traffic explosion, metropolitan areas have unique characteristics that must be considered in designing any future network. The major issues for a metropolitan area, derived from the case of the Tokyo area, are listed in Fig. 2. The first issue is heavy traffic congestion, which is due to the concentration of not only broadband users, who are traffic consumers, but also the traffic generators like Internet exchanges and data centers. The second, which is true for quite a few countries including Japan, is the need to prepare for natural disasters such as earthquakes and typhoons. This is especially important for Tokyo, the capital city. The last one, which is related to the recent worldwide emphasis on protecting the environment, is the shortage of electrical power and space for information and communications technology (ICT) infrastructure because of the concentration of population and economic activities in the metropolitan area.

Fig. 2. Issues for Tokyo metropolitan area network.

We need to take these issues into account in designing a MAN. MAN requirements derived from the above issues are shown in Fig. 3. To handle the heavy traffic congestion, we need a large capacity and good scalability to accommodate the explosive increase in data traffic. MANs must be robust and thus reliable enough to withstand any and all disasters. To handle the shortage of electrical power and space, network equipment must be compact and have low power consumption.

Fig. 3. Requirements for MAN.

Most MANs use ring or star network architectures. These have simple structures and are suitable for collecting the geographically distributed data traffic in a cost-effective manner. However, it is very difficult to satisfy all the requirements listed in Fig. 3 at the same time with these network architectures. A ring-based photonic network using reconfigurable optical add-drop multiplexers (ROADMs) as network nodes has been widely investigated as an approach to developing a low-cost and low-power-dissipation MAN [6]. A photonic ring network is a promising candidate with many attractive features for MANs, but the ring topology provides insufficient robustness against multiple failures. A new architecture that can satisfy all the requirements at the same time is needed.

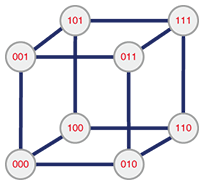
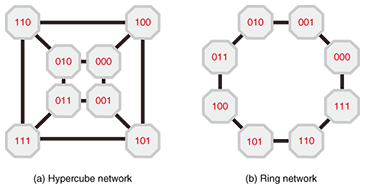
3. Hierarchical hypercube photonic network

We are working on a novel network architecture that can satisfy all the requirements placed on a MAN. It is a photonic network with a layered hypercube network topology (hierarchical HC-PN) and it uses multi-degree ROADMs (MD-ROADMs) as the network nodes [7], [8]. The hypercube network topology and the optical cross-connect (OXC) functionality offered by the MD-ROADM work well together to satisfy the requirements.

The hypercube is well known as one of the most efficient network topologies, especially for interconnection in parallel computers [9], [10]. The configuration of a three-dimensional (3D) hypercube (the familiar cube) network is shown in Fig. 4 as an example. A 3D hypercube has 8 vertices and 12 edges, which correspond to network nodes and links, respectively. We define an n-dimensional hypercube network as follows. It consists of N=2ⁿ nodes, each of which is labeled by a unique binary node number. Nodes whose node numbers differ by only one bit from each other are interconnected by a bidirectional link. As shown in Fig. 4, Node (000) is link-connected to Nodes (001), (010), and (100) since their numbers differ by only one bit from Node (000), in accordance with the definition.

Fig. 4. Configuration of a 3D hypercube network.

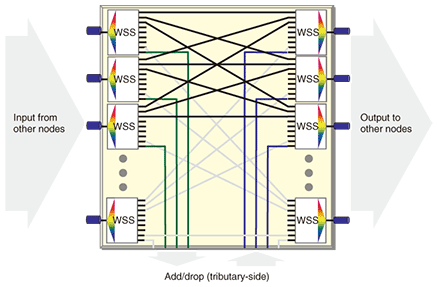
The total number of bidirectional links for an n-dimensional hypercube is (N/2)Log₂N. This characteristic makes the hypercube scalable since the number of links in this network is proportional to O (NLog₂N), which for large-scale networks is much smaller than O (N²), the number of links in a full-mesh network, which is the richest network topology. The hypercube network subsumes lower-order network topologies such as mesh, tree, and ring, and thus exhibits the features of these network topologies. A unique feature of the hypercube with three or more dimensions is that it can form at least three disjoint paths between any arbitrary pair of nodes, which makes the hypercube robust and reliable enough to secure the network against multiple failures. These features make the hypercube network attractive as a MAN solution.

The configuration of an MD-ROADM [11], [12] is shown in Fig. 5. It is composed of wavelength selective switches (WSSs) that are interconnected. A WSS acts as a 1 × N wavelength selective switch. In the switch, each wavelength channel of the input WDM signal can be independently controlled so as to be output from any arbitrary output port. The configuration in Fig. 5 offers add/drop and OXC functions for arbitrary wavelength and input-port signals. An MD-ROADM with more than three input/output ports is now feasible if it is based on WSS devices. It can be used as an OXC that interconnects neighboring network nodes transparently (i.e., without any optical-to-electrical (O/E) or electrical-to-optical (E/O) conversion) or as a building block of the photonic network. The MD-ROADM-based photonic network enables us to handle large-capacity WDM paths without any O/E or E/O conversion, which lowers the network’s cost and power consumption. The HC-PN with MD-ROADM nodes is therefore promising as a MAN.

Fig. 5. Configuration of an MD-ROADM.

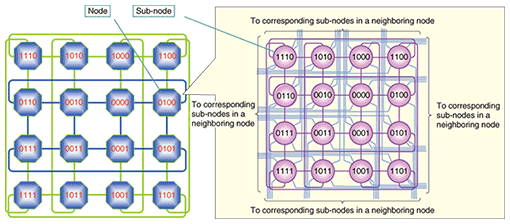
Applying hypercubes to a MAN is much more challenging than applying them to a parallel computer since there are a lot of constraints in designing and constructing a MAN. These include the location of telecommunication buildings, geographical route of installed optical fibers, and geographical distribution of traffic generators and consumers. These factors must be considered as external factors that restrict our freedom in designing the network. To make it easier to install the hypercube network as a real MAN, we have designed a hierarchical hypercube architecture that divides the network into two layers: an inter-building network layer and an intra-building network layer. This hierarchical structure lets us treat the inter-building and intra-building networks independently while retaining the hypercube architecture.

The configuration of a hierarchical HC-PN with MD-ROADM nodes as network nodes is shown in Fig. 6. Here, 16 building nodes form a 4D hypercube network. The links between the building nodes are optical fiber cables. In each building node, 16 sub-nodes (MD-ROADMs) form a 4D hypercube network. Each sub-node has eight input/output ports: four are interconnected to the ports of neighboring sub-nodes in the same building node, and the other four connect to the corresponding sub-nodes in the nodes in neighboring buildings via the optical fiber cables interconnecting the building nodes. The tributary links of each sub-node are connected to the routers of the service network and other client equipment. The configuration in Fig. 6 yields an 8D hypercube network with 256 network nodes. The hierarchical architecture alleviates the network design constraints. The degree of hierarchy can be altered to match the constraints of the network.

Fig. 6. Configuration of an HC-PN using MD-ROADMs as network nodes.

One issue in applying the hypercube network to a practical MAN is the discrete nature of its network scale extension. To extend a 4D hypercube to a 5D one, for example, one must add 16 nodes, so the network cannot be freely extended by any desired number of nodes. This issue can be overcome by introducing the concept of an incomplete hypercube [13], which lets us add network nodes incrementally without sacrificing the advantages of the hypercube architecture.

4. Link capacity requirements

In designing a network, we must assign suitable bandwidth to each link to maximize network efficiency. The link capacity requirements generally depend on both the maximum traffic input from each network node and the network topology. We theoretically investigated the link capacity requirements of the HC-PN and compared them with those of the popular ring-based photonic network. The network topology models used for this link capacity evaluation are shown in Fig. 7. Figs. 7(a) and (b) show a 3D HC-PN with eight network nodes and an eight-node conventional ring network, respectively. In the evaluation, traffic input to the network was assumed to be uniform.

Fig. 7. Network modes for link capacity evaluation. (a) 8-node hypercube network and (b) 8-node conventional ring network.

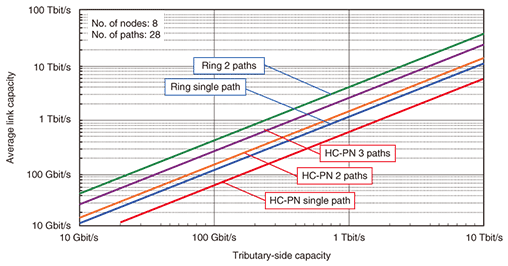
The total bidirectional bandwidth input to the network is expressed as

where b_a and N_n are the bandwidth input from each network node (which we refer to as the tributary-side bandwidth) and the total number of nodes in the network, respectively. The coefficient was set to 0.5 because the traffic was uniform over the network. The total bidirectional bandwidth required for the physical links for node-to-node interconnection is usually larger than B_t in (1) because most bidirectional paths between arbitrary network nodes are multihop paths. In other words, bidirectional paths usually pass over several links to reach their destinations. Taking this into consideration, we derived the required average bandwidth per physical link as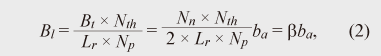

where L_r and N_p are the total number of physical links and the total number of bidirectional paths (equal to N_n(N_n-1)/2), respectively, and N_th is the total number of hops needed to form N_p paths in the network. We define parameter β in Eq. (2) as the ratio of B_l to b_a. It expresses the degree of network complexity. If β is large, say over 10, the network’s physical línk capacity must be, on average, ten times the add/drop (tributary-side) capacity of a node, so the network is intricate and expensive.

The calculated relationship between the tributary-side capacity of a node and the required average link capacity for inter-node connection for both the 3D HC-PN and 8-node ring network is shown in Fig. 8. The horizontal axis shows the tributary-side capacity or the capacity input from a node. The vertical axis shows the average link capacity for inter-node connection. We calculated B_l for three cases where every node-to-node interconnection path was composed of one of the following: a single path, a pair of disjoint paths, or a triplet of disjoint paths. The required link capacity for a ring network is larger than that for an HC-PN because the ring network has a higher total hop number. We note that, of the two network models in Fig. 7, only the hypercube with three or more dimensions offers three disjoint paths for any arbitrary node pair and thus robustness against multiple failures of the network. This is the basis for the HC-PN’s superior robustness.

Fig. 8. Calculated relationship between tributary-side capacity of a node and the required average link capacity.

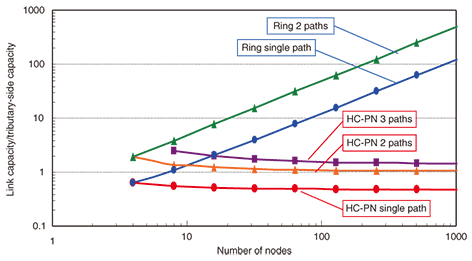
As shown in Fig. 8, in the ring single-path case, the required link capacity is comparable to the tributary-side capacity, i.e., β is nearly equal to 1. However, if two paths are needed to secure network robustness, then the link capacity is four times that for the tributary-side in the case of a ring network. On the other hand, an HC-PN offers two paths, each with link capacity comparable to the tributary-side capacity. Moreover, an HC-PN can provide three disjoint paths while holding the average link capacity to just three times the tributary-side capacity. We therefore conclude that the HC-PN offers scalability and robustness.

Another result of the link capacity analysis is shown in Fig. 9. The graph shows the calculated relationship between the number of nodes and the ratio of link capacity to tributary-side capacity for both a ring network and an HC-PN. The link capacity required for the ring network increases with network scale. On the other hand, the link capacity required for an HC-PN is roughly constant versus the number of nodes, and most values are smaller than 2 for the single-, two-, and three-path cases. These results suggest that the hypercube network will not need link transmission equipment upgrades when it is scaled up.

Fig. 9. Calculated relationship between the number of nodes and the ratio of link capacity to tributary-side capacity.

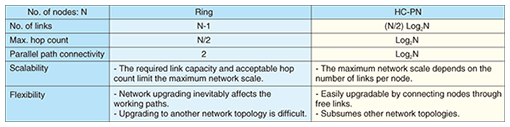
Our study of the link capacity requirements revealed that an HC-PN is superior to a ring network in terms of scalability, upgradeability, and robustness against multiple network failures.

5. Other characteristics

In this section, the other characteristics of an HC-PN are compared with those of a conventional ring network. The results are summarized in Table 1. A ring network does not need as many links as an HC-PN to form a network of the same scale, so its cost is lower. An HC-PN has a lower maximum hop count for path formation than the ring network. This suggests that an HC-PN should have better delay characteristics than the ring network. Only an HC-PN with three or more dimensions can form three disjoint paths, so an HC-PN is robust against multiple failures. The maximum network scale in a ring network is restricted by the achievable link capacity and acceptable hop count, and is usually limited to 10–20 nodes. On the other hand, the maximum network scale of an HC-PN depends on the number of ports per node and can easily be extended to a 100-node network. An HC-PN is easy to upgrade: all that one has to do is to use the free link ports of the nodes to connect additional nodes. This does not affect the working paths, whereas it is impossible to upgrade a ring network without affecting the working paths. Moreover, an HC-PN subsumes other network topologies such as mesh, ring, and tree, which enables it to offer the features of lower-degree topologies. From this network comparison, we conclude that an HC-PN is superior to a ring network in terms of robustness, scalability, and flexibility.

Table 1. Comparison between the conventional ring network and HC-PN.

6. Conclusion

Our novel photonic network architecture based on a hierarchical hypercube architecture (hierarchical HC-PN) and the use of multi-degree ROADMs as network nodes is robust because it offers three or more disjoint paths between each arbitrary node pair if the network’s number of dimensions is three or more. An HC-PN maintains flexibility because the dimensions of the inter- and intra-node networks can be independently set to match the traffic pattern. A link capacity evaluation showed that its link capacity requirement is far lower than that of the popular ring-based photonic network. This feature offers network scalability. Our results suggest that this network is one of the best approaches for handling large traffic volumes efficiently, so it is suitable for overcrowded MANs.

References

[1]	D. W. Jenkins and D. A. Scholtens, “The Transition to Metro WDM Optical Meshes,” Proc. of OFC/NFOEC 2008, Vol. 1, No. 1, pp. 1–10, San Diego, CA, USA, Feb. 2008.
[2]	T. A. Strasser and J. Taylor, “ROADMS Unlock the Edge of the Network,” IEEE Communications Magazine, Vol. 46, No. 7, pp. 146–149, 2008.
[3]	S. Ramamurthy, L. Sahasrabuddhe, and B. Mukherjee, “Survivable WDM Mesh Networks,” J. of Lightwave Technol., Vol. 21, No. 4, pp. 870–883, 2003.
[4]	W. Imajuku, Y. Sone, N. Nagatsu, A. Sahara, and Y. Takigawa, “Highly-reliable and Fast M:N End-to-end Restoration Scheme for Photonic IP Networks,” IEICE Trans. Commun., Vol. E88-B, No. 10, pp. 3914–3921, 2005.
[5]	Ministry of Internal Affairs and Communications (in Japanese). http://www.soumu.go.jp/johotsusintokei/
[6]	Y. Hibino and M. Jinno, “Recent Advances on Node Technologies in Photonic Networks,” Proc. of Photonics in Switching 2007, Vol. 1, No. 1, pp. 33–34, San Francisco, CA, USA, Aug. 2007.
[7]	T. Sakano, A. Kadohata, Y. Sone, A. Watanabe, and M. Jinno, “A Robust and Scalable Photonic Network Architecture Based on a Layered Hypercube Topology,” IEICE Tech. Report, Vol. 109, No. 172, pp. 13–18 (PN2009-13), 2009 (in Japanese).
[8]	T. Sakano, A. Kadohata, Y. Sone, A. Watanabe, and M. Jinno, “Link Capacity Requirements for a ROADM-based Hypercube Photonic Network,” Technical Digest of OECC 2010, Sapporo, Japan, July 2010.
[9]	Y. Saad and M. H. Schultz, “Topological Properties of Hypercubes,” IEEE Trans. on Computers, Vol. 37, No. 7, pp. 867–872, 1988.
[10]	W. D. Hillis, “The Connection Machine,” MIT Press, 1986.
[11]	J. Homa and K. Bala, “ROADM Architectures and Their Enabling WSS Technology,” IEEE Communications Magazine, Vol. 46, No. 7, pp. 150–154, 2008.
[12]	E. B. Basch, R. Egorov, S. Gringeri, and S. Elby, “Architectural Tradeoffs for Reconfigurable Dense Wavelength-division Multiplexing Systems,” IEEE Journal of Selected Topics in Quantum Electronics, Vol. 12, No. 4, pp. 615–626, 2006.
[13]	H. P. Katseff, “Incomplete Hypercubes,” IEEE Trans. on Computers, Vol. 37, No. 5, pp. 604–608, 1988.

↑ TOP