Measurement-based Quantum Computation and the Fault-tolerant System

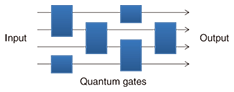
1. Introduction

The principle of current information processing performed by computers and networks is based on the physics of classical electromagnetic dynamics. Information processing technology based on this principle has blossomed in the 20th century as electronics. Meanwhile, a new principle of physics, quantum dynamics, was discovered in the early 20th century for describing the world on the small scale: the scale of the smallest particles and sub-particles. After a while, in the late 20th century, a new principle of information processing based on quantum physics started to be considered. As a result, groundbreaking information processing was found to be possible, such as efficient computation of prime factorization, unconditionally secure communication, and teleportation of quantum information [1]. However, quantum information processing is not easy to realize because the quantum states are difficult to manipulate precisely and are not stable for a long time; i.e., they easily decohere. A lot of study has been going on to achieve the breakthrough needed to realize quantum information processing.

In this article, I review a new computational model for achieving quantum computers called measurement-based quantum computation. Section 2 describes the basic concepts and advantages of measurement-based quantum computation and compares it with the conventional computational model: the circuit model. Section 3 describes an important new fault-tolerant system for quantum computation, topological quantum computing, that can be performed on the basis of the measurement-based quantum computation model in an elegant way. Section 4 describes research on measurement-based quantum computation at NTT laboratories. Section 5 mentions the outlook for future research.

2. Measurement-based quantum computation

From the beginning of the study of quantum computation in around 1990, the realization of quantum computers has been considered on the basis of a standard computational model: the circuit model (Fig. 1). It has a few basic gates such as single-qubit (quantum bit) rotation gates and an important two-qubit interaction gate: the controlled-NOT gate. The input state to the combination of the basic gates achieves universal quantum computation. However, one of the main difficulties in realizing quantum computers is how to make the controlled-NOT gate. It is not easy to obtain an appropriate interaction between particles such as atoms or photons. To date, many experiments toward the controlled-NOT gate have been performed.

Fig. 1. Circuit model.

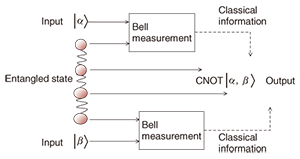
A whole new paradigm for quantum computers started in around 2000. Researchers began to reconsider the computational model in order to utilize the unique features of quantum physics. They thought that there might be a completely different computational model for quantum computers than the one based on the idea of the classical circuit model because the physics is completely different from classical physics. The great feature of quantum states is the existence of entanglement. A breakthrough idea for utilizing entanglement for quantum computers was described by Gottesman and Chuang [2]. They proposed a new model of quantum gates that operate by means of quantum teleportation. Quantum teleportation is a quantum information transmission process that consumes the quantum entanglement in compensation for sending quantum information. We can obtain the output of a controlled-NOT gate by operating quantum teleportation using a special entangled state (Fig. 2). The entangled state can be regarded as a computational resource for the quantum gate.

Fig. 2. Teleportation-based gate.

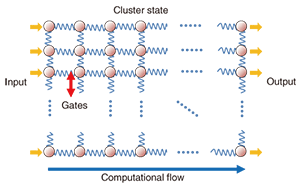
A more sophisticated computational model based on the teleportation-based gate is one-way quantum computation (Fig. 3) [3]. First, a special entangled state, called a cluster state, is prepared beforehand. After that, one only has to perform single-qubit measurement on the cluster state and one can then perform universal quantum computation, in which the entangled cluster state plays the roles of quantum gates and the information flow. The cluster state is a specific entangled state and it can be prepared before computation is started. The entanglement preparation is easier than computation because the target state is known beforehand. Actually, we can even utilize a non-deterministic gate having a low success probability in order to generate the entangled resource [4], [5]. Once the computational resource of the entanglement has been prepared, one only needs to perform single-qubit measurements; this is a very simple task compared with two-qubit interaction gates, so the new computational model significantly decreases the difficulty of realizing quantum computers.

Fig. 3. One-way quantum computation.

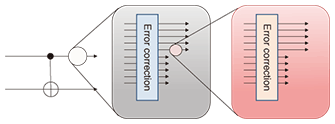
3. Fault-tolerant topological quantum computation

We also need to protect the quantum computing from decoherence and from the effects of several kinds of noise. Fortunately, error correction codes are available for quantum computing and we can perform fault-tolerant quantum computing by applying an error correction procedure appropriately during computation. A well-known fault-tolerant system based on the circuit model used a quantum linear code and concatenated codes (Fig. 4) [6], [7]. A standard quantum linear code encodes a single qubit into several qubits. It can tolerate a single bit-flip and phase-flip error, but if more than one error occurs in the encoded state, then the error correction does not work well. Concatenated coding solves this problem. It recursively uses the linear code as shown in Fig. 4. It provides greater error tolerance if the error rate per basic computational unit is less than a certain threshold. Reliable quantum computing can be executed by using code concatenation of sufficient depth with the error rate below the threshold. The threshold of fault-tolerant systems based on the circuit model is known to be around 1% [7]. However, it is assumed here that any quantum gate can be achieved between widely separated particles, but the interaction between particles normally becomes weaker with increasing distance between particles. Thus, this assumption is unnatural from the physical viewpoint. Though we can rewrite the quantum gate between spatially separate particles into combinations of quantum gates between nearest-neighbor sites, the number of consumed gates becomes larger in that case and the threshold of the fault-tolerant system becomes significantly small.

Fig. 4. Concatenated code.

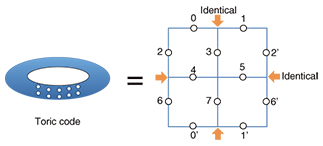
Considering the shortage of concatenated codes for fault-tolerant systems, elegant quantum codes treating physical nearest-neighbor interactions were proposed [8]. They are called topological codes or surface codes; the name originates from the topological nature of the code. The important point is that a topological code uses only nearest-neighbor interactions. This is a realistic scenario compared with the circuit model. An example of a two-dimensional (2D) topological code, toric code, is shown in Fig. 5. The qubits are on the edges of the 2D lattice and entangled as a topological code state. In toric code, the qubits on the endpoints of the 2D lattice are identical to those at the other sides; that is, the 2D lattice is on the surface of a torus, which gives us the degrees of freedom for encoding logical qubits. The entangled code state can be prepared through the use of only nearest-neighbor interactions and the error-checking operations can also be operated by nearest-neighbor interactions and single-site measurements. The encoding size can be enlarged by expanding the lattice size. Toric code can also be rewritten on a square lattice with boundaries by constructing the equivalent for the hole of the torus and introducing the same topology. That makes it easier to prepare multiple logical qubits. Topological fault-tolerant quantum computation is known to be possible in a 2D square lattice with nearest-neighbor interactions during computation, where the obtained noise threshold is 0.75% [9]. Moreover, a special form of 3D cluster state becomes a resource of fault-tolerant topological one-way quantum computation with noise threshold of 0.11% [10]. In this case, we can perform fault-tolerant quantum computing with only single-qubit measurements after preparing the 3D cluster states. The thresholds can be improved by devising better encoding and decoding methods [11], [12]. Recently, the important realistic case of errors with a high loss rate [13] and of non-deterministic entangling gates [14], [15] have also been investigated.

Fig. 5. Topological code.

4. NTT research on measurement-based quantum computation

Here, I briefly describe research on measurement-based quantum computation at NTT Laboratories. In 2008, my colleagues and I experimentally demonstrated a simple scheme for generating a four-photon entangled cluster state and basic operations for one-way quantum computing using the produced state [16]. We showed that the output state fidelities surpass classical bounds, which indicates that the entanglement in the produced state essentially contributes to the quantum operation. However, the obtained fidelities have not been sufficiently high for fault-tolerant quantum computation. In order to perform quantum computing fault-tolerantly, we must improve the gate fidelities experimentally. At the same time, it is important to improve the theory of fault-tolerant quantum computing so that we can utilize realistic imperfect devices. For example, in linear optics, two-qubit gates are intrinsically nondeterministic owing to the linearity of the interaction [4], [17]. In other systems, it is also often the case that a large amount of error such as photon loss and detector inefficiency can be detected in heralded ways, and one can postselect successful events [16], [18]. In 2010, we proposed a scalable way to construct a 3D cluster state for fault-tolerant topological one-way quantum computation using such nondeterministic two-qubit gates with a low success probability [14]. We showed that fault-tolerant topological one-way quantum computation can be performed with a two-qubit gate success probability of less than 1/2 provided that the unheralded error probability of the two-qubit gate is sufficiently small. This work showed for the first time that realistic imperfect nondeterministic gates with a success probability of less than 1/2 can also be utilized for fault-tolerant quantum computing. The other issue in measurement-based quantum computation, reducing the computational resources, is discussed in the second Regular Article [19], which treats a different model of measurement-based quantum computation.

5. Future outlook

Having reviewed the concepts and favorable features of measurement-based quantum computation and the fault-tolerant system, I would like to mention the outlook for future research. On the theoretical side, an important task is to find a more realistic physical model for realizing measurement-based quantum computation. There have been studies for finding Hamiltonians whose ground states are universal resources for measurement-based quantum computation [20], [21]. On the experimental side, some demonstrations of measurement-based quantum computation have been performed [16], [18], [22]. However, a lot of problems remain to be overcome. The most important one is how to obtain scalability in quantum computers. For optical quantum computation, a new high-efficiency single-photon source is necessary [23]. A promising candidate for preparing a large entangled resource for measurement-based quantum computation is ultracold atomic gas in an optical lattice [24]. The important issue for future work on the optical lattice is single-site addressing [25], [26]. Another important candidate is the use of solid-state artificial atoms such as quantum dots or dopants in solids for stationary qubits and the use of atom-photon interactions with cavity quantum electrodynamics for the quantum gates [27]. In conclusion, measurement-based quantum computation provides us with great features toward realizing quantum computers and has high potential for both theoretical and experimental research in the future.

References

[1]	M. A. Nielsen and I. L. Chuang, “Quantum Computation and Quantum Information,” Cambridge University Press, 2000.
[2]	D. Gottesman and I. Chuang, “Demonstrating the Viability of Universal Quantum Computation Using Teleportation and Single-qubit Operations,” Nature, Vol. 402, pp. 390–393, 1999.
[3]	R. Raussendorf and H. J. Briegel, “A One-way Quantum Computer,” Phys. Rev. Lett., Vol. 86, No. 22, pp. 5188–5191, 2001.
[4]	D. E. Browne and T. Rudolph, “Resource-efficient Linear Optical Quantum Computation,” Phys. Rev. Lett., Vol. 95, No. 1, p. 010501, 2005.
[5]	L.-M. Duan and R. Raussendorf, “Efficient Quantum Computation with Probabilistic Quantum Gates,” Phys. Rev. Lett., Vol. 95, No. 8, p. 080503, 2005.
[6]	D. Aharonov and M. Ben-Or, “Fault-tolerant Quantum Computation with Constant Error Rate,” SIAM Journal on Computing, Vol. 38, No. 4, pp. 1207–1282, 2008.
[7]	E. Knill, “Quantum Computing with Realistically Noisy Devices,” Nature, Vol. 434, pp. 39–44, 2005.
[8]	A. Y. Kitaev, “Fault-tolerant Quantum Computation by Anyons,” Annals of Physics, Vol. 303, No. 1, pp. 2–30, 1997.
[9]	R. Raussendorf and J. Harrington, “Fault Tolerant Quantum Computation with High Threshold in Two Dimensions,” Phys. Rev. Lett., Vol. 98, No. 19, p. 190504, 2007.
[10]	R. Raussendorf, J. Harrington, and K. Goyal, “A Fault-tolerant One-way Quantum Computer,” Annals of Physics, Vol. 321, No. 9, pp. 2242–2270, 2005.
[11]	R. Raussendorf, J. Harrington, and K. Goyal, “Topological Fault-tolerance in Cluster State Quantum Computation,” New J. Phys., Vol. 9, 199, 2007.
[12]	D. Wang, A. Fowler, and L. Hollenberg, “Surface Code Quantum Computing with Error Rates over 1%,” Phys. Rev. A, Vol. 83, No. 2, 020302(R), 2011.
[13]	S. Barrett and T. Stace, “Fault Tolerant Quantum Computation with Very High Threshold for Loss Errors,” Phys. Rev. Lett., Vol. 105, No. 20, 200502, 2010.
[14]	K. Fujii and Y. Tokunaga, “Fault-tolerant Topological One-way Quantum Computation with Probabilistic Two-qubit Gates,” Phys. Rev. Lett., Vol. 105, No. 25, 250503, 2010.
[15]	Y. Li, S. Barrett, T. Stace, and S. Benjamin, “Fault Tolerant Quantum Computation with Nondeterministic Gates,” Phys. Rev. Lett., Vol. 105, No. 25, 250502, 2010.
[16]	Y. Tokunaga, S. Kuwashiro, T. Yamamoto, M. Koashi, and N. Imoto, “Generation of High-fidelity Four-photon Cluster State and Quantum-domain Demonstration of One-way Quantum Computing,” Phys. Rev. Lett., Vol. 100, No. 21, 210501, 2008.
[17]	E. Knill, R. Laflamme, and G. Milburn, “A Scheme for Efficient Quantum Computation with Linear Optics,” Nature, Vol. 409, pp. 46–52, 2001.
[18]	P. Walther, K. J. Resch, T. Rudolph, E. Schenck, H. Weinfurter, V. Vedral, M. Aspelmeyer, and A. Zeilinger, “Experimental One-way Quantum Computing,” Nature, Vol. 434, , pp. 169–176, 2005.
[19]	Y. Takahashi, “Reducing the Resources in Measurement-only Quantum Computation,” NTT Technical Review, Vol. 9, No. 7, 2011. https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr201107ra2.html
[20]	T.-C. Wei, I. Affleck, and R. Raussendorf, “Affleck-Kennedy-Lieb-Tasaki State on a Honeycomb Lattice is a Universal Quantum Computational Resource,” Phys. Rev. Lett., Vol. 106, No. 7, 070501, 2011.
[21]	M. Van den Nest, A. Miyake, W. Dur, and H. J. Briegel, “Universal Resources for Measurement-based Quantum Computation,” Phys. Rev. Lett., Vol. 97, No. 15, 150504, 2006.
[22]	W.-B. Gao, A. M. Goebel, C.-Y. Lu, H.-N. Dai, C. Wagenknecht, Q. Zhang, B. Zhao, C.-Z. Peng, Z.-B. Chen, Y.-A. Chen, and J.-W. Pan, “Teleportation-based Realization of an Optical Quantum Two-qubit Entangling Gate,” Proc. of the Natl. Acad. Sci. USA, Vol. 107, pp. 20869–20874, 2010.
[23]	J. L. O’Brien, “Optical Quantum Computing,” Science, Vol. 318, No. 5856, pp. 1567–1570, 2008.
[24]	I. Bloch, “Quantum Coherence and Entanglement with Ultracold Atoms in Optical Lattices,” Nature, Vol. 453, pp. 1016–1022, 2008.
[25]	A. Daley, M. Boyd, J. Ye, and P. Zoller, “Quantum Computing with Alkaline-Earth-Metal Atoms,” Phys. Rev. Lett., Vol. 101, No. 17, 170504, 2008.
[26]	K. Shibata, S. Kato, A. Yamaguchi, S. Uetake, and Y. Takahashi, “A Scalable Quantum Computer with Ultranarrow Optical Transition of Ultracold Neutral Atoms in an Optical Lattice,” Appl. Phys. B, Vol. 97, No. 2, pp. 753–758, 2009.
[27]	T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe, and J. L. O’Brien, “Quantum Computers,” Nature, Vol. 464, pp. 45–53, 2010.

↑ TOP