Speech Dereverberation Using Linear Prediction

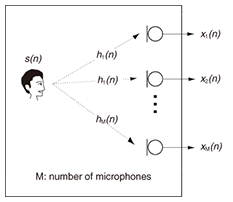
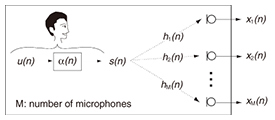
1. Introduction

The last decade has seen the rapid development and pervasiveness of speech technologies, such as hands-free (mobile) telephones, videoconferencing, and hearing aids. In the near future, we can expect to see a dramatic spread of human-machine communication systems, for example, voice-operated electrical appliances and intelligent communication robots, which have already been partially launched and are attracting attention in the market. The main user benefit of hands-free telephones is that they enable the user to walk around freely without wearing a headset or microphone, so they provide a natural communication style. Users of hearing-aid applications obviously benefit from better hearing capability that helps them to interact more fluently with other people. The realization of communication robots will undoubtedly lead to numerous innovative services and technologies, and the benefits brought by these technologies will be literally beyond our imagination.

In all these examples, the position of the target speaker can be at a considerable distance from the microphone. As a result, the observed signal at the microphones can be degraded by reverberation caused by reflection from walls, floors, ceilings, and furniture. The reverberant speech signal recorded at the m-th microphone is generally modeled as: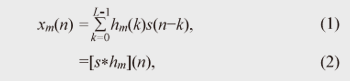

where s(n) denotes clean speech and h_m(n) the room impulse response (RIR) between the source signal and the m-th microphone, which is assumed to be time invariant in this article. [f*g](n) stands for the convolution of f and g. The acoustic system treated in Eq. (1) is shown in Fig. 1. A dereverberation method is generally applied to the received microphone signal x_m(n) to estimate the desired signal s(n). It should be noted that most of the existing acoustic signal processing techniques, e.g., automatic speech recognition (ASR), source separation techniques, and noise reduction techniques [1]–[6], completely fail or experience dramatically reduced performance when reverberation is present. In addition, even after a considerable number of investigations, dereverberation in real environments still remains one of the most challenging speech signal processing tasks to this day. Thus, the investigation of dereverberation algorithms is evidently important.

Fig. 1. Acoustic system treated here.

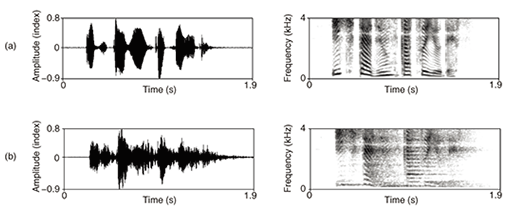
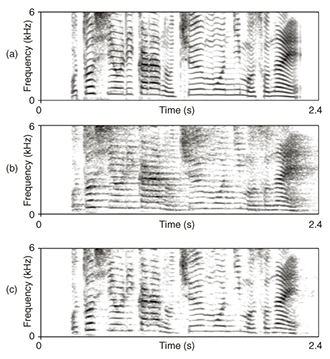
Reverberant speech is generally assumed to consist of three parts: a direct-path response, early reflections, and late reverberation. In this article, the early reflections are defined as the reflection components that arrive after the direct-path response within a time interval of about 30 ms, and the late reverberation as all the latter reflections. Since late reverberation is known to be a major cause of ASR performance degradation and speech intelligibility loss, this article focuses on dealing with the effect of late reverberation. The two most serious detrimental effects caused by late reverberation are summarized below.

(1) Effects on waveform and spectrogram

The effects of late reverberation on speech are clearly visible in the spectrogram and waveform representation. The spectrogram and waveform of an anechoic speech signal are depicted in Fig. 2(a). The phonemes are well separated in time. Now, if the anechoic signal in Fig. 2(a) is reverberated, for instance, with the RIR measured in an office at a distance of 0.5 m from the source, the received signal tends to show the characteristics shown in Fig. 2(b). In Fig. 2, we simulated a situation with RT₆₀ of about 0.6 s, where RT₆₀ is the time required for reflections of a direct sound to decay by 60 dB below the level of the direct sound. The smearing of the phonemes in time is clearly noticeable in both the spectrogram and the waveform. Owing to this smearing, the empty spaces between words and syllables are filled up, and subsequent phonemes overlap [7]–[9]. These distortions result in an audible difference between the anechoic speech and the reverberant speech and lead to degraded speech intelligibility and fidelity. These detrimental perceptual effects are primarily caused by late reverberation, and they generally increase with increasing distance between the source and microphone.

Fig. 2. Waveforms and spectrograms of (a) clean speech signal and (b) reverberant speech signal.

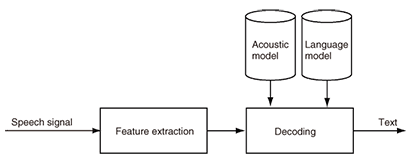
(2) Effect on ASR performance

The performance of ASR systems depends heavily on the quality of the input speech. While reasonable recognition performance is commonly achieved when the source-microphone distance is small, the performance tends to decrease drastically as the distance increases. To explain the reason, we show a block diagram of a typical speech recognition system in Fig. 3. In the system, first, acoustic features such as Mel frequency cepstral coefficients (MFCCs) are extracted from the speech signal using a short time frame (e.g., 30 to 50 ms) of the speech signal. These acoustic features are meant to characterize the essential information present in the speech signal. Next, on the basis of these acoustic features, the most likely text is found by the decoder using two types of knowledge sources: an acoustic model and a language model. The acoustic model contains acoustic knowledge required to decode the features into phonemes, and the language model contains linguistic knowledge required to decode these phonemes into words or sentences. These models should be trained using a set of training data prior to the decoding step. In most cases, the acoustic model is trained on a set of acoustic features extracted from a clean (i.e., undistorted) speech signal. Thus, if the input signal to the ASR system is distorted, for example, by reverberation, the acoustic model mismatches the input signal, which leads to degraded recognition performance.

Fig. 3. Typical ASR system configuration.

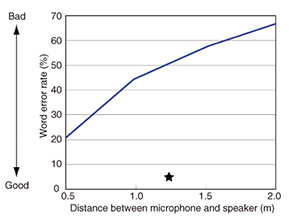
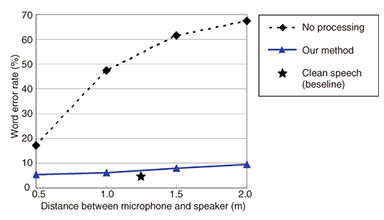
The influence of reverberation on the performance of a state-of-the-art speech recognition system [10], which has been developed at NTT Communication Science Laboratories, is shown in Fig. 4. The word error rate (WER) of continuous speech recognition is shown for various distances in an environment with a reverberation time of 0.6 s. The reverberant signals were generated by convolving anechoic speech signals taken from the Japanese newspaper article speech (JNAS) corpus [11] with a synthetic RIR. The solid line represents the WER for reverberant speech, while the star (★) shows that for clean speech for reference. Note that in this figure, the WER increases with increasing source-microphone distance. From this simple example, it is clear that the effects of reverberation on the ASR system are rather severe. Similar results are obtained if the reverberation time is varied, for example, from 0.1 s to 1.0 s with a fixed microphone-source distance of 1 m.

Fig. 4. Tendency of the WER in a reverberant environment. The solid line represents the WER of the reverberant speech, while the star represents that of clean speech.

2. Difficulty of speech dereverberation

The problem of speech dereverberation has been viewed as one of the most difficult tasks in the field of acoustic signal processing research. To explain the difficulty of speech dereverberation, we show the process of reverberant speech generation in Fig. 5. As you can see from the figure, first, the clean speech signal s(n) is generated as a convolution of white noise u(n) and the impulse response of the vocal tract filterα(n), i.e., s(n)=[u*α](n), and then the reverberant speech x_m(n) is generated according to Eq. (2). That is, the observed signal x_m(n) can be alternatively formulated as

To recover the clean speech s(n) with the observation of only x_m(n), it is necessary to distinguish two unknown impulse responses contained in the observed signal, i.e., α(n) and h_m(n), and remove only the effect due to h_m(n). Since it is not trivial to distinguish these two unknown impulse responses on the basis of only the observed signal, speech dereverberation problem has remained as unsolved problem for many years.

Fig. 5. Process of clean speech and reverberant speech generation.

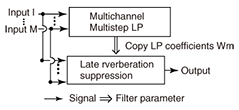
Some researchers have proposed a subspace method for estimating the RIRs by distinguishing these two unknown impulse responses [12]. This method can work effectively in the case of a well-conditioned problem, where the order of the RIR is small and its inverse filter can be calculated in a numerically stable manner. However, real reverberant environments are generally regarded as ill-conditioned problems, where the RIR order is more than several thousand milliseconds, and the calculation of its inverse filter often becomes numerically unstable. Therefore, the subspace method could not work effectively with real recordings. In this article, we propose a dereverberation algorithm that can appropriately distinguish the abovementioned two unknown impulse responses even in the case of an ill-conditioned problem. Thus, it is suitable for speech dereverberation.

3. Dereverberation based on multichannel linear prediction

It is known that linear prediction algorithms [13] are very powerful for estimating the inverse filter of the unknown system. One advantage of using linear prediction is that it is very robust in the case of ill-conditioned problems. However, the conventional linear prediction algorithm does not have mechanism for distinguishing two unknown impulse responses included in the observation process, so it cannot be used for the speech dereverberation as it is. To make the linear prediction algorithm suitable for speech signal dereverberation, in this section, we introduce a dereverberation algorithm based on the generalized linear prediction algorithm, namely multi-step linear prediction (MSLP) [14].

MSLP is designed to estimate and suppress only late reverberation, appropriately distinguishing it from the vocal tract filter α(n). Importantly, the length of the vocal tract filter α(n) is, in general, relatively short compared with that of the RIR h_m(n), such as 30 to 100 ms, while the RIR length can be several hundred milliseconds or sometimes more than a second. By taking advantage of this inherent speech property, i.e., the difference in the lengths of two unknown impulse responses, we can correctly estimate the late reverberation which arrives after the direct path-response with a delay of more than the length of α(n).

First, let us modify Eq. (1) to clearly define the late reverberation component to be estimated with MSLP: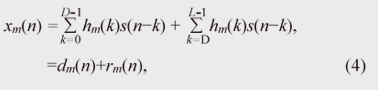

where D is the step-size parameter used in MSLP, d_m(n) denotes the mixture of the direct signal and early reflections, and r_m(n) denotes the late reverberation. Now, if the room transfer function does not share common zeros, it is known that the above equation can be reformulated into the following auto-regressive process using multichannel MSLP: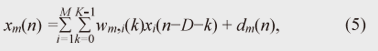

where K is the length of the linear prediction filter, M is the number of microphones, and w_m,i・(n) are the prediction coefficients used to predict the observed signal at the m-th microphone at the present time using the past observed signals at the i-th microphone. As we can see from Eq. (5), the observed signal x_m(n) can be expressed as the addition of the signal components that can be predicted from the past observed signal, and the direct signal plus the early reflections, d_m(n), which cannot be predicted from the past observed signal. Note that, we can also see that, by comparing Eqs. (4) and (5), the first term in Eq. (5) can be regarded as the estimate of the late reverberation component. After estimating the prediction coefficients, we can suppress the late reverberation as in the following inverse filtering form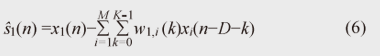

For simplicity, with Eq. (6), we show only the case of suppressing the late reverberation contained in x₁(n).

Needless to say, it is essential to estimate w_m,i(n) as accurately as possible in order to efficiently suppress the late reverberation. In [14], the minimum mean square error criterion is presented for estimating w_m,i(n) as

where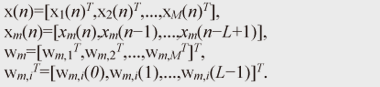

With this estimation scheme, we can show that the linear prediction coefficients for achieving accurate dereverberation can be obtained if step-size parameter D is set as D > T_S, where T_S is defined as

Here, T_S corresponds to the maximum period of time during which the clean speech signal is assumed to maintain a non-negligible autocorrelation value. It should be noted that the clean speech signal is known to have a larger autocorrelation value only within a short-time region due to the characteristics of the vocal tract. In other words, while the short-term correlation of reverberant speech can be affected by both clean speech signal component and early reflection, its long-term correlation is mostly dominated by only the late reverberation effect. Since T_S corresponds roughly to the length of the vocal tract filter α(n) if we set D sufficiently larger than the length of α(n), MSLP can efficiently utilize the long-term correlation as in Eq. (7) and estimate the late reverberation precisely, distinguishing it from the vocal tract filter α(n). With our experiment, we found that the method could estimate an accurate late reverberation component when we used D of 30 ms.

The processing diagram of our dereverberation method based on multichannel MSLP is shown in Fig. 6. First, using multichannel MSLP, we estimate the prediction coefficients for estimating late reverberations at the i-th microphone. Then, on the basis of the estimated coefficients, we perform inverse filtering as in Eq. (6) to achieve the dereverberation. A more robust way of achieving this inverse filtering is presented in [14], and its efficiency has been demonstrated.

Fig. 6. Schematic diagram of our method.

4. Dereverberation experiments

We carried out dereverberation experiments in severely reverberant environments and evaluated the performance of our method in terms of spectrograms and ASR performance.

Spectrograms of clean speech, reverberant speech at a distance of 1.5 m, and speech dereverberated by our method using four microphones are shown in Fig. 7. The effect of the method can be clearly seen. The harmonic structure of the speech signal is well restored, and the separation of the phonemes in time is well reconstructed. The improvement in audible quality can be confirmed in [15]. The WER as a function of the distance between the microphone and speaker is shown in Fig. 8. The dashed line shows the WER of the reverberant speech, and the solid line shows that of the signal processed by our method. The recognition result for clean speech is also plotted by the star (★) as a reference value for the lowest possible WER, i.e., 4.4%, that can be achieved with this ASR system for this recognition task. As seen from the figure, if the reverberant speech is not subjected to any preprocessing, the WER increases greatly with distance. Our method achieved a substantial reduction in the WER for all the tested reverberant conditions.

Fig. 7. Spectrograms of (a) clean speech, (b) reverberant speech, and (c) speech dereverberated by our method using four microphones.

Fig. 8. WER as a function of distance between microphone and speaker.

5. Concluding remarks

A speech signal captured by a distant microphone is smeared by reverberation, which severely degrades the ASR performance and the audible quality of speech signal. In this article, we introduced a novel dereverberation method based on the multichannel linear prediction and showed its efficiency. It can be used, for example, as an efficient preprocessor for ASR system and as a useful speech enhancement tool for audio postproduction engineers [15].

References

[1]	J. Benesty, S. Makino, and J. Chen, “Speech Enhancement,” Springer-Verlag, New York, NY, USA, 2005.
[2]	T. F. Quatieri, “Discrete-time Speech Processing: Principles and Practice,” Prentice Hall, Upper Saddle River, NJ, USA, 1997.
[3]	M. Brandstein and D. Ward, “Microphone Array,” Springer-Verlag, New York, NY, USA, 2001.
[4]	H. L. V. Trees, “Optimum Array Processing,” Wiley-Interscience, New York, NY, USA, 2002.
[5]	S. Haykin, “Adaptive Filter Theory, 3rd ed.,” Upper Saddle River, NJ: Prentice-Hall, 1996.
[6]	S. Haykin ed., “Unsupervised Adaptive Filtering: Blind Source Separation,” Wiley-Interscience, New York, NY, USA, 2000.
[7]	V. O. Knudsen, “The Hearing of Speech in Auditoriums,” J. Acoust. Soc. Am., Vol. 1, No. 1, pp. 56–82, 1929.
[8]	R. H. Bolt and A. D. MacDonald, “Theory of Speech Masking by Reverberation,” J. Acoust. Soc. Am., Vol. 21, No. 6, pp. 577–580, 1949.
[9]	A. K. Nabelek, R. Letowski, and F. M. Tucker, “Reverberant Overlap- and Self-masking in Consonant Identification,” J. Acoust. Soc. Am., Vol. 86, No. 4, pp. 1259–1265, 1989.
[10]	T. Hori, C. Hori, Y. Minami, and A. Nakamura, “Efficient WFST-based One-pass Decoding with On-the-fly Hypothesis Rescoring in Extremely Large Vocabulary Continuous Speech Recognition,” IEEE Trans. Speech, Audio and Language Processing, Vol. 15, No. 4, pp. 1352–1365, 2007.
[11]	“JNAS: Japanese Newspaper Article Sentences,” (in Japanese). http://www.mibel.cs.tsukuba.ac.jp/_090624/jnas/
[12]	S. Gannot and M. Moonen, “Subspace Methods for Multi Microphone Speech Dereverberation,” EURASIP Journal of Applied Signal Process., Vol. 2003, No. 11, pp. 1074–1090, 2003.
[13]	T. Kailath, A. H. Sayed, and B. Hassibi, “Linear Estimation,” Upper Saddle River, NJ: Prentice Hall, 2000.
[14]	K. Kinoshita, M. Delcroix, T. Nakatani, and M. Miyoshi, “Suppression of Late Reverberation Effect on Speech Signal Using Long-term Multiple-step Linear Prediction,” IEEE Trans. Audio, Speech, and Language Processing, Vol. 17, No. 4, pp. 534–545, 2009.
[15]	Sound demonstration of the speech dereverberation software developed on the basis of the principle presented in this article. http://www.tacsystem.com/en/products/softwares/000563.php

↑ TOP