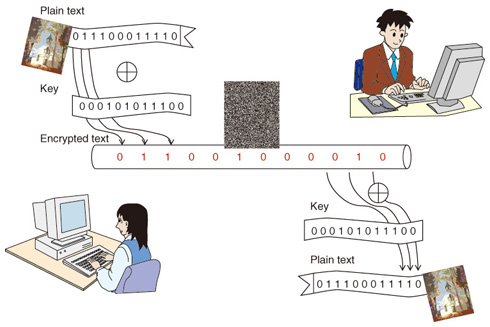
Theory of the Security of Quantum Key Distribution

1.1 Quantum key distribution

Quantum cryptography, especially quantum key distribution (QKD), is a way to securely distribute a secret key to legitimate parties. Here, a key is a table of random numbers shared by legitimate users in such a way that the information is known only to them, and secure means secure against any possible eavesdropping, which is the highest level of security. In this article, we introduce the theory of the security of QKD and say a few words about practical security where we use practical devices.

1.2 One-time pad

What would you think if you received an email from a friend that read "rdlmgvmyroorlmbvm"? At first glance, it does not make sense and looks like a random alphabetic string. You might be worried that your friend's cell phone or personal computer is infected by a computer virus. If you are a good puzzle-solver, however, you would notice that this sentence actually does make sense. Instead of the message being typed directly, this sentence was processed (encrypted) to make it difficult to understand its message. The encryption method used here is uses complementary letters. For instance, to convey Z, you write A; for B, you write Y, and so on. Once you notice this rule, the sentence turns out to be "iwonbillionyen" meaning that your friend won a billion yen and wanted to tell you privately (the message to be conveyed is called plain text). This is a simple example, but it captures the essence of cryptography in the following senses.

The former is the requirement that the sender and receiver communicate faithfully. In our example, the relationship among the words corresponds to this encryption rule, and an encrypted text can easily be decrypted by sharing this rule between the sender and receiver (hereinafter, we call this rule the key). The latter condition refers to the requirement that the communication between the sender and receiver must be secret and must be kept from eavesdroppers. It would be natural to define secure cryptography as a process that ensures an eavesdropper (usually called Eve) will take a long time to decrypt the message. In the case of an encryption method with a fixed key, however, it seems to be impossible to make Eve's decryption time very long. One of the most important points here is that some information, such as email address, header information, receiver's name, time information, etc., has already leaked to potential eavesdroppers in most communications. Thus, Eve can acquire information about the key by using this information together with the encrypted message, and it follows that the more the sender and receiver communicate, the more information about the key is leaked to Eve. Eventually, all the information about the key is known to her.

To resolve this problem, how about changing the key every time we communicate, or even changing the key for each word? This approach does not protect information already known to Eve, but makes the already-known-information useless for obtaining the rest of the key information. This type of encryption method where different encryption methods are used for each message is called a one-time-pad, and it has the strongest security (Fig. 1).

Fig. 1. Cryptographic communication using the key.

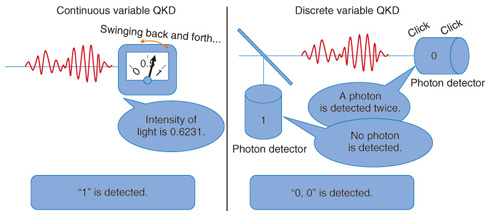
It is very common for usual communications to encode the message into a bit string, so encryption is done by randomly choosing encoding methods where 0 is encoded as 0 (1 is encoded as 1) or where 0 is encoded as 1 (1 is encoded as 0). The former encoding method assigns the bit value 0 in the key, and the latter assigns the bit value 1 in the key. Thus, the key is a random bit string shared by the sender and receiver of the message. The important points for security are that the key length must be the same as the length of the bit string encoding the plain text and that we use each bit of the key only once. Consequently, the one-time pad satisfies the abovementioned condition (1), and as it is impossible for Eve to obtain information that was previously unknown to her, it also satisfies condition (2).

The rest of the question is how to distribute such a key without leakage of its information to Eve? If we want to distribute the key by means of telecommunications, then we have no alternative to using communication channels that are fully accessible to Eve. One assumption that we have to make is that the sender and receiver can authenticate each other (otherwise users might talk with Eve!), which can be achieved by using an authentication protocol, which is a form of classical cryptography. Once secure distribution has been successfully achieved, the one-time-pad becomes a very powerful form of cryptography. But secure key distribution seems to be an impossible task at first glance since Eve seems to be able to obtain all the information flowing over the channels. It turns out that the amount of information about the key that can be extracted by Eve can be made very small by making use of the strange properties possessed by dim light (hereinafter, called a single photon) and of post-selection, and that this asymmetry between Eve and the users in terms of key information does make secure key distribution possible. This key distribution technique is QKD. It is not a way of communicating directly, but a way of sharing the key to be used later to encrypt the plain text.

1.3 Quantum mechanics

In this section, we give a brief explanation of quantum mechanics, which is necessary to understand how QKD works. Roughly speaking, quantum mechanics is a set of principles describing the behavior of very small particles, such as atoms, electrons, and photons. One of the principles tells us that a particle can be in multiple states that are mutually exclusive. For instance, a single particle can exist in many locations simultaneously, which seems very odd to us since we take it for granted that objects normally exist at a single location; a state of this kind is called a superposition state. Another principle in quantum mechanics says that if you observe the location of a particle in the superposition state, then the particle appears in a single location (this principle is called wave function collapse), and it is impossible to deterministically predict where it will appear: we can only determine the probability of the particle appearing at various different locations. Moreover, when more than one particle is in a superposition state at multiple locations, then the superposition states at some locations enhance each other while those at other locations decrease each other. This state behavior is the same as the interference of waves on the surface of water, and just as in the case of the interference of water surface waves, which is mathematically determined by phase, the superposition state also has phase. This property is called the wave character of a particle, and we can say that a particle behaves like a particle as well as like a wave.

One might ask why everyday macroscopic objects do not exist at multiple positions? The answer is that such a relatively big object is always under observation: its location is revealed by light incident on it or through collisions with other particles, such as molecules or dust, so it exists at only a single position. Here, we note that it does not matter whether or not anyone actually observes the object's location: what matters is the fact that the incident light or colliding particles/dust in principle contain information about the object's location, and this information is enough to cause the object's wave function to collapse.

2.1 QKD protocol

Now, we are ready for the explanation of how QKD protocol works. In this article, we explain differential phase shift QKD (DPS-QKD), which was proposed by NTT in collaboration with Stanford University. Here, protocol means a sequence of steps, and in the description of the protocol, we usually assume that the devices used by the sender and receiver operate as those mathematical models require. We will come back to the issue of using actual devices later on.

The protocol starts with the generation of a single photon in the superposition state of position 1, position 2, ..., position N. Since the speed of light in a communication channel such as an optical fiber is constant, this position information is equivalently transformed into time-slot information. Furthermore, we encode a random bit string (N-1 bits) of information as N-1 adjacent relative phase differences. More precisely, the bit value 0 (1) is encoded as the relative phase 0 (π).

The receiver performs a measurement that reads out the relative phase differences. This measurement can be implemented by using beam splitters, which are optical components, and a single-photon detector, which can detect a single photon. An important point here is that since the sender sends only a single photon, the detector receives at most one photon, so at most only one out of the N-1 bits of relative information can be read. As we have mentioned, no one, including the sender and receiver, can ever predict which relative phase information will be read out. Thus, to share the same bit value, the receiver informs the sender over a conventional communication channel, such as a regular telephone, which relative phase information out of the N-1 bits has been read out. Here, note that the receiver must not report the bit value itself. After the sender keeps only the corresponding phase information, the sender and receiver share an identical bit value, and, after many repetitions of above steps, they can share multiple bit values, which form the key.

2.2 Can one eavesdrop on key information?

Next, we consider whether it is possible for Eve to obtain information about the key. A possible form of eavesdropping is one where Eve conducts the same measurement as the receiver. With this measurement, she can successfully get to know about 1 bit of information. Since the sender sends only a single photon, however, she has no idea about the rest of the bit string information. Thus, she has trouble choosing the remaining N-2 bits of information when she sends a single photon to the receiver. Suppose that she chooses the N-2 bits of information randomly. If the receiver accidentally reads out bit information that Eve knows, then the Eve has been successful. However, since no one can ever have control over which time slot information will be read out, there is always some probability that the receiver will read out N-2 bits of unknown information. Moreover, one bit of information that the receiver accidentally reads out from among the N-2 bits will be different from the sender's bit information with probability of 50% (this error is called the bit error). It follows that many repetitions of such communications makes the occurrence of bit errors very likely, which can be detected with high probability. More precisely, after many repetitions of one photon being sent by the sender and one bit information being received by the receiver, the sender and receiver agree by phone on randomly chosen sample bits among the bit data and check by phone whether they really match. If the bit error rate is below a certain value, then they accept all of the remaining bit data and proceed to data processing to distill the key over a public communication channel; otherwise, they discard all the remaining bit values. This threshold is determined from the theory of QKD, and it has been proven that the sender and receiver can generate a key if the bit error rate is below the threshold, regardless of Eve's eavesdropping strategy. This security does not assume any restrictions on the technologies that Eve may exploit. This highest level of security is called unconditional security.

2.3 Other types of QKD protocol

In this section, we briefly mention other types of QKD protocol. The QKD protocol that we have just described above assumes the use of a single-photon source, which it is known can be replaced by attenuated laser light without sacrificing the security. This kind of QKD protocol is called discrete variable QKD since the measurement outcome is bit information. On the other hand, a strong reference light or the difference in the output powers of the detectors can be used in another type of QKD protocol: continuous variable QKD (Fig. 2). Continuous variable QKD allows us to use efficient detectors that operate at normal temperatures, which is one advantage, but its security analysis is not as advanced as that for discrete variable QKD.

Fig. 2. Comparison of continuous and discrete variable QKDs.

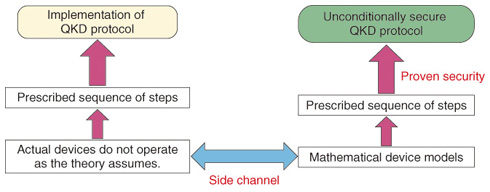
2.4 In what sense is QKD secure?

So far we have had a quick look at QKD. In this section, we would like to mention in what sense QKD is secure. As we have explained above, we can detect Eve's existence probabilistically, not deterministically, and we can never reduce to zero the probability of failing to detect Eve when she is present. For instance, the probability of the receiver detecting the relative phase information that Eve has extracted is very low if the number of detection events is large, but it still cannot be reduced to zero. In this sense, QKD cannot generate a key perfectly.

According to the theory of QKD, however, the probability of the actually generated key showing different properties, such as information leakage, from the perfect key can be made arbitrarily small by the users whatever form of eavesdropping was conducted by Eve. This should be okay since a very small probability should be fine in many communications. For instance, it would be realistic to set this probability to say 10^-6, which means that we would get a single bad event out of a million key generations. In the case of a perfect key with the length of a million bits, this number is , which is an extremely small number and completely negligible. It corresponds to worrying about a single bad outcome in the lifetime of the universe. The fact that users can arbitrarily choose this failure probability is a very good point, and we use this probability to quantify key security in the QKD community.

Finally, we would like to mention the imperfections of users' devices. In our discussion, users' devices were assumed to operate as required for the QKD protocol. However, actual devices do not necessarily operate as required; moreover, they may allow unwanted leakage of information. It is almost impossible to characterize all the details of all devices, so it follows that though such imperfections or unwanted information leakage may be made small through the development of technology or theory, they can never be eliminated. This kind of information leakage due to device imperfections is called a side channel and side channels exist in all types of communications (Fig. 3).

Fig. 3. Differences between protocol and its implementation.

Some recent articles have reported a violation of QKD security, but we must note that this violation was done only by exploiting the side channel: one can never violate the QKD protocol itself. Moreover, the violation of QKD implementation by exploiting the side channel does not compromise the worth of QKD since the QKD protocol is at least unconditionally secure whereas no modern cryptographic protocol is. Therefore, in QKD research, we can concentrate our attention on the side channel. Further research on the QKD side channel is essential to achieve communication that is as secure as possible.

On the other hand, recent QKD systems can handle distances of only 50 km or at most 100 km and the key generation speed still needs to be improved: these are big disadvantages of QKD. Thus, we still need modern cryptography in many situations. Moreover, a side channel exists also in modern cryptography. Thus, collaboration between the QKD and modern-cryptography communities is very important to make the field of cryptography richer.