|
|||||||||||||
|
|
|||||||||||||
|
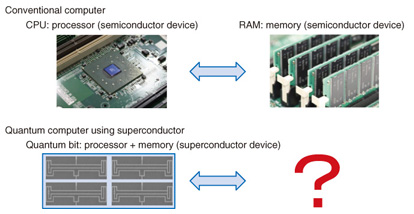
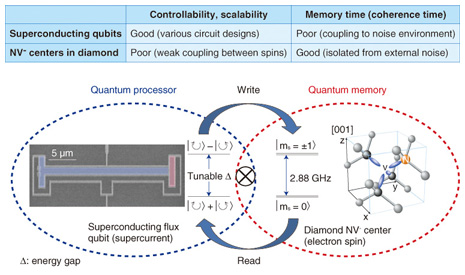
Feature Articles: Quantum Computing Vol. 10, No. 9, pp. 15–21, Sept. 2012. https://doi.org/10.53829/ntr201209fa2 Coherent Coupling between a Superconducting Qubit and a Spin EnsembleAbstractThis article reviews an experiment that demonstrated the principle of quantum memory operation in a superconductor-diamond hybrid system. Superconducting qubits have excellent controllability and scalability but short memory (coherence) time because they are artificial structures; on the other hand, electron spins in diamond are natural structures and have the opposite characteristics: they show extremely long memory times (seconds or greater) but are hard to control and manipulate. A superconductor-diamond hybrid system could offer the best properties of these systems without the associated disadvantages. 1. IntroductionThe coherent control of quantum two-level systems, which are applicable to quantum bits (qubits), has attracted significant interest in the context of quantum computing and quantum information processing. Among the various candidates for quantum bits, superconducting qubits based on Josephson junctions have gained in importance because of their controllability and scalability. Their coherence time has reached a few tens of microseconds [1], compared with several nanoseconds at first in 1999 [2]. A few qubit gates have been demonstrated in superconducting circuits [3]. To execute larger and more useful quantum algorithms in the future though, it will be necessary to achieve a long coherence time. However, we are unsure whether this can be achieved solely with superconducting circuits. The key components of a conventional computer are the central processing unit (CPU) and the random access memory (RAM) (Fig. 1). Each component plays its own unique role. The CPU processes the information while the RAM stores it. On the other hand, superconducting qubits have played the roles of both a processor and memory. In view of the abovementioned issues, NTT has aimed to create a hybrid of superconducting qubits and another suitable system that can store quantum information for longer times [4] (Fig. 2).
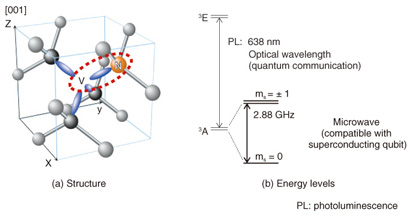
2. NV- centers in diamondNitrogen-vacancy (NV-) centers in diamond have attracted significant attention as a potential candidate for a quantum memory for superconducting qubits. The NV- center is a complex defect in a diamond crystal, formed of (1) a nitrogen (N) atom substituting for a carbon atom and (2) an adjacent vacancy (V) (Fig. 3(a)). As shown in Fig. 3(b), its electron state is spin 1 with a zero field splitting of 2.88 GHz between the ms = 0 and ms = ±1 states at zero magnetic field, where ms is the magnetic quantum number. The electron spin is known for its long room-temperature coherence time of 2 ms [5], so it seems to be suitable for a quantum memory. We can perform a memory operation under low magnetic fields because the zero field splitting of 2.88 GHz is compatible with the transition frequency of superconducting qubits. Furthermore, there is an optical transition in addition to the microwave one, so we may be able to create a quantum transducer––a microwave-to-optical frequency converter. This would be a key technology for quantum repeaters, quantum networks, and quantum computers.
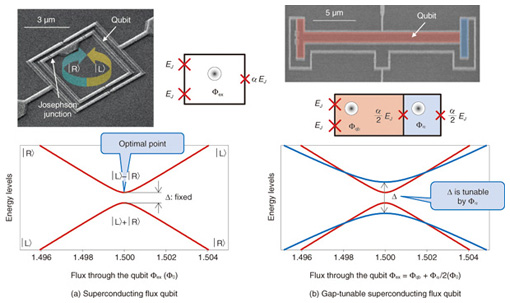
3. Gap-tunable superconducting flux qubitA superconducting flux qubit consists of a superconducting aluminium loop with three Josephson junctions. One of them is α ~ 0.8 times smaller than the other two, which makes its Josephson energy proportionally smaller, i.e., equal to α × EJ (see Fig. 4(a)). The system works as a quantum two-level system, that is, a qubit, when we apply an external magnetic field Φex ~ (m+1/2) Φ0 through the qubit loop (here, m is an integer and Φ0 is the magnetic flux quantum). Figure 4(a) shows the lowest two energy levels of the system when Φex ~ 1.5 Φ0. The clockwise circulating current state |R> and the anticlockwise one |L> are the energy eigenstates when Φex is far away from 1.5 Φ0. These states are composed of persistent currents Ip ~ 300 nA. The equal superposition states between |L> and |R> are realized at the degeneracy point where Φex = 1.5 Φ0 because of tunneling due to the charging energy of the junctions. The tunneling causes energy anticrossing between |L> and |R>, so the transition energy between the ground state and the excited state of the qubit is a minimum at this degeneracy point, which is called the optimal point because it is where the qubit is immune to external flux noise and exhibits its longest coherence time.
We can control the energy gap Δ of the standard flux qubit at this optimal point by an appropriate design of the junction area ratio α; however, we cannot change it after sample fabrication. For our purposes, we need a gap-tunable superconducting flux qubit (Fig. 4(b)) in order to tune our qubit in resonance with other quantum systems, for example, an NV- spin ensemble, while keeping it at the optimal point. We therefore need to replace the smallest junction (α junction) by a dc-superconducting quantum interference device (SQUID), whose EJ can be controlled by the external flux through it. The energy gap Δ can then be tuned in-situ by several gigahertz within a few nanoseconds [6]. The fact that a typical gap is between 1 GHz and 10 GHz thus indicates excellent compatibility with an NV- spin ensemble in diamond. 4. Superconductor-diamond hybrid quantum systemThe coupling strength between two physical systems is the key factor necessary for quantum memory operation in hybrid systems because the time taken to transfer information between the systems is inversely proportional to the coupling strength, so faster operation within its coherence time leads to high-fidelity operation. In the case of the coupling between a flux qubit and the NV- spin ensemble, reducing the spatial distance between them increases the coupling strength because the spin ensemble couples to the qubit through the magnetic field induced by the qubit’s persistent current Ip. Moreover, increasing the density of the NV- spin leads to a stronger coupling because the coupling is enhanced by a factor √N owing to a collective effect when the qubit couples to N electron spins. Therefore, it is important to prepare a diamond crystal that contains a high density of NV- centers. To achieve this, we injected carbon ions into a high-pressure high-temperature (HPHT) synthesized diamond crystal and annealed it in vacuum. We estimated the density of NV- centers to be N ~ 1.1× 1018 cm-3 by comparing the photoluminescence spectroscopy from a single center with that of our ensemble. We fabricated our superconducting flux qubit on a sapphire substrate by using electron beam lithography and a shadow evaporation technique. The diamond crystal was then glued on top of it, achieving a spatial separation of less than 1 µm. The hybrid sample after mounting of the diamond crystal is shown in Fig. 5. We estimated the coupling gi between a single NV- spin and the flux qubit to be approximately 8.8 kHz from the geometrical configuration. This gave the estimated collective coupling gens(estimated) as about 50 MHz for the NV- center density.
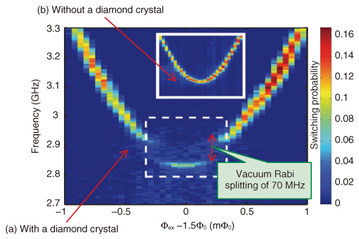
5. SpectroscopyWe performed microwave spectroscopy measurements at 12 mK using a dilution refrigerator. The spectrum of the flux qubit with the diamond crystal shows a clear energy anticrossing at 2.88 GHz (Fig. 6(a)) corresponding to the transition frequency of NV- spins. On the other hand, the spectrum taken before the diamond was mounted (Fig. 6(b)) does not show an anticrossing. From the above results, we can conclude that the splitting at 2.88 GHz comes from the strong coupling gens between the flux qubit and the spin ensemble. The coupling gens of 70 MHz is in good agreement with the coupling gens(estimated) estimated using the NV- center density.
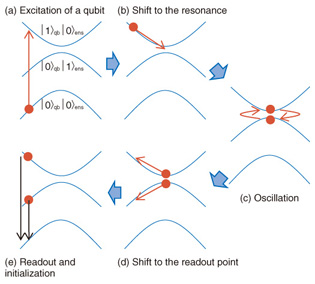
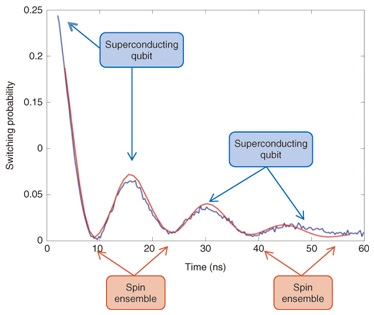
6. Time domain measurementWe performed time domain measurements according to the sequence depicted in Fig. 7 to demonstrate memory operations, that is writing to the spin ensemble and reading from it. First, we excited only the flux qubit by applying a microwave π-pulse to it when the qubit and the spin ensemble were well detuned (Fig. 7(a)). The qubit was quickly tuned by Φex into resonance with the spin ensemble (Fig. 7(b)). This tuning (much faster than the coupling strength gens) causes a non-adiabatic transition, and the flux qubit can then start coherently exchanging a single quantum of energy with the spin ensemble as follows (Fig. 7(c)): |1⟩qb|0⟩ens ⇔ |0⟩qb|1⟩ens , where qb and ens indicate the flux qubit and the spin ensemble, respectively. The 0 (1) represents the ground (excited) state of each part of the hybrid system. The resulting oscillation with frequency gens is called a vacuum Rabi oscillation. Finally, to finish the memory operation, we detuned the qubit non-adiabatically away from the spin ensemble (Fig. 7(d)) and read out the qubit state with a dc-SQUID (Fig. 7(e)). The vacuum Rabi oscillations that we observed are shown in Fig. 8. The blue (red) curve represents experimental data (simulation). These results indicate that quantum information in the flux qubit was transferred to and then retrieved from the spin ensemble.
7. Concluding remarksThe vacuum Rabi oscillations shown in Fig. 8 continued for only 40 ns, which is much shorter than the decay times of the flux qubit (T2,qb ~ 150 ns) and the NV- spin ensemble (T1,NV >> 10 µs). This indicates an unexpectedly short coherence time for the spin ensemble. There are several likely sources of this dephasing. The most probable is a large electron spin – ½ bath derived from the 100 ppm (parts per million) P1 centers (a nitrogen atom substituting for a carbon atom) present in our diamond crystal. The degeneracy of the ms = ±1 states could also be a source of decoherence. Hence, the future challenges are to apply an in-plane magnetic field to remove this degeneracy and to prepare a diamond sample with fewer P1 centers. In summary, we have experimentally demonstrated strong coherent coupling between a flux qubit and a spin ensemble in a diamond crystal. Furthermore, we have observed the coherent exchange (transfer) of a single quantum of energy between them. This is the first step towards a long-lived quantum memory for a superconducting qubit. It could also lead to an interface between the microwave and optical domains. References
|
|||||||||||||