|
|||||
|
|
|||||
|
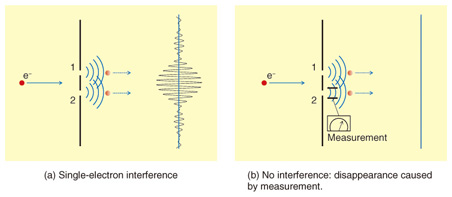
Feature Articles: Quantum Computing Vol. 10, No. 9, pp. 22–27, Sept. 2012. https://doi.org/10.53829/ntr201209fa3 Theoretical and Experimental Study of Quantum Nondemolition Measurement Using an Electric CircuitAbstractWe are investigating, from both the theoretical and experimental standpoints, how to perform measurements on quantum systems by using an electric circuit that has quantum characteristics. A superconducting flux qubit, which is constructed with a superconducting loop circuit, has discrete energy, so it can be regarded as an artificial atom. 1. Superposition state and its measurementIn the quantum world, we can achieve the superposition of several states simultaneously. It is possible to carry out multiple calculations by using a superposition state; therefore, we expect to be able to use it to solve certain types of problems that are difficult to solve with a conventional calculator. An example of a superposition state is shown in Fig. 1(a). A single electron that passes through a double slit exhibits an interference pattern although only one electron reaches the screen because what passes through slits 1 and 2 is a superposition state. If we install an electron detector behind slit 2 to detect which slit the electron passes through, the superposition state disappears and the interference pattern also disappears because the state is decided (Fig. 1(b)).
Similar to this phenomenon, a superposition state is stochastically reduced to a state called an eigenstate by measurement (projection). If the electron is not absorbed by the detector and retains its eigenstate after measurement, this measurement is called a quantum nondemolition measurement. How do we deal with a quantum state measurement that appears strange? We use a superconducting flux qubit as an artificial atom and a Josephson bifurcation amplifier (JBA) readout*1 system, which achieves quantum nondemolition measurement and we study how to perform quantum system measurements both theoretically and experimentally. This study is related to the basic problem of quantum mechanics, namely quantum state measurement. Our goal is to achieve more efficient quantum measurement in the future through an understanding of the mechanism. From a practical point of view, it is important to approach quantum state measurement correctly. Because of the interaction between a qubit and the environment, the qubit coherence, which contains quantum information, gradually decreases. We need quantum error correction to recover this quantum information. We prepare a logical qubit, including an ancillary qubit and a control qubit state that depends on the ancillary qubit’s measured state. In the error correction scheme, our control of the quantum state depends on the result of the ancillary qubit measurement. To make quantum algorithms such as error corrections, it is very important to understand the mechanism of quantum measurement.
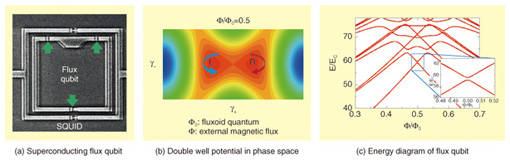
2. Superconducting flux qubitIn a superconducting loop, the phase of a superconducting wave function must be continuous, so only discrete magnetic flux values are allowed. If a Josephson junction*2 is inserted into the loop, a small phase gap is allowed at the junction, so the superconductor phases have time evolution. The energy of a Josephson junction is changed by the junction’s phase. Therefore, the energy of the three Josephson junction loops shown in Fig. 2(a) have a double well potential in the phase space shown in Fig. 2(b). By using the phases at these junctions γ1, γ2, and γ3, owing to the periodic boundary condition of the phases, we can approximately describe γ+ and γ- by γ+=γ1+γ2, γ-=γ3. Because of the charge energy of a junction, phases trapped at two wells denoted L and R can jump between the wells quantum mechanically. This situation is very similar to that of an electron trapped in the nucleus of an atom. As a result, the energy of a superconducting loop also has discrete energy, as shown in Fig. 2(c), and behaves as an artificial atom. A superconducting flux qubit is a two-level system formed of two of the lowest discrete energy levels of a superconducting loop.
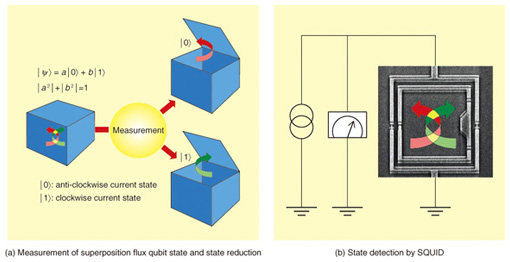
3. Qubit state measurementTwo minimum energy regions in phase space correspond to the clockwise and anti-clockwise supercurrent states of a superconducting loop. Therefore, the supercurrent direction is different for the qubit ground state and the excited state. A quantum superposition state is achieved in a qubit, so we can achieve the superposition of clockwise and anti-clockwise current states. However, this superposition state is stochastically reduced to an eigenstate by measurement, so the detected state is either the clockwise or anti-clockwise current state (Fig. 3(a)). The supercurrent of a superconducting loop generates a small magnetic field. The direction of this magnetic field depends on the superconducting qubit’s quantum state; therefore, by detecting this small magnetic field, we can measure the qubit state. A superconducting quantum interference device (SQUID) is used as a device for measuring small magnetic fields. A small current flows in a SQUID without any voltage (superconducting state); however, voltage does appear when the current exceeds the critical current. The critical current of a SQUID is very sensitive to a magnetic field, so we can detect small changes in magnetic field by detecting the voltage of the current flowing in a SQUID near the critical current (Fig. 3(b)). This method is easy to use, but the superconducting state is destroyed when the SQUID enters the voltage state, so the qubit state is also destroyed. Therefore, we can detect the qubit state, but one more measurement does not reproduce the qubit state. This means that we have no information about the destroyed qubit state. Therefore, we need to develop a new measurement technique that does not destroy the quantum information.
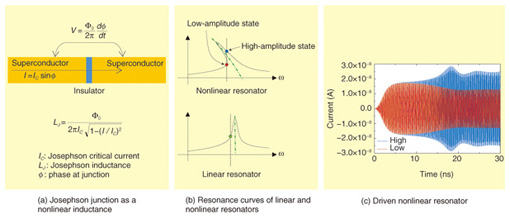
4. Nonlinear bifurcationA Josephson junction works as an inductor in electric circuits, as shown in Fig. 4(a). Unlike a conventional inductor, the Josephson junction exhibits nonlinear characteristics as the applied current is increased. When we drive a nonlinear resonator that includes a Josephson junction, the junction’s inductance increases with increasing driving current. Consequently, the resonance frequency shifts to a lower frequency. When we drive the resonator at a frequency slightly lower than the base resonance frequency, a bistable state appears. One stable state is a low-amplitude state and the other is a high-amplitude state, which is frequency-shifted owing to nonlinearity (Fig. 4(b)). If an external driving current is applied, the resonance state will converge to either the low- or high-amplitude state over time (Fig. 4(c)). The stable state that appears is sensitively dependent on the resonator parameters.
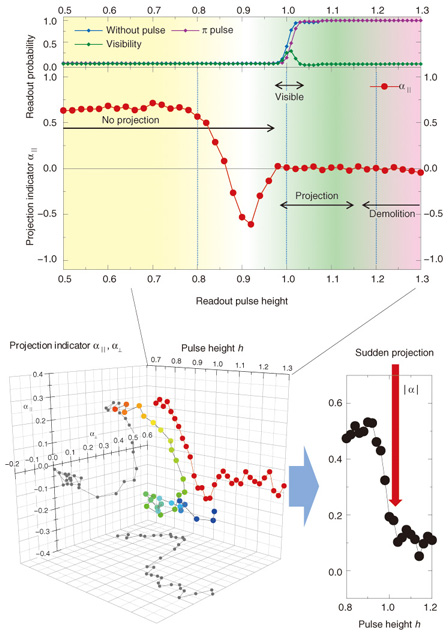
By driving near the bistable state’s boundary, we can detect a small difference in a system that is coupled to a resonator as a difference in the resonator’s resonance state. When we establish a magnetic coupling between a resonator and a superconducting qubit and drive in the optimum microwave condition, we can detect the qubit state by checking whether the JBA resonator is in the high- or low-amplitude state. In this case, the superconducting circuit remains in the superconducting state, so the qubit quantum state is more difficult to break when this readout method is used than when the switching readout method is used. This method is called the JBA readout method. 5. Strength of measurement and projection to eigenstateWith the JBA readout method, we drive a nonlinear resonator with a readout microwave and read the quantum state. How does the projection from a superposition state to an eigenstate occur? We studied when the projection occurred by changing the readout pulse height. First, we prepared a qubit superposition state and applied a short readout pulse. By using a gate operation, we can reproduce the previous state in the case of a superposition state. However, a mixed state after projection generally does not change to the previous state as the result of a gate operation. So we read the qubit state after a gate operation: from the readout pulse, we can know whether or not projection has occurred. To modify the measurement strength, we change the amplitude of the readout pulse and measure it. As a result, the α value, which indicates projection to the eigenstate, suddenly becomes 0 as the readout pulse increases (Fig. 5). This result means that projection does not occur (| α |≠0) when the measurement is weak, and sudden projection (| α |=0) occurs if the measurement strength reaches a critical value.
6. Theoretical analysis of measurementIt is easy to construct a theoretical model of the JBA measurement system for comparison with other systems because a JBA measurement system consists of only a nonlinear resonator and a coupled qubit. We analyzed the JBA measurement system theoretically on the basis of this model. As a result, we confirmed that the superposition state of a qubit interacts with a JBA resonator through an applied readout pulse, and the qubit and JBA resonator form a quantum-entangled state as a result of time evolution. This quantum entangled state achieves the superposition of (1) a qubit ground state and a JBA low-amplitude state and (2) a qubit excited state and a JBA high-amplitude state. Owing to the time evolution of this quantum system, the entangled state is suddenly destroyed by decoherence and is stochastically convergent to one of the two states. These are our predictions for measurement based on theoretical analysis. This measurement analysis corresponds to the sudden projection into the eigenstate that we observed in our experiment when we increased the measurement amplitude, so this phenomenon strongly supports the validity of our theoretical analysis of measurement in a JBA system. 7. Future prospectsOur understanding of how to measure a superconducting flux qubit with the JBA measurement process has progressed. By using this knowledge, we aim to achieve fast measurement and control of quantum states with high accuracy toward the achievement of quantum error correction, which will be essential for quantum computing in the future. |
|||||