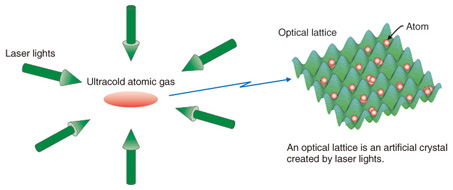
Quantum Simulation with Ultracold Atomic Gases in an Optical Lattice

1. Introduction

In order to explore various properties of matter, we are studying quantum simulation by using ultracold atomic gases at nanokelvin temperatures confined in an optical lattice, which is an artificial crystal created by laser lights. We can introduce our research using the photograph shown in Fig. 1. The green spot at the center indicated by the arrow corresponds to a cold gas of ytterbium atoms emitting fluorescence during laser cooling in the ultrahigh vacuum chamber. This atomic gas is about 1 mm in diameter and contains about ten million ytterbium atoms; the temperature is of the order of 10 μK. An advanced experimental technique based on evaporative cooling has succeeded in further lowering the gas temperature by four orders of magnitude and achieving ultracold atomic gases at temperatures of a few nanokelvins. Such gases are considered to be the coldest matter on earth and they obey laws of physics that are contrary to the common sense that we use in our daily lives, namely they obey quantum mechanics.

Fig. 1. Cold atomic gas of ytterbium confined in an ultrahigh vacuum chamber.

A new approach for studying fundamental problems in quantum mechanics via ultracold atomic gases has recently been attracting many researchers’ interest. One can simulate complicated quantum mechanical phenomena in a well-controlled manner by utilizing the highly controllable atoms available at extremely low temperatures. This approach is therefore referred to as quantum simulation [1].

We know that quantum mechanical effects cause various phenomena found in condensed matter, e.g., the metallic, insulating, magnetic, and superconducting properties of materials. Some of them, however, are highly complicated, so it is still very difficult to obtain a full theoretical understanding of their properties even using supercomputers. A typical example is that the mechanism of high-temperature superconductivity has not yet been completely clarified thirty years after its discovery. We can expect these unresolved problems in condensed matter physics to be solved in the near future through quantum simulation using ultracold atomic gases.

On the other hand, experimental techniques for measuring and manipulating single atoms are showing rapid progress, providing us with promising future applications of atomic gases in quantum technologies. One of the final targets is to construct a quantum computer in which each single atom works as a quantum bit. NTT Basic Research Laboratories has been exploring the enormous potential ability of ultracold atoms both theoretically and experimentally [2].

In this article, we review quantum simulation with ultracold atomic gases and then explain our recent research that has successfully demonstrated the novel quantum state of matter using ytterbium atoms in collaboration with Professor Yoshiro Takahashi’s group at Kyoto University [3].

2. Optical lattice: artificial crystal created by laser lights

An optical lattice is one of the key experimental techniques for quantum simulation based on ultracold atomic gases. We create an optical lattice by applying counterpropagating laser lights to the ultracold cold atomic gas, as schematically depicted in Fig. 2. Here, the laser light wavelength is greatly detuned and is far from the resonance wavelength of the atoms. In this situation, the atoms do not absorb laser photons; hence, heating of the atoms does not occur. The counterpropagating laser lights form a standing wave so as to produce a lattice-like potential that changes periodically with spatial position. An optical lattice corresponds to this periodic potential with atoms confined inside. When laser lights illuminate an atomic gas from six directions, as shown in Fig. 2, the lattice structure becomes a simple cubic one and the lattice distance is exactly equal to half the laser wavelength.

Fig. 2. Schematics of an optical lattice.

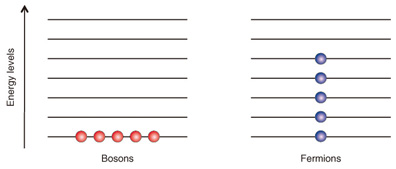
The right diagram in Fig. 2 shows a view of atoms confined on a certain plane in the cubic optical lattice. Atoms move around in the periodic lattice potential by means of quantum tunneling and they interact with each other when multiple atoms coexist at the same lattice site. From this diagram, we understand that an optical lattice acts as an artificial crystal created by laser lights, and confined atoms behave just like electrons in solids. If highly stabilized lasers are used, this optical lattice becomes an ideal crystal without any influence from lattice vibrations, lattice defects, or impurities. Furthermore, the potential depth of an optical lattice changes depending on the laser intensity, which enables the dynamical motion of atoms in this artificial crystal to be controlled via the lasers. Through the development of optical lattices, research on ultracold atomic gases has now become closely related to condensed matter physics.

3. Bosons and fermions

In quantum mechanics, all particles are classified into two kinds of fundamental particles according to their quantum statistics: bosons (bosonic particles) and fermions (fermionic particles). Their energy distributions at the temperature of absolute zero are shown in Fig. 3. Bosons have the property that any number of them can occupy a single energy level. Familiar examples of bosons are photons and helium atoms (mass number: 4). Moreover, superfluidity, which is exhibited by liquid helium at low temperatures, is attributed to the bosonic nature of helium atoms. On the other hand, fermions have a completely different property from bosons: multiple fermions cannot occupy a single energy level. Typical examples of fermions are electrons, protons, and neutrons. Textbooks on condensed matter physics explain many properties of metals and semiconductors on the basis of the fermionic nature of electrons. Furthermore, superconductivity arises from the fact that fermionic electrons form an ensemble of electron pairs and each electron pair behaves as a boson.

Fig. 3. Two different types of quantum-mechanical particle.

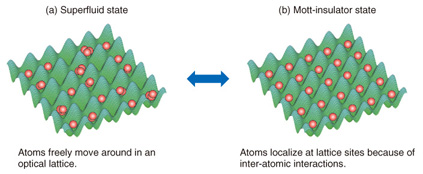
In condensed matter physics, we generally explore the universal features of matter by studying the widest possible range of materials. Quantum simulation via ultracold atomic gases in an optical lattice provides us with a different approach: we investigate universal features directly via artificial model systems created by highly controllable atoms and laser lights that mimic materials. It should be noted here that isotopes play an important role in such quantum simulation. Most atomic species have several stable isotopes containing different numbers of neutrons inside the nucleus. For example, ytterbium has seven stable isotopes: five of them are bosons while the other two are fermions. By using this rich range of isotopes, we can freely choose bosons and/or fermions to investigate. This indicates the great advantage of quantum simulation. Even a single atomic species like ytterbium allows us to investigate various aspects of matter such as superfluids, metals, insulators, superconductors, and magnets.

4. Simulation of quantum phase transitions

Next, we briefly introduce the pioneering work done by the research group at the Max Planck Institute of Quantum Optics in Germany [4], which demonstrated quantum simulation using optical lattices for the first time.

In their experiments, bosonic atoms of rubidium (mass number: 87) were cooled to ultralow temperatures on the nanokelvin order and confined in an optical lattice. As depicted in Fig. 4(a), bosonic atoms stay in the superfluid state at such a low temperature and they can move around freely over all of the lattice sites. However, this situation is limited to the case where the intensity of lattice lasers is low enough and the depth of the optical lattice potential is correspondingly shallow. When the intensity of the lattice lasers is stronger and the optical lattice potential becomes deeper, the interaction between atoms plays a significant role in the quantum states of atoms. In particular, in the case of repulsive interactions where atoms repel each other, bosonic atoms cannot move freely because of the interactions and they are finally localized at lattice sites, as shown in Fig. 4(b). Such localization of bosonic atoms reflects their insulating properties. This insulator state caused by interactions is called a Mott insulator after its theoretical proposer, Sir Nevill Mott.

Fig. 4. Simulation of quantum phase transition from a superfluid to a Mott-insulator.

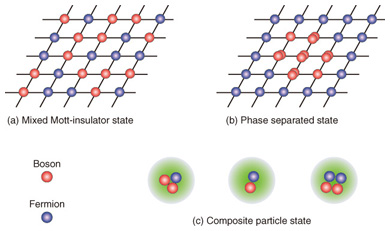
A quantum phase transition (QPT) drastically changes the characteristics of a substance. This phenomenon is caused by many quantum mechanical particles included in the substance such as electrons. QPTs are therefore one of the main research topics in condensed matter physics as a typical example of complicated many-body problems. Figure 4 indicates that, surprisingly, we can simulate the QPT from a superfluid to a Mott-insulator in condensed matter physics by means of ultracold atomic gases confined in optical lattices. Note that the Mott-insulator state is strongly related to the mechanism of high-temperature superconductivity. Similar studies using ultracold fermionic atoms have already been performed mimicking electrons in high-temperature superconductors. On the other hand, as clearly seen in Fig. 4(b), all of the atoms in the Mott-insulator state are strictly ordered in alignment with lattice sites. This sheds light on another promising application of ultracold atoms other than quantum simulation. We should be able to build a scalable quantum computer utilizing every single atom in a lattice as an ideal quantum bit.

5. Recent results: Diverse quantum states achieved in mixtures of bosons and fermions

The diverse properties of substances are closely related to the different characteristics of bosons and fermions, as mentioned above. Perhaps you wonder what kind of quantum states will be achieved by mixing these two fundamental particles—bosons and fermions—in an optical lattice. Of course, such a mixture does not exist in nature. Kyoto University and NTT worked in collaboration to elucidate this unresolved problem [3].

In this collaboration, the research group at Kyoto University performed the experimental studies. Two kinds of atomic gas consisting of bosonic and fermionic ytterbium isotopes were cooled to temperatures of a few nanokelvins and mixed in the optical lattice. All of the experiments were conducted under the condition that the optical lattice was sufficiently deep; hence, both ytterbium gases were in the Mott-insulator regime. This significantly simplified the characteristics of mixtures and made it possible to focus on the influence of interactions between bosons and fermions. The research group at NTT theoretically analyzed the experimental data measured by the Kyoto University group. We used our own calculation method, which corresponds to an extension of the Gutzwiller approximation^* to finite temperatures. We precisely compared the experiments and calculations and clarified that the ytterbium isotopes form the novel quantum states in which bosons and fermions are highly entangled. These states are far from the simple Mott-insulators shown in Fig. 4.

The quantum states of boson-fermion mixtures elucidated by our research collaboration are summarized in Fig. 5. We have studied two cases classified by whether the interaction between bosons and fermions is repulsive or attractive. First, when the interaction is repulsive and the numbers of both particle types are comparable, bosons and fermions repel each other and mix randomly, leading to a random arrangement of single bosons and single fermions at the optical lattice sites, as shown in Fig. 5(a). This state is a completely new quantum state of matter that has been confirmed for the first time in the world; it is referred to as a mixed Mott-insulator. However, when the number of fermions greatly exceeds the number of bosons, both particles are distributed among the optical lattice sites in a spatially separated manner, as shown in Fig. 5(b). We can understand that such a quantum state (i.e., phase separated state) reflects the difference between bosons and fermions depicted in Fig. 3. Bosons tend to occupy lattice sites with multiple bosons at each site, while fermions tend to exhibit single occupancy.

Fig. 5. Diverse quantum states observed in mixtures of bosons and fermions.

Next, when the interaction between bosons and fermions is attractive, the quantum states of the mixtures are completely different to those in the above-mentioned case of repulsive interaction. We have revealed that multiple bosons and fermions combine at lattice sites and form composite particle states, as shown in Fig. 5(c). Interestingly, this composite particle state has different components depending on the numbers of bosons and fermions included in the mixture.

In summary, we have observed diverse quantum states in mixtures of bosons and fermions confined in an optical lattice as a result of the interplay between the characteristics and the interactions of these two different fundamental particles. These quantum simulation results provide us with the important basic concept for one possible origin of diverse phenomena that we generally find in condensed matter systems.

6. Future prospects

Quantum simulation by means of ultracold atomic gases in optical lattices has been making rapid progress in recent years, involving various research fields such as condensed matter physics, quantum information, and quantum chemistry. We are sure that a wide range of research activities seeking both basic studies and future applications is now very important. NTT Basic Research Laboratories is developing quantum technologies for ultracold atomic gases through close mutual cooperation between theoretical and experimental studies. The final aim is to construct a quantum computer based on an optical lattice utilizing single atoms as quantum bits.

References

[1]	I. Bloch, “Ultracold Quantum Gases in Optical Lattices,” Nature Physics, Vol. 1, No. 1, pp. 23–30, 2005.
[2]	T. Mukai, “Making a Quantum Computer Using Neutral Atoms,” NTT Technical Review, Vol. 6, No. 1, 2008. https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr200801sp7.html
[3]	S. Sugawa, K. Inaba, S. Taie, R. Yamazaki, M. Yamashita, and Y. Takahashi, “Interaction and Filling-induced Quantum Phases of Dual Mott Insulators of Bosons and Fermions,” Nature Physics, Vol. 7, No. 8, pp. 642–648, 2011.
[4]	M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch, and I. Bloch, “Quantum Phase Transition from a Superfluid to a Mott Insulator in a Gas of Ultracold Atoms,” Nature, Vol. 415, No. 6867, pp. 39–44, 2002.