Unraveling an Exotic Electronic State for Error-free Quantum Computation

2.1 Non-Abelian quasiparticles

Fundamental particles in nature are classified as either fermions or bosons according to how their wave function changes sign with the interchange of two identical particles. Taking the most familiar examples: electrons are fermions and photons are bosons. Interestingly, the behavior of a system consisting of many particles interacting with each other is often well understood by using the notion of quasiparticles—elementary excitations behaving like particles but with properties different from the parent particles that support the quasiparticle excitations. Examples include holes in a semiconductor and phonons in a crystal lattice. Quasiparticles are also classified according to their behavior upon quasiparticle exchange in terms of whether more than one quasiparticle can be created at the same location. Holes are fermions and phonons are bosons.

Intriguingly, in a two-dimensional space, the statistical properties of quasiparticles are no longer restricted to the fermion/boson dichotomy. For a specific class of quasiparticles termed anyons, the exchange of two quasiparticles adds a complex phase φ to their wave function, through multiplication by a factor e^iφ instead of ±1 for ordinary fermions (-1) or bosons (+1) [20], [21]. The generosity of nature in allowing the existence of such exotic quasiparticles comes as a surprise, but they are not very different from fermions or bosons in that the exchange of these quasiparticles does not alter the state itself. That is, the phase of the wave function acquired after (quasi)particle exchange is factored out by a measurement. Alternatively, it can be said that they are all Abelian, meaning that successive (quasi)particle exchanges in a series are commutative; i.e., the result is independent of the order of (quasi)particle exchanges.

In topological quantum computation, quasiparticles of yet another kind with exceedingly unusual properties are relevant. For these quasiparticles, dubbed non-Abelian quasiparticles or non-Abelian anyons, [11], [12], [22] quasiparticle exchange does alter the state; it transforms the state from one of several degenerate ground states to another. Such an operation can be described by a unitary transformation, so it can form the basis for quantum logic gates. A necessary condition for such quasiparticle exchange to be a nontrivial unitary transformation is that the ground state is degenerate. In the simplest example, a system containing two quasiparticles should have a degeneracy of 2, which then form a qubit. When the system has 2n quasiparticles, there is a 2^n-1-dimensional space of degenerate states, which can be viewed as n − 1 qubits [11]. Table 1 summarizes the classification of (quasi)particles and gives examples of them.

Table 1. Types of (quasi)particles and examples.

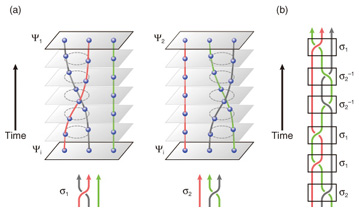
2.2 Topological quantum computation

The ground state of a system containing 2n non-Abelian quasiparticles has a 2^n-1-dimensional space of degenerate states, which serves as n − 1 qubits. Topological quantum computation exploits the unitary transformation of a state that accompanies an exchange of two non-Abelian quasiparticles as a basis for quantum logic gates. The result of the calculation depends solely on the order of the quasiparticle exchanges and does not depend on the details of the quasiparticles’ trajectories. This unique property makes topological quantum computation immune to errors. By using a (2 + 1)-dimensional space-time representation, we can express quasiparticle trajectories as world lines and express quasiparticle exchange as the braiding of two world lines around each other. An example is schematically illustrated in Fig. 1(a). Two of three quasiparticles confined to a two-dimensional plane are manipulated in such a way that they exchange positions via relative motion in the counterclockwise direction. The thick solid lines that trace the position of the quasiparticles in this space-time representation form the quasiparticles’ world lines. The quantum information is encoded in the braid’s topology, that is, the way the world lines are braided. Similar to a braided cord or hair, which can be loosened but not undone, the quantum information is not affected when the quasiparticle trajectories are locally perturbed. The quantum information is thus said to be topologically protected. Fig. 1(b) shows an example of logic gate operations consisting of the basic operations shown in Fig. 1(a) and their inverses.

Fig. 1. Schematic illustrations of quasiparticle exchanges and topological quantum computation. (a) Basic operations (σ₁ and σ₂) on a system containing three quasiparticles. Top: illustrations of the temporal evolution of the system from the initial state ψ_i to the final state ψ₁₍₂₎ = σ₁₍₂₎ψ_i. Bottom: diagrammatic representations of the quasiparticle exchange operations. (b) Example of logic gate operations consisting of the basic operations σ₁ and σ₂ shown in (a) and their inverses σ₁^-1 and σ₂^-1.

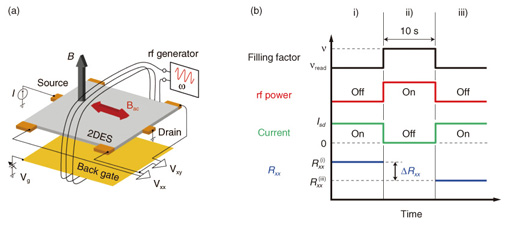
3.1 Quasiparticles in FQH states

A prime candidate for a physical system expected to host non-Abelian quasiparticles is an exotic state of a two-dimensional electron system (2DES), called the ν = 5/2 FQH state [15]. This state emerges in a pristine semiconductor heterostructure under extreme conditions of millikelvin temperature and high magnetic field of several tesla. FQH effects are characterized by the quantization of Hall resistance that occurs when the applied field B and the electron density n take particular ratios [23]. Hall resistance R_xy is usually related to n and B as R_xy = B/ne, where e is the elementary charge. As a consequence of electron-electron interaction, an energy gap forms at the Fermi level for particular values of B/n, around which R_xy is pinned at a constant value over a finite range of n and B [24]. The energy gap also leads to the vanishing of longitudinal resistance R_xx.

Because of the energy gap that forms at particular values of B/n, the electron system tries to preserve the same B/n ratio to minimize the interaction energy when B or n is slightly detuned. The resultant mismatch is accommodated by introducing point defects around which the local electron density is higher or lower than in the surrounding area. These point defects, which carry electric charge and behave like charged particles, are quasiparticles in FQH systems [24]. FQH quasiparticles have been shown to have a fraction of the electron charge [25], [26] and are believed to be anyons [21]. Their properties, including their charge and statistics, are derived from the properties of the FQH state hosting them. The FQH state that emerges at ν = 5/2, where ν = (h/e)n/B (h: Planck’s constant), is believed to have the distinctive property that its quasiparticles are non-Abelian [18].

3.2 Theoretical models for the ν = 5/2 state

The ν = 5/2 FQH state [15], [16] and its particle-hole counterpart ν = 7/2 are the only FQH states with even-denominator ν observed in a single-layer 2DES. Unlike other FQH states with odd-denominator ν, the exact mechanism responsible for the energy gap formation at ν = 5/2 has not yet been established. In the standard theory of FQH effects [24], [27], [28], the fermionic nature of electrons requires ν to have an odd denominator. Thus, the breaking of the odd-denominator rule suggests a paired state of fermions [19], [29]. Various theoretical models have been proposed and examined [18], [19], [29]–[36], including both those with non-Abelian statistics and those with Abelian statistics.

Experiments reported thus far have neither demonstrated the non-Abelian nature of ν = 5/2 quasiparticles nor pinned down precisely which theoretical model correctly describes the ν = 5/2 ground state. The quasiparticle charge of e/4 observed in shot noise [37], [38] and local compressibility [39] measurements indicates that the ν = 5/2 state is indeed a paired state, but does not discriminate among different types of paired states which all have charge-e/4 quasiparticles. Notably, quasiparticle tunneling between FQH edges through a narrow constriction [40], [41] has allowed the screening of different model wave functions through detailed comparison with theory. However, the likely candidates that emerged through these experiments include an undesirable Abelian wave function.

3.3 Spin polarization of the ν = 5/2 state

Most theories of topological quantum computation using the ν = 5/2 state as a platform to manipulate non-Abelian quasiparticles [11], [42] are based on the premise that the state is described by the wave function proposed by Moore and Read [18], which is considered to host non-Abelian quasiparticles. An important feature of the Moore-Read theory is that it assumes that all the electrons have their spins—an internal degree of freedom of electrons making them behave like tiny magnets—aligned along the same direction. Numerical studies have shown that the ground state at ν = 5/2 is spin polarized [43]–[45]. However, experiments reported thus far have indicated conflicting results for the spin polarization of the ν = 5/2 state [46], [47]. The addition of an in-plane magnetic field to increase the spin-splitting energy is known to weaken the ν = 5/2 state [48], [49], which hinted at an unpolarized or only partially polarized state. On the other hand, under a perpendicular magnetic field, the ν = 5/2 state persists over a wide range of magnetic field, even up to 10 T [50], suggesting full polarization. Recent optical measurements using photoluminescence [51] and inelastic light scattering [52] indicated an unpolarized state or an inhomogeneous state consisting of unpolarized or partially polarized domains, respectively. It is therefore of paramount importance to determine the spin polarization with a high level of confidence.

4.1 NMR

NMR spectroscopy is one of the most powerful and sophisticated analytical tools for investigating the electronic and structural properties of matter. It exploits the resonant absorption of electromagnetic waves by nuclei placed in a strong magnetic field. When the electron system surrounding the nuclei has non-zero spin polarization, the hyperfine interaction between the electron spins and the nuclear spins acts as an effective magnetic field for the nuclei: this field shifts the nuclear resonance frequency by a small amount (Knight shift) proportional to the electron spin polarization. Thus, the electron spin polarization can be deduced by measuring the Knight shift of nuclei placed in contact with a 2DES. All three nuclides, ⁶⁹Ga, ⁷¹Ga, ⁷⁵As, constituting the GaAs quantum well, where a 2DES resides, have nuclear spin I = 3/2 and can consequently serve as NMR probes.

The challenge in applying NMR to 2DESs is the low signal level resulting from the small number of nuclei in contact with the 2DES and the overwhelming background coming from the thick substrate. Resistively detected NMR (RD-NMR) [53], [54] provides a way to overcome these issues of sensitivity and selectivity, thereby allowing us to perform NMR on a single sheet of a 2DES. Instead of probing inductive signals via a pickup coil or directly measuring the absorption, in RD-NMR we measure the change in the electrical resistance of the sample that occurs when the frequency of the applied radio-frequency (rf) wave matches the resonance frequency of the nuclei. In return for its high sensitivity, the conventional RD-NMR has the drawback of being applicable only under a particular set of conditions such that the electron system has measurable finite electrical resistance and is sensitive to a tiny change in the electronic Zeeman energy. The former implies that the method is not applicable to a well-developed quantum Hall state, where the sample’s resistance exponentially vanishes at low temperatures; the latter condition is necessary because resistive detection relies on the hyperfine coupling between electron spins and nuclear spins, which acts as an effective magnetic field modifying the electronic Zeeman energy.

4.2 Sample and method

The sample used in our study was a 27-nm-wide GaAs quantum well with Al_0.25Ga_0.75As barriers grown by molecular beam epitaxy. The structure was doped with Si on one side (front) of the quantum well at a setback distance of 90 nm, which provided the 2DES with density n = 1.55 × 10¹¹ cm^-2 and mobility µ = 5.8 × 10⁶ cm²/Vs in the as-grown condition. The sample was processed into a 100-µm-wide Hall-bar device. A degenerately Si-doped GaAs buffer layer 1 µm below the 2DES served as a back gate [55], which allowed us to tune the electron density n over a wide range: from 0.5 × 10¹¹ cm^-2 to 4.2 × 10¹¹ cm^-2. The mobility exceeded 1.0 × 10⁷ cm²/Vs for n ≥ 2.8 × 10¹¹ cm^-2, reaching a maximum value of 1.15 × 10⁷ cm²/Vs at around n = 3.9 × 10¹¹ cm^-2. To observe a well-developed ν = 5/2 state, it is essential to control the disorder potential due to the remote ionized impurities in the Si doping layer. Details of the sample optimization are given in [56].

Our measurement setup is schematically shown in Fig. 2(a). A Hall-bar device mounted on a DIP (dual inline package) chip carrier is cooled in the mixing chamber of a dilution refrigerator with a base temperature of 10 mK. A three-turn coil is wound around the sample and connected to an rf generator. Electrical measurements are performed by driving a low-frequency (17 Hz) ac current I_sd through the sample and measuring the voltages V_xx and V_xy that appear in the longitudinal and transverse directions using lock-in amplifiers. The longitudinal and Hall resistances are obtained as R_xx = V_xx/I_sd and R_xy = V_xy/I_sd.

Fig. 2. (a) Experimental setup and (b) measurement sequence of resistively detected nuclear magnetic resonance.

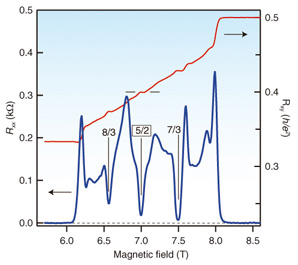
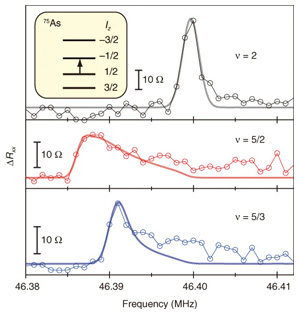
Our measurement sequence consists of three steps, i) to iii), as schematically shown in Fig. 2(b) [17]. The salient feature of our measurement scheme is that we exploit an electronic state (designated by filling factor ν_read) that is different from the electronic state of interest (designated by filling factor ν) to read out the change in R_xx that results from the rf irradiation on the state ν. As shown in Fig. 2(b), this is done by switching the gate voltage V_g at a fixed magnetic field B while alternately turning on and off the current and the rf wave [57]. Our signal is the difference (ΔR_xx = R_xx⁽ⁱ⁾ - R_xx⁽ⁱⁱⁱ⁾) in R_xx measured in periods i) and iii), right before and after the period ii). By repeating this sequence for different frequencies, we obtain a resonance spectrum. It is important to note that, although we measure R_xx of the state ν_read, the spectral information contained in the resultant NMR spectrum reflects only the electronic properties of the state ν. It is also important to note that while the state ν_read needs to satisfy the conditions required for conventional RD-NMR, the state ν does not. This eliminates the restrictions imposed on conventional RD-NMR, allowing RD-NMR to be performed for any electronic state accessible via gate voltage. Specifically, we used ν_read = 0.59; in this range of filling factor, the electronic system is very sensitive to a small change in the Zeeman energy [58], [59]. Below, the filling factor ν refers exclusively to the value during step ii).

4.3 Experimental results

R_xx and R_xy of our sample as a function of magnetic field B are shown in Fig. 3. Fractional quantum Hall effects at Landau-level filling factor ν = 8/3, 5/2, and 7/3 are manifested as plateaus in R_xy and minima in R_xx, indicating high sample quality. The RD-NMR spectra of ⁷⁵As nuclei measured at B = 6.4 T are shown in Fig. 4. As shown in the inset, the magnetic field splits the energy levels of ⁷⁵As nuclear spins I = 3/2 into four levels with I_z = ±3/2 and ±1/2. Here, we focus on the transition between I_z = 1/2 and –1/2. (Other transitions, which are split off by quadrupole interactions, are outside the frequency range shown in the figure.) In Fig. 4, spectra taken at three different filling factors ν = 2, 5/2, and 5/3 are shown. As explained below, the spectra for the ν = 2 and 5/3 states, whose spin polarizations are known, are necessary to deduce the Knight shift at ν = 5/2 and convert it into spin polarization.

Fig. 3. Magnetotransport properties of the sample used for the resistively detected nuclear magnetic resonance measurements.

Fig. 4. Resistively detected nuclear magnetic resonance spectra of ⁷⁵As nuclei taken at B = 6.4 T. The top, middle, and bottom panels show spectra taken at Landau-level filling factor ν = 2, 5/2, and 5/3. The thick solid lines show the fitting based on model calculations. The inset shows the nuclear spin levels.

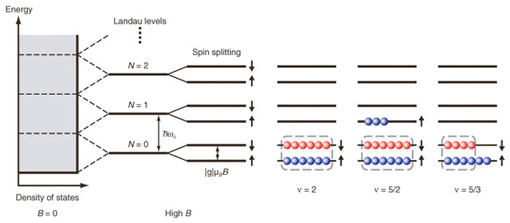
The electron configurations at these filling factors are schematically shown in Fig. 5. When a 2DES is subjected to a strong perpendicular magnetic field B, the cyclotron motion of electrons is quantized and their energy spectrum splits into a set of equally spaced discrete levels (Landau levels) designated by the orbital quantum number N (= 0, 1, 2, ...), with energy separation ħω_c, where ω_c = eB/m^* is the cyclotron frequency (m^*: effective mass). Each Landau level is further split into spin-up (↑) and spin-down (↓) levels separated by the Zeeman energy E_Z = |g|µ_BB, where µ_B = eħ/2m_e is the Bohr magneton (m_e: electron mass in vacuum) and g is the g-factor. The ratio of the Zeeman energy to the Landau level separation (m^*/m_e)•|g|/2, which is unity for electrons in vacuum, is significantly reduced in GaAs, by a factor of ~70 owing to the small effective mass m^* = 0.067m_e and the small g-factor (g = –0.44).

Fig. 5. Schematic illustrations of energy level splitting and electron configurations in a high magnetic field at different filling factors. Note that the energy splitting is not to scale.

Each spin-split Landau level has a degeneracy of n_φ = eB/h, so that Landau-level filling factor ν, defined as ν = nh/eB, represents the number of occupied levels. The electron configurations for Landau-level filling factor ν = 2, 5/2, and 5/3 are shown schematically in Fig. 5 with the simplistic model that each spin-split Landau level can accommodate only six electrons. The electrons enclosed by the dashed lines have equal numbers of up and down spins, so they do not contribute to the net spin polarization.

At ν = 2, the two lowest levels, (N = 0, ↑) and (N = 0, ↓), are fully occupied with equal numbers of spin-up and spin-down electrons, so the net spin polarization is zero. Thus, the peak position of the RD-NMR spectrum taken at ν = 2 marks the bare resonance frequency of the ⁷⁵As nuclei without a Knight shift.

At ν = 5/2, the N = 0 Landau levels are fully occupied with equal numbers of spin-up and spin-down electrons, so only those electrons in the N = 1 Landau level contribute to the spin polarization and hence to the Knight shift. The resonance spectrum for ν = 5/2 appears in the frequency range lower than the resonance frequency at ν = 2. The Knight shift measured from peak to peak is about 12 kHz. The finite Knight shift observed for ν = 5/2 clearly indicates that the electrons in the N = 1 Landau level forming the ν = 5/2 FQH state have non-zero spin polarization.

To convert the measured Knight shift into spin polarization, we need a control spectrum for a state with known (non-zero) polarization. For this purpose, we use the spectrum at ν = 5/3. As schematically shown in Fig. 5, 5/3 filling of electrons is equivalent to 1/3 filling of holes in the N = 0 Landau level. Since the ν = 1/3 state is fully polarized, the ν = 5/3 state is as well [60], which implies the electron configuration shown in Fig. 5. Note that we accessed different values of ν by changing the number of electrons while keeping B constant. Thus, the ratio of the number of electrons that contribute to spin polarization in the ν = 5/2 and 5/3 states is 3:2 if the ν = 5/2 state is fully polarized, and this is indeed what we observed. To determine the spin polarization more accurately, we fitted the measured spectra by taking into account the local electron density that varies along the direction normal to the 2D plane (solid lines in the figure). The simulation reproduces the observed spectral shape and confirms that the ν = 5/2 FQH state is fully polarized.