|
|||||||||||||
|
|
|||||||||||||
|
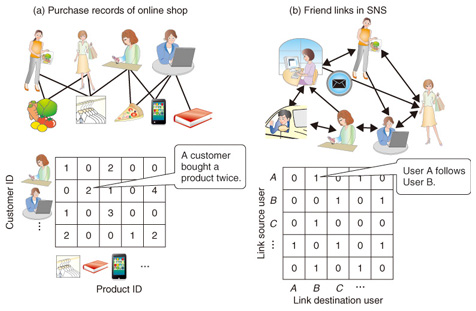
Feature Articles: Communication Science that Connects Information and Humans Vol. 10, No. 11, pp. 8–13, Nov. 2012. https://doi.org/10.53829/ntr201211fa2 Extracting Essential Structure from DataAbstractIn this article, we introduce part of our technique for analyzing and mining data matrices by using statistical machine learning approaches. The analysis of big data is becoming a hot trend in the information and communications technology (ICT) field, and automated computational methods are indispensable because the data volumes exceed manual capabilities. Statistical machine learning provides good solutions for this purpose, as we show in this article. 1. IntroductionThe analysis of big data is becoming a hot trend in the information and communications technology (ICT) business. However, there is no concrete definition of big data. Most of the data treated in big data analyses is characterized by its large amount, which greatly exceeds the amount that can be treated manually. For example, gigantic purchase records of an online commerce service are organized and managed by computers, and this data helps to generate product recommendations for each customer. And the servers used by Twitter, a well-known online social networking service (SNS) and microbloging service, handle more than 4.5 million tweets (messages) per day [1]. Analyzing trends in Twitter obviously requires computers to deal with this amount of digital data. We need an automated computational process and data mining technique to understand the characteristics of such big data and extract useful knowledge from it. However, they will not come into existence by themselves. We must choose a principle, or criterion, that defines the actual computation process and controls the data usage. NTT Communication Science Laboratories (CS Labs) is researching data mining techniques based on statistical machine learning that seek the best answers in the statistical and probabilistic senses. Statistical machine learning primarily handles numbers, i.e., numerical data. In this article, we assume that the data can be converted into a data matrix like the cells of a spreadsheet (Fig. 1). For example, we can convert the purchase records of an online shopping service by placing the customer’s identity (ID) on the vertical axis and the product ID on the horizontal axis. In the same manner, an SNS friend network can be converted into a data matrix. A friend relation, or a follower relation, between two users is defined by the source (user who follows) and the destination (user who is followed). Setting the source as the vertical axis and the destination as the horizontal axis, we obtain the data matrix of an SNS friend network. These are just examples: many kinds of data can be converted into data matrices.
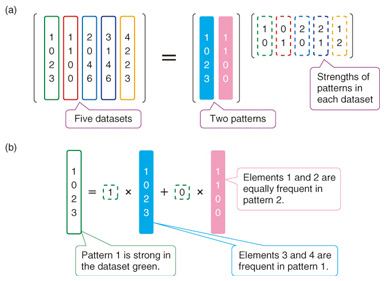
In this article, we introduce a few data mining techniques that are being studied and developed at NTT CS Labs. We use statistical machine learning techniques to model such data as structural relations between a small number of essential factors such as product purchase patterns or communities and hubs in networks. These methods automatically decompose complicated data and find essential factors without careful manual tuning thanks to statistical criteria. In sections 2 and 3, we introduce two remarkable methods: nonnegative matrix factorization (NMF) [3] and infinite relational models (IRMs). 2. Pattern extraction from real-valued data matrix by NMFNMF is applicable for a data matrix whose elements are nonnegative. Its goal is to decompose the data matrix into two smaller matrices: one representing patterns and the other representing the strengths of the patterns in each dataset. NMF finds two optimal nonnegative matrices in terms of the reconstruction errors with respect to the original data matrix (Fig. 2(a)). An example of how to interpret the NMF decomposition is shown in Fig. 2(b).
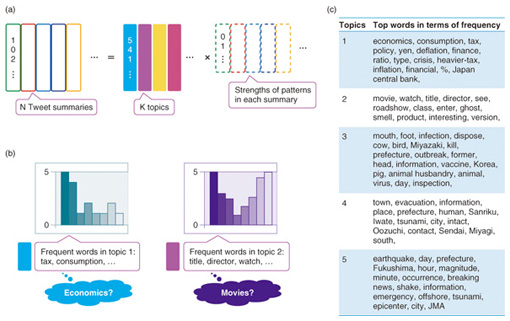
Let us consider the analysis of a newspaper data matrix. The data matrix consists of the word counts of the newspaper articles. Colored column vectors correspond to articles, and a number in a column vector represents the number of times a word appears in an article. In this case, the pattern matrix consists of column vectors, where each vector corresponds to a topic discussed in articles, such as sports, economics, and politics. Each pattern has its own word frequency distribution: thus, we can identify the contents of a pattern. Moreover, each article (dataset) has its own pattern strengths, as summarized in a strength matrix. Using this strength, we can easily summarize the contents of many articles. In summary, NMF extracts patterns and pattern strengths at the same time by decomposing the original data matrix. Here, we introduce an application of NMF to Twitter topic extraction. It is not an easy task to find and grasp topics existing in Twitter because of the number and variety of tweets. We tackle this problem by decomposing summary articles (summaries) in a content curation site, which presents collections of social media content voluntarily collected and reordered. In this task, the data matrix consists of a number of column vectors where each column vector corresponds to a summary. The elements in a column vector indicate the appearance frequencies of words in an summary (Fig. 3(a)). NMF gives patterns of word distributions corresponding to topics in Twitter (Fig. 3(b)) and the strengths of patterns within each summary at the same time.
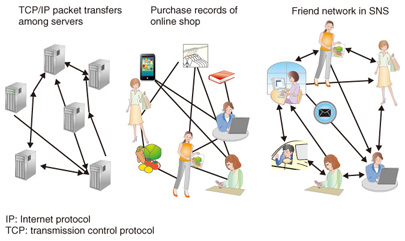
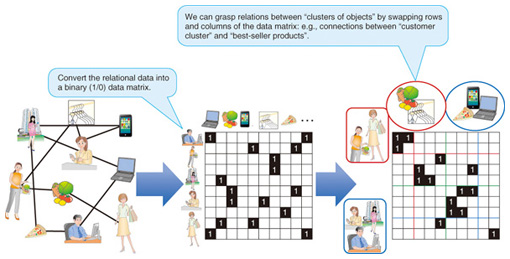
The results of analyzing approximately 100,000 summaries (summarizing approx. 10,000,000 tweets) from Feb. 2010 to Apr. 2011 are presented in Fig. 3(c). Extracted topics are very clear and easy to interpret. For example, the first topic is related to economics, the third topic corresponds to foot-and-mouth disease outbreaks in Miyazaki, the fourth topic concerns tsunamis at Sanriku in the previous Tohoku Earthquake, and the fifth topic is related to emergency earthquake warnings. 3. Relation cluster extraction from binary data matrix by IRMsIn this section, we introduce IRMs [4] that are especially applicable for relational data, which represents existences of relations between multiple objects. Examples of relational data are shown in Fig. 4. In general, relational data focuses on the structure of links between several objects (servers, customers, products, etc.).
We can convert such relational data into a binary data matrix, as in Fig. 5. The value 1 indicates the existence of a link, and the value 0 indicates the nonexistence of a link. Given the data matrix, IRM extracts some good groupings (colored partitions in the figure) by swapping and re-ordering row indices and column indices. By good, we mean that the resultant data matrix consists of partitions that are very white or black and not mixtures of white and black. In the case of Fig. 5, IRM extracts pairs of a “specific customer group” and “specific products frequently purchased by the members of the group”: in other words, relations between (customer) groups and (product) groups. If we apply IRM to SNS friend link data, we can find communities in the network links and interactions between communities.
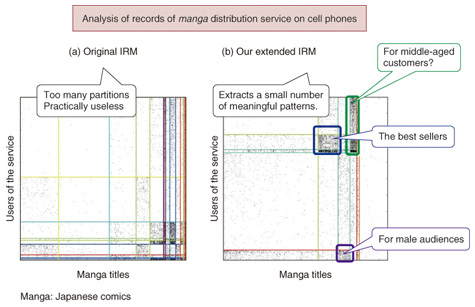
One benefit of using IRM is that it automatically decides the number of groups, or the cardinality of the partitions, in a statistically optimal manner. Thus, once a relational data matrix has been input, IRM takes care of the remaining tasks and enables analyses like the one described above. In this article, we would like to present two novel extensions of IRM developed by CS Labs. The first extension enables users to analyze time-varying relational data. Many relations change over time. For example, human connections in an organization gradually change day by day, and sometimes change drastically with a reorganization. Our IRM extension can represent such mixed changes in relations. In experiments, we analyzed email histories at Enron Corporation. Our method successfully extracted and tracked changes in a community of employees related to its financial and monetary sections, and a few key persons who were very influential throughout the company. Another of our recent achievements can handle problems induced by data sparsity, which is often observed in real-world purchase data. Most purchase history records in e-commerce are characterized by the very small number of actual purchases compared with the huge number of customer-product pair entries. When such data is converted into a data matrix, most of the matrix cells have the value 0; namely, the data matrix is sparse. The naïve IRM does not perform well on the sparse data matrix shown in the left panel of Fig. 6. It extracts so many groups that a lot of human effort is required to interpret and extract knowledge from the analysis results.
We extended IRM to extract only important purchase patterns from a sparse data matrix. Our key hypothesis is that products that everyone buys and that no one buys do not provide useful information for data mining. Similarly, users who buy nothing are also uninteresting. Our extended IRM automatically excludes objects that do not have specific patterns of relations, and the remaining interesting part of the data matrix is analyzed by IRM. An example of extended IRM is shown in the right panel of Fig. 6: the model successfully extracts a limited number of groups, and these groups are easy for the human eye to interpret. 4. ConclusionIn this article, we introduced two data mining techniques, NMF and IRM, for data matrices. The scope of statistical machine learning studies is limited to data matrices. CS Labs is committed to developing state-of-the-art machine learning technologies and is contributing to the development of data mining techniques for even larger and more complicated datasets. References
|
|||||||||||||