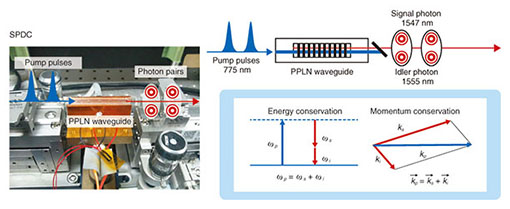
Distribution of Entangled Photon Pairs over 300 km of Optical Fiber

1. Introduction

A huge calculation time is required in order to solve certain mathematical problems such as factorization. The security of most modern cryptography schemes is ensured by achieving a high difficulty of solving such mathematical problems. The progress made in computers and algorithms, however, means that the calculation time may be drastically reduced in the future. Quantum cryptography, or quantum key distribution (QKD), has been proposed as a secure communication scheme based on a law of physics [1]. In a QKD system, a random key for a one-time pad cryptographic system is distributed from a sender (Alice) to a receiver (Bob) by sending single photons. According to Heisenberg’s uncertainty principle, a quantum state cannot be duplicated completely. This fundamental rule of physics protects the random key against eavesdroppers. When the eavesdroppers intercept the single photons and measure them to steal the information, the measurement inevitably disturbs the quantum states of the photons, which results in errors in the photon transmission between Alice and Bob. In this way, we can detect the eavesdropping by monitoring a change in the error rate and ensure the security of the random key.

QKD with a weak coherent light has already been implemented in field experiments at communication distances of tens of kilometers. A video-conference service based on QKD, for example, was demonstrated in the Tokyo QKD network in 2010 [2]. To increase the key distribution distance further, however, the loss in the communication channel is a primary issue that must be addressed. When we send a single photon over optical fiber, roughly 5% of the photons are lost in the optical fiber per 1-km transmission. This means that the success probability of the single-photon transmission over 300 km of optical fiber is less than 0.0001%. When the photon count rate becomes comparable to a dark count rate of a single-photon detector because of the transmission loss, we can no longer distinguish the transmitted signal. Hence, the communication range of the QKD is limited by the signal-to-noise ratio (SNR). Unfortunately, we cannot use an optical amplifier for the QKD because we also cannot duplicate the single photon without any errors.

Consequently, entanglement-based QKD has been proposed as a way to improve the SNR in long-distance QKD [3]. In this scheme, an entangled photon pair is distributed to each distant receiver from a halfway point of the communication channel. The success probability of the single-photon transmission increases because the transmission distance of each photon is reduced by half, and thus, we can improve the SNR compared with the conventional QKD. The quantum entanglement is a quantum state where each particle cannot be described as a quantum state independently. When we undertake a measurement on an entangled photon pair, the result for each photon is completely random, but the two results show a correlation, even when these two photons are separated by long distances. This correlation, which cannot be explained by classical theory, is an essential property of quantum entanglement.

NTT demonstrated entanglement-based QKD over 100 km of optical fiber in 2008 [4] and also performed long-distance entanglement distribution over 200 km in 2009 [5]. In this article, we introduce our recent experimental results for entanglement distribution over 300 km of optical fiber [6].

2. Generation and measurement of entangled photon pairs

For the long-distance entanglement distribution, we generate high-dimensional time-bin entangled photon pairs, which are suitable for fiber transmission [7]. We employ a spontaneous parametric down conversion (SPDC) process in a periodically poled lithium niobate (PPLN) waveguide to generate temporally correlated photon pairs, as shown in Fig. 1 [8]. The two generated photons, which are called signal and idler photons, conserve the total momentum and energy of the pump photon. In time-bin entangled state generation, we input coherent sequential pulses into the PPLN waveguide as a pump. If the pump power is small, and the probability that these pulses will generate photon pairs simultaneously is relatively small, we can generate a coherent superposition state of the photon pair states generated by those pump pulses. The whole state wave function of an entangled photon pair can be written approximately as:

where |k>_z denotes a state in which a single photon is found at the kth time slot in mode z (= s: signal, i: idler). Here, N is the number of pulses in which the phase coherence of the pump pulses is preserved. The generated signal and idler photons are separated by a wavelength filter and then launched into long-distance fibers.

Fig. 1. Spontaneous parametric down conversion in PPLN waveguide.

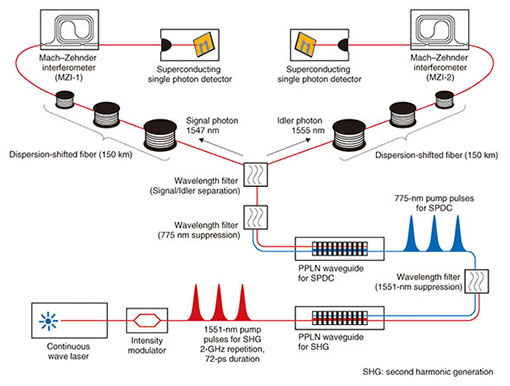
After the long-distance distribution of the entangled photon pair, we evaluate the distributed entanglement by measuring two-photon interference in a Franson-type experiment [9]. The distributed signal and idler photons are measured with n-bit delayed Mach–Zehnder interferometers (MZIs) followed by single-photon detectors. The n-bit delayed MZIs transform the |k>_zstate into the |k>_z+ exp(iθ_z)|k + n>_zstate (unnormalized), where θ_zis the relative phase between the two divided paths in each MZI. Under the condition of N >> n, the coincidence count rate between the signal and idler photons is approximately proportional to 1 + Vcos(θ_s + θ_i), where V is the visibility of the two-photon interference. In measuring the entanglement, although the photon count rate of the signal and idler photons is independent of the MZI phases, we will observe a change in the coincidence count between the signal and idler photons depending on the phases of the MZIs.

We also confirm the violation of Bell’s inequality to make sure that the two-photon interference is caused by the quantum mechanics. In the Bell’s inequality experiment, we measure a criterion value of S for the Clauser, Horne, Shimony, and Holt (CHSH) inequality [10]: |S| ≤ 2 for any correlations based on the classical mechanics. The S value is obtained by undertaking 16 coincidence count measurements, in which the 4 different phase values of MZIs are set for the signal and idler photon detection. The S value is given by

where d_z, d´_z (z = s, i) denote arbitrary values of phases θ_z in interferometers, and E(θ_s,θ_i) is defined as: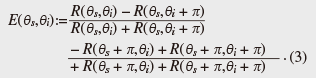

Here, R(θ_s, θ_i) is the coincidence count rate of a two-photon interference measurement when we set the phases of the MZIs for the signal and idler photons at θ_sand θ_i, respectively. Although the S value obtained in a measurement on any classically correlated photons does not exceed 2, the value for an entangled photon pair can be larger than 2 by selecting appropriate phase settings (violation of Bell’s inequality). Thus, we can distinguish between the correlations based on the quantum and classical mechanics depending on whether or not the obtained S value exceeds 2, respectively.

3. Experimental setup

Our experimental setup is shown in Fig. 2. The high-dimensional time-bin entangled photon pairs were generated by the SPDC process in the PPLN waveguide. We set the repetition rate of the sequential pump pulses as high as 2 GHz so that we can use the time domain efficiently. The generated signal and idler photons were separated by a wavelength filter and then launched into 150-km dispersion-shifted fibers. The distributed photons were launched into MZIs fabricated based on planar lightwave circuit technology. The propagation time difference between the two paths of the MZI was 1 ns, and thus, it worked as a 2-bit delay for 2-GHz repetition pulses. We were able to control the phases of θ_s and θ_iby tuning the temperature of MZI-1 and MZI-2, respectively. An output port of each MZI was connected to a superconducting single-photon detector (SSPD), which contributed to the low-noise and highly efficient detection of the entangled photon pairs. The SSPD had a low dark count probability of about 1 × 10⁻⁹ per 100-ps time window and a high detection efficiency of 20%. Output signals from the SSPDs were input into a time interval analyzer (TIA) as the start and stop signals for coincidence detection. The time resolution of the TIA was 9.8 ps, and the coincidence counts were collected in a 300-ps time window.

Fig. 2. Experimental setup for distribution of time-bin entangled photon pairs over 300 km of optical fiber.

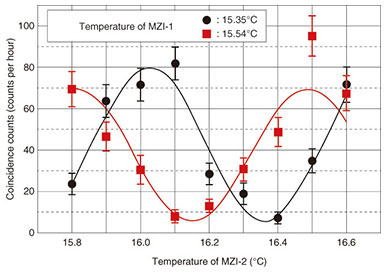
4. Two-photon interference and violation of Bell’s inequality

The experimental results of the two-photon interference by the distributed entangled photon pairs are shown in Fig. 3. First, we fixed θ_sby setting the temperature of MZI-1 at 15.35°C and swept the temperature of MZI-2 in 0.1°C steps while measuring the coincidence counts. The measurement time was 1 hour for each temperature setting. The corrected coincidence counts, which are raw data without the subtraction of accidental counts, are shown by the circles in Fig. 3, which show a clear sinusoidal modulation. The visibility of the fitted curve was 86.1 ± 6.8%. We then changed θ_swith the temperature of MZI-1 at 15.54°C and observed another fringe (squares), whose visibility was 83.7 ± 9.1%. Thus, we confirmed that a non-classical correlation was preserved even after the two photons were separated by as much as 300 km of fiber.

Fig. 3. Two-photon interference fringes obtained after 300-km distribution over fiber.

We then performed the S value measurement for the CHSH inequality. We searched for phase settings where the coincidence rate was maximized, and we defined these phases as θ_s0 and θ_i0. We used these phases to determine the measurement parameters in Eq. (2) as d_s = θ_s0, d´_s = θ_s0 + π / 2, d_i = θ_i0 + π / 4, and d´_i = θ_i0 − π / 4. We obtained 16 values of R(θ_s, θ_i) over 16 hours to obtain the S value. To improve the accuracy of the S value, we repeated the same experiments three times with the same measurement parameters. As a result, we found that S = 2.41 ± 0.14, leading to the violation of 2.9 standard deviations. This means that the correlation of the entangled photon pair clearly violates Bell’s inequality. We confirmed from this result that we achieved a high-quality entanglement distribution over 300 km of fiber.

5. Future work toward long-distance entanglement distribution

The distance of the entanglement distribution is limited by the SNR of the setup, in principle. It is possible to attempt a longer distance distribution as long as the noise in the system is sufficiently low. Even if we can ignore the noise, however, the success probability of the distribution decreases exponentially as the distance increases, and thus, the time required for the distribution also increases exponentially. To solve this problem, Briegel et al. proposed the concept of a quantum repeater [11] based on nested entanglement swapping [12], entanglement purification, and quantum memory. The quantum memory is a key device for the quantum repeater, as it can store the quantum state of the distributed photon and output it after an arbitrary time. NTT has been studying several kinds of quantum memories as part of efforts to realize a quantum repeater. These memories include an atomic ensemble in a solid-state material. In the future, we hope to realize long-distance quantum communication by combining our entanglement generation and distribution technologies with quantum memories.

References

Takahiro Inagaki Researcher, Quantum Optical State Control Research Group, NTT Basic Research Laboratories. He received the B.E., M.E., and Ph.D. in engineering science from Tohoku University, Miyagi, in 2007, 2009, and 2012, respectively. At Tohoku University, he was engaged in research on quantum state transfer between photon polarization and electron spin in a semiconductor. He joined the Quantum Optical State Control Research Group in NTT Basic Research Laboratories in 2012. He is currently engaged in research on quantum communication based on entanglement and electro-optic effects in a dielectric material. He is a member of the Physical Society of Japan (PSJ) and the Japan Society of Applied Physics (JSAP).

Hiroki Takesue Senior Research Scientist, Supervisor, Distinguished Researcher, Quantum Optical State Control Research Group, Optical Science Laboratory, NTT Basic Research Laboratories. He received the B.E., M.E., and Ph.D. in engineering science from Osaka University in 1994, 1996, and 2002, respectively. In 1996, he joined NTT Laboratories, where he was engaged in research on lightwave frequency synthesis, optical access networks using wavelength division multiplexing, and quantum optics. His current research interests include quantum optic experiments using nonlinear waveguides and quantum communication based on entanglement. He is the recipient of several awards, including the ITU-T Kaleidoscope Conference 2nd Best Paper Award in 2008 and The Commendation for Science and Technology by the Minister of Education, Culture, Sports, Science and Technology of Japan (The Young Scientists’ Prize) in 2010. From 2004 to 2005, he was a Visiting Scholar at Stanford University, Stanford, California. He is a member of IEEE (The Institute of Electrical and Electronics Engineers) and JSAP.