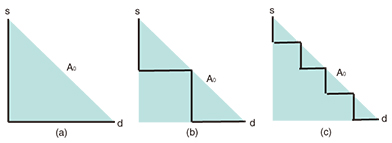
You need Adobe Reader 7.0 or later in order to read PDF files on this site.
If Adobe Reader is not installed on your computer, click the button below and go to the download site.

Regular Articles

Vol. 13, No. 6, pp. 23–28, June 2015. https://doi.org/10.53829/ntr201506ra1

Toward the Realization of Disaster-free Networks

Hiroshi Saito

Abstract

This article proposes a network concept called Disaster-free Network and the technologies used to implement it: a physical network design that is robust against spatial disaster, and network avoidance control. Two unique contributions are achieved with this research on the Disaster-free Network: a disaster management concept and a new area of research. The objective of a Disaster-free Network is to avoid or minimize encounters with disasters. This is a completely new concept of disaster management, which has previously been based on the provisioning and restoration of networks. The Disaster-free Network concept is implemented by appropriately designing or controlling the spatial and geographical shape of the network or the spatial and geographical locations of network objects. This kind of design and control is based on a method of evaluating the probability defined by geometrical events and opens up a new area of research.

Keywords: disaster management, spatial design and control, network vision

1. Introduction

Every year around the world, people suffer from disasters. Natural disasters are dominant as the direct causes of other disasters, and their number tends to be much larger than that of man-made disasters [1, 2]. In some countries, earthquakes are the largest threat among natural disasters. They are difficult to forecast, and their impact is huge. The earthquake that occurred in March 2011 in Japan triggered a massive tsunami, which served as a reminder of the severity of a huge earthquake [3]. Similar events that cause massive damage occur every few years worldwide [4]. In addition, global warming results in stronger and more devastating natural disasters, and the number of disasters increases exponentially [1]. Therefore, disaster management has become even more crucial for many network operators [5].

Historically, disaster management has been based on protection, which is sometimes called provisioning and restoration and sometimes called recovery [6]. Protection provides spare resources in advance, and restoration attempts to find resources that will accept traffic using the failed components. In addition, network operators use temporary systems when disasters occur. A transportable terrestrial station of a satellite communication system is such an example [7].

These historical approaches assume that we cannot avoid disasters, and they use the technologies for failure management. The Disaster-free Network concept takes a completely different approach [8] and attempts to avoid disasters as much as possible. The network design approach to implement the Disaster-free Network concept involves designing networks to, for example, minimize the probability of encountering disasters, and is mainly used for unforecastable disasters such as earthquakes. In addition, the disaster avoidance control in a Disaster-free Network reconfigures the mapping between the logical network and the physical network to minimize the probability of disconnection, for example, and is mainly used for forecastable disasters such as hurricanes. These technologies realize the Disaster-free Network concept and open a new avenue of research.

2. Physical network design

Making society, including the communication infrastructure, robust against earthquakes is a serious target in Japan because the possibility of a massive earthquake occurring is increasing. Although we have not had a method to design networks or a method to evaluate the effects of earthquakes, some studies have started investigating geographically correlated failures; several studies of network survivability have been reported that take account of spatial/geographical conditions [9–14]. Some other studies have investigated the location of the worst spatial/geographical disaster for a network [15–20].

Unfortunately, however, these studies do not directly intend to derive a geographical spatial design of a physical network. To respond to this situation, we have conducted a series of studies regarding the geographical spatial design of a physical network [21–23]. These studies assume that a given disaster area occurs with a uniform probability within an area A₀ of interest and can be categorized according to the assumption used for a disaster area—that is, whether a disaster area can be modeled by a half-plane or by a bounded region—and the assumption used for a link (node) failure—that is, whether part of a link (a node) always fails or fails with a certain probability if that part (the node) is in a disaster area. In the following section, the probability P(s,d) of a disconnection between s and d is used as a metric. P(s,d) is equivalent to the probability that none of the routes between s and d are connected. If a link always fails when part of a link is in a disaster area, P(s,d) is equal to the probability Q(s,d) of encountering the disaster. The notation Q(s,d) means that every route between s and d intersects a disaster area.

2.1 Probability Q(s,d) of encountering a disaster when the disaster area can be modeled by a half-plane [22]

The disaster area caused by an earthquake is sometimes huge—much larger than a regional network. In such cases, we can model the disaster area as a half-plane when we design the regional physical network. When the disaster area can be modeled by a half-plane, Q(s,d) can be expressed by explicit formulas for many network topologies and for many connectivity patterns such as the connectivity to either an active server or a standby server. For example, when there is a single physical route between s and d,

Q(s,d) = {L(A₀) + L(CH(r(s,d)))}/(2 L(A₀)),　(1)

where L(x) is the perimeter length of x, CH(x) is the convex hull of x, and r(s,d) is the route between s and d. According to Eq. (1), we can find that Q(s,d) for (a) is the largest, while that for (c) is the smallest in Fig. 1 because L(CH(r(s,d))) is largest for (a) and smallest for (c).

Fig. 1. Three tree networks.

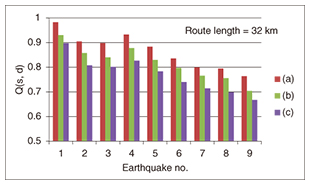
When s and d are on a convex ring physical network,

Q(s,d) = {L(A₀) + L(line(s,d))}/(2 L(A₀)),　(2)

where line(s,d) is the line segment between s and d. Equation (2) tells us that the geographical shape of the ring network is independent of Q(s,d) if it is convex. In addition, Eqs. (1) and (2) show that the effect of making a ring network is identical to making a straight line route regarding Q(s,d).

In addition to optimizing the geographical network configuration, it is also possible to optimize the standby server location and the number of standby servers using previously derived formulas [22]. For example, when s, d1, and d2 are on a ring network and s needs to be connected to d1 or d2, probability Q(s,d1 or d2) that there are no routes out of the disaster areas between s and d1 or between s and d2 is given by the following.

Q(s,d1 or d2) = {L(A₀) + L(line(s,d1)) + L(line(s,d1)) − L(CH(s,d1,d2))}/(2 L(A₀)),　(3)

where CH(s,d1,d2) is the convex hull of three points: s, d1, and d2. Because the difference between Eqs. (2) and (3) represents the effect of using the standby server, we can determine whether we should provide the standby server with Eqs. (2) and (3). In addition, Q(s, d1 or d2) is a function of the location of d1 and d2; we can determine their locations by minimizing Q(s, d1, d2).

2.2 Probability P(s,d) of disconnection between s and d, when the disaster area can be modeled by a half-plane, and a node or a link independently fails with a certain probability if a node or part of a link is in the disaster area [21]

Even when the disaster area can be modeled by a half-plane, P(s,d) cannot be expressed by an explicit formula, although an algorithm is given to calculate it for any network topology. When the network is a tree or a ring, the complexity of the algorithm is polynomial in the number of nodes. However, for a generic network topology, it is not polynomial. Although no explicit formulas are obtained, it is shown that reducing the perimeter length of the convex hull of a route reduces P(s,d). Therefore, the straight line route connecting each pair of consecutive nodes minimizes P(s,d) when the location of each node is fixed. In addition, the algorithm enables us to evaluate P(s,d) when the geographical configuration of part of the network changes. This is useful when it is necessary to partially remake the geographical configuration of the existing network.

Furthermore, the results obtained can be used to determine which parts of the network need to be updated with/without changing the geographical configuration. NTT laboratories have obtained statistics on the failure probabilities of old/new network components by investigating damage caused by past earthquakes, and therefore, P(s,d) can be evaluated using the results obtained when a certain part of the network is updated. As a result, we can determine which parts of the network need to be updated.

2.3 P(s,d) and Q(s,d) for bounded disaster area [23]

When the disaster area is not much larger than the network of interest, the shape of the disaster area has an impact on P(s,d) and Q(s,d). For the convex disaster area and a tree or convex ring network (or a combination of convex ring sub-networks), an optimal (or better) geographical configuration of the network regarding Q(s,d) and approximation formulas for P(s,d) are derived.

For a tree network, a short and zigzag route is better regarding Q(s,d). (See [23] for the formal definition of zigzag.) Our theoretical result asserts that Q(s,d) for (a) in Fig. 1 is again the largest, and that for (c) is the smallest. This result was confirmed by simulation using empirical data on nine earthquakes under the assumption that a disaster area caused by an earthquake randomly appears with a uniform intensity and intersects A₀. (These data regarding the disaster areas are based on maps released by the Japan Meteorological Agency (JMA) [24] and [25].) The simulation result shown in Fig. 2 verified the theoretical result, although the actual disaster area may not be convex.

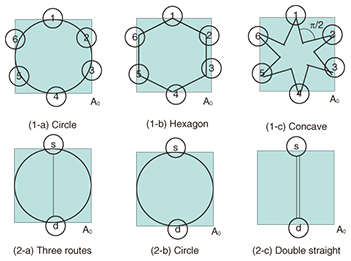
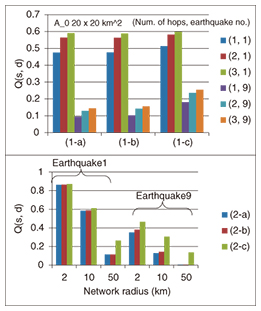
Fig. 2. Simulation result for single route between s and d [23].

For a ring network or a combination of convex ring subnetworks, additional routes within each ring network do not improve Q(s,d), and a smaller network than the original ring network increases Q(s,d). In Fig. 3, Q(s,d) for (1-a) is the smallest, while that for (1-b) is the second largest and that for (1-c) is the largest, where s,d = 1,…,6. In addition, Q(s,d) for (2-a) and (2-b) is the same, and that for (2-c) is the worst. The simulation result shown in Fig. 4 verified this theoretical result. (In Fig. 4, (2-a) is slightly better than (2-b) for earthquake 9. This is because the disaster area for this earthquake consists of several separated regions and does not satisfy the convexity assumption at all. For other earthquakes, the disaster area is not convex, but we cannot distinguish the result for (2-a) or for (2-b).)

Fig. 3. Two sets of three ring-network models.

Fig. 4. Simulation results for three ring-network models shown in Fig. 3 [23].

Approximation formulas for P(s,d) are derived under the assumption that the failure probabilities of nodes and links in a disaster area are very small. Let P₀(s,d) be P(s,d) under this assumption. Because Q(s,d) is P(s,d) when the failure probability is extremely high, P₀(s,d) and Q(s,d) give P(s,d) for the two extreme cases. However, optimality for Q(s,d) may not mean optimality for P₀(s,d). For example, P₀(s,d) for (2-a) may be better than P₀(s,d) for (2-b), although Q(s,d) values for (2-a) and (2-b) are the same. This is because the larger number of routes in a disaster area reduces P₀(s,d).

These results are also useful in determining a geographical configuration of the network that reduces P₀(s,d) or Q(s,d), the spatial/geographical server location that minimizes P₀(s,d), and also which part of the network should be updated. For a generic network, we need to divide the network into subnetworks with tree or ring topologies and apply the results to each subnetwork.

3. Network control

As a result of global warming, natural disasters such as hurricanes and tornados are increasing in intensity and frequency. However, advances in meteorology have enabled us to forecast them with a certain degree of accuracy. In addition, historical disaster data and hazard maps describing high-risk areas for each type of disaster have become public via the web. This means that we have time and data to react to the forecast results.

Disaster avoidance control [26] is a network control mechanism to reconfigure the network in order to prevent damage from a forecasted disaster, specifically, by reacting to the forecast results as they are updated. Of course, it is difficult to move network buildings, poles, and ducts. However, we can relocate software objects and data, and we can reconfigure logical networks or how they are mapped to the physical network. In particular, the progress in software technologies has expanded what we can do in disaster control efforts, and many network functions have become portable and relocatable. Software-defined networking and network functions virtualization are examples of technologies that enable these actions.

The disaster avoidance control algorithm to relocate software objects from a high-risk region to a low-risk region is described as follows as an example. When we receive a warning of a weather disaster for a certain region issued by a meteorological bureau, if this warning specifies a very small region, we identify the network components in the target (warning) region and their failure probabilities under the forecasted disaster and calculate a metric such as a probability of disconnection. However, it is often the case that the warning region is an entire city or prefecture, and the actual disaster area is a certain small area within the warning region. For such cases, we can apply a similar technique to one used in network design. That is, we assume that a given disaster area occurs with a uniform expected occurrence probability within the warning region and calculate a metric.

If the calculated metric exceeds a threshold, the disaster avoidance control will move some objects from the warning region to another region. The region or nodes that accept the objects can be chosen according to a similar or the same metric calculated with the constraint of the resources required by objects that should be relocated. When the new location is determined, we execute the relocation of objects from nodes in the warning region to nodes in the other region to avoid the disaster. Even if the relocation is executed, the services using these objects are not expected to be disrupted.

We developed an experimental system in which voice over Internet protocol (VoIP) call state data of each session can be relocated from one working Session Initiation Protocol (SIP) server in a high-risk region to another SIP server in a low-risk region. In this system, we confirmed that VoIP call state data of a session were effectively relocated without suspending the service.

4. Conclusion

This article proposed the concept and implementation of a Disaster-free Network. This concept attempts to reduce or minimize the possibility of a network encountering disasters. This is a completely different approach from that of conventional disaster management, and it creates a new direction for disaster management research.

The Disaster-free Network concept is based on the analysis of spatial relationships between a disaster area and a network. Therefore, if we apply this same approach to a topic other than disasters and analyze the relevant spatial relationships, we may be able to create other new network concepts.

References

[1]	E. Asimakopoulou, N. Bessis, S. Sotiriadis, F. Xhafa, and L. Barolli, “A Collective Intelligence Resource Management Dynamic Approach for Disaster Management: A Density Survey of Disasters Occurrence,” Proc. of IEEE INCoS 2011 (Third IEEE International Conference on Intelligent Networking and Collaborative Systems), pp. 735–740, Fukuoka, Japan, Nov./Dec. 2011.
[2]	C. Doerr and F. A. Kuipers, “All Quiet on the Internet Front?”, IEEE Communications Magazine, Vol. 52, No. 10, pp. 46–51, Oct. 2014.
[3]	M. Kobayashi, “Experience of Infrastructure Damage Caused by the Great East Japan Earthquake and Countermeasures against Future Disasters,” IEEE Communications Magazine, Vol. 52, No. 3, pp. 23–29, Mar. 2014.
[4]	Y. Ran, “Considerations and Suggestions on Improvement of Communication Network Disaster Countermeasures after the Wenchuan Earthquake,” IEEE Communications Magazine, Vol. 49, No. 1, pp. 44–47, Jan. 2011.
[5]	B. Mukherjee, M. F. Habib, and F. Dikbiyik, “Network Adaptability from Disaster Disruptions and Cascading Failures,” IEEE Communications Magazine, Vol. 52, No. 5, pp. 230–238, May 2014.
[6]	M. F. Habib, M. Tornatore, F. Dikbiyik, and B. Mukherjee, “Disaster Survivability in Optical Communication Networks,” Computer Communications, Vol. 36, No. 6, pp. 630–644, Mar. 2013.
[7]	The 2nd Workshop on Digital Broadcasting, Japan Society for Disaster Information Studies, “Activity Report on ‘Collaboration between Broadcasting and Telecommunication’ Workshop,” Oct. 2007 (in Japanese). http://www.jasdis.gr.jp/06chousa/2nd/s4_siryo.pdf
[8]	H. Saito, “Concept and Implementation of Disaster-free Network,” Keynote of DRCN 2015 (11th International Conference on Design of Reliable Communication Networks), Kansas City, USA, Mar. 2015.
[9]	S. Neumayer and E. Modiano, “Network Reliability with Geographically Correlated Failures,” Proc. of INFOCOM 2010 (29th IEEE International Conference on Computer Communications), San Diego, USA, Mar. 2010.
[10]	W. Wu, B. Moran, J. H. Manton, and M. Zukerman, “Topology Design of Undersea Cables Considering Survivability under Major Disasters,” Proc. of WAINA 2009 (23rd IEEE International Conference on Advanced Information Networking and Applications Workshops), pp. 1154–1159, Bradford, UK, May 2009.
[11]	C. Cao, M. Zukerman, W. Wu, J. H. Manton, and B. Moran, “Survivable Topology Design of Submarine Networks,” J. Lightwave Technol., Vol. 31, No. 5, pp. 715–730, Mar. 2013.
[12]	A. Sen, B. H. Shen, L. Zhou, and B. Hao, “Fault-Tolerance in Sensor Networks: A New Evaluation Metric,” Proc. of INFOCOM 2006 (25th IEEE International Conference on Computer Communications), Barcelona, Spain, Apr. 2006.
[13]	M. T. Gardner and C. Beard, “Evaluating Geographic Vulnerabilities in Networks,” Proc. of CQR 2011 (2011 IEEE International Workshop Technical Committee on Communications Quality and Reliability), pp. 1–6, Naples, Italy, May 2011.
[14]	M. T. Gardner, R. May, C. Beard, and D. Medhi, “Using Multi-topology Routing to Improve Routing during Geographically Correlated Failures,” Proc. of DRCN 2014 (10th International Conference on Design of Reliable Communication Networks), pp. 1–8, Ghent, Belgium, Mar./Apr. 2014.
[15]	D. Bienstock, “Some Generalized Max-flow Min-cut Problems in the Plane,” Math. Oper. Res., Vol. 16, No. 2, pp. 310–333, May 1991.
[16]	S. Neumayer, A. Efrat, and E. Modiano, “Geographic Max-flow and Min-cut Under a Circular Disk Failure Model,” Proc. of INFOCOM 2012 (31st IEEE International Conference on Computer Communications), Toronto, Canada, Mar. 2012.
[17]	S. Neumayer, G. Zussman, R. Cohen, and E. Modiano, “Assessing the Vulnerability of the Fiber Infrastructure to Disasters,” IEEE/ACM Trans. Networking, Vol. 19, No. 6, pp. 1610–1623, Dec. 2011.
[18]	P. K. Agarwal, A. Efrat, S. Ganjugunte, D. Hay, S. Sankararaman, and G. Zussman, “The Resilience of WDM Networks to Probabilistic Geographical Failures,” Proc. of INFOCOM 2011 (30th IEEE International Conference on Computer Communications), pp. 1521–1529, Shanghai, China, Apr. 2011.
[19]	Y. Zhang, J. Y. Wang, and W. Li, “Assessing the Safety Risk Grade of Optical Network from the Network Geography Distribution,” Proc. of ICCT 2012 (14th IEEE International Conference on Communication Technology), pp. 709–712, Chengdu, China, Oct. 2012.
[20]	S. Trajanovski, F. A. Kuipers, A. Ilic, J. Crowcroft, and P. V. Mieghem, “Finding Critical Regions and Region-disjoint Paths in a Network,” IEEE/ACM Trans. Networking, submitted for publication.
[21]	H. Saito, “Geometric Evaluation of Survivability of Disaster-affected Network with Probabilistic Failure,” Proc. of INFOCOM 2014 (33rd IEEE International Conference on Computer Communications), pp. 1608–1616, Toronto, Canada, Apr./May 2014.
[22]	H. Saito, “Analysis of Geometric Disaster Evaluation Model for Physical Networks,” IEEE/ACM Trans. Networking, to appear. DOI: 10.1109/TNET.2014.2339356.
[23]	H. Saito, “Spatial Design of Physical Network Robust against Earthquakes,” J. Lightwave Technol., Vol. 33, No. 2, pp. 443–458, Dec. 2014.
[24]	Japan Meteorological Agency, Tokyo, Japan, “Estimated Seismic Intensity Distribution Map” (in Japanese). http://www.data.jma.go.jp/svd/eew/data/suikei/
[25]	Disaster Management, Cabinet Office, Tokyo, Japan, “Overview of the Great Hanshin-Awaji Earthquake” (in Japanese). http://www.bousai.go.jp/kyoiku/kyokun/hanshin_awaji/earthquake/index.html
[26]	H. Saito, R. Kawahara, and T. Fukumoto, “Proposal of Disaster Avoidance Control,” Proc. of Networks 2014 (16th International Telecommunications Network Strategy and Planning Symposium), Funchal, Madeira Island, Portugal, Sept. 2014.

Hiroshi Saito: Executive Research Engineer, NTT Network Technology Laboratories.
He graduated from the University of Tokyo with a B.E. in mathematical engineering in 1981, an M.E. in control engineering in 1983, and a Dr.Eng. in teletraffic engineering in 1992. He joined NTT in 1983. His research interests include traffic technologies of communications systems, network architecture, and ubiquitous systems. He has served as an editor and guest editor of technical journals including Performance Evaluation, IEEE Journal of Selected Areas in Communications, and IEICE Trans. on Communications, and as the organizing or program committee chairman of several international conferences. He was the Director of Journal and Transactions of IEICE and is currently an editorial board member of Computer Networks. Dr. Saito is a fellow of IEEE (Institute of Electrical and Electronics Engineers), IEICE (Institute of Electronics, Information and Communication Engineers), and ORSJ (Operations Research Society of Japan), and a member of IFIP (International Federation for Information Processing) Working Group 7.3. More information can be found at http://www9.plala.or.jp/hslab.

↑ TOP