Lossless Wavelength Conversion of Single Photons

1. Introduction

Wavelength (frequency, color) is an important physical parameter of light, and wavelength conversion is essential in current photonics technologies. Applications of wavelength conversion range from simple devices such as laser pointers to the fields of communications, precision measurement, and biomedical sciences.

Wavelength conversion of single photons is crucial for quantum communication, which holds promise for applications such as quantum cryptography and quantum teleportation. For example, the telecommunications wavelength is the wavelength that is suitable for long-distance transmission of photons in optical fiber networks. However, many physical systems such as atoms are sensitive to light with wavelengths in the visible band. In addition, even within the same wavelength band, the wavelengths and spectral shape of photons generally differ from each other depending on the physical properties of the photon sources or on the wavelength channel used for the transmission. Hence, the ability to harness the wavelength of photons, ideally in a lossless manner for scalability, is required in order to distribute quantum information between distant sites via interactions between light and matter or between different light sources.

2. Methods of single-photon wavelength conversion

The wavelength conversion of intense optical pulses induced by themselves (i.e., self-induced) in an optical fiber is shown in Fig. 1. The optical pulses, whose initial center wavelength was 1 µm in this example, acquired new wavelength components via nonlinear optical effects (self-phase modulation, four-wave mixing, stimulated Raman scattering, etc.), which can be easily induced by intense optical fields. However, the intensity of a single-photon wave packet is more than 10 orders of magnitude lower than that of ordinary laser pulses.

Fig. 1. Self-induced wavelength conversion of intense optical pulses with a center wavelength of 1 μm in an optical fiber. The input power was increased from (a) to (c). The output field was diffracted onto the screen by an external grating (not shown).

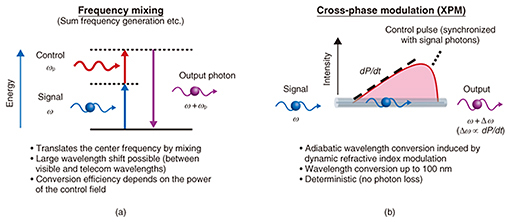
The first experimental demonstration of wavelength conversion was conducted in 1992. Since then, wavelength conversion of nonclassical light has been widely investigated using nonlinear three- or four-wave mixing (Fig. 2(a)), where photon wavelengths can be converted with mediation provided by the energy of other input pump fields [1]. While the intense pump required for a highly efficient conversion tends to simultaneously create noise photons, the demand for scalable quantum networking provides strong motivation for researching the simultaneous realization of lossless and noiseless conversion.

Another nonlinear optical interaction that enables frequency conversion is cross-phase modulation (XPM) (Fig. 2(b)), which is a third-order nonlinear optical effect that enables the phase of an optical (signal) field to be controlled by another (control) field. XPM provides a function for the wavelength conversion via dynamic phase alteration of an optical field in the following way. The presence of a control pulse with an intensity profile P(t) leads to an intensity-dependent variation in the refractive index variation of the material, which is experienced by the signal field as a phase shift φ(t) = 2γP(t)L, where γ is the nonlinearity strength of a medium and L is the device length. This gives rise to the instantaneous frequency shift

of the signal photons. Hence, we can add a wavelength shift, which is proportional to the time derivative of the control field intensity, to the single photons.

Fig. 2. Nonlinear optical effects for single-photon wavelength conversion.

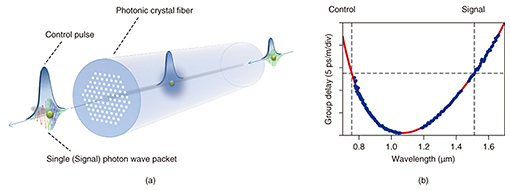
Unlike frequency-mixing based schemes, wavelength conversion can be accomplished without any photon loss because the XPM process deterministically occurs regardless of the control field intensity. For example, if we consider standard nonlinear optical fiber (γ = 0.01 /W/mm, L = 10 m) and standard picosecond optical pulses (dP/dt = 600 W/1 ps), we can obtain Δv(t) = 19 THz, which corresponds to a wavelength shift over 150 nm.

The quantum field to be converted now has a considerably lower intensity than that of the control pulses. Accordingly, a large frequency separation is needed between the two interacting fields in order to eliminate potential noise caused by the nonlinear spectral broadening of the control pulse. Moreover, the two interacting fields must propagate at the same pace; otherwise, φ(t) will become constant over the entire wave packet and cancel the frequency shift.

To fulfil the criterion, we used a photonic crystal fiber (PCF) as a Kerr medium with the dispersion property shown in Fig. 3. It exhibits two widely separated wavelengths with the same group velocity, thanks to the dispersion property, which is managed by arranging the air-hole claddings that surround the silica core.

Fig. 3. (a) Schematic of the experimental method. (b) The measured group-delay spectrum of the photonic crystal fiber.

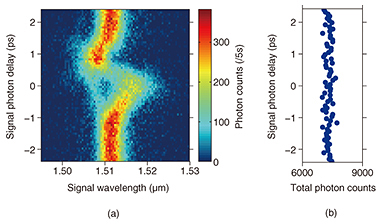
3. Experimental results [2]

We converted the wavelength of heralded single photons created via type-II spontaneous parametric down-conversion (SPDC) in a periodically poled potassium titanyl phosphate crystal. The center wavelength of the control field λ_c was chosen to be 756 nm, which satisfies v_g(λ_c) ~ v_g (2λ_c), where v_g is the group velocity of the PCF (Fig. 3(b)). In this way, both the XPM control pulses and SPDC excitation pulses can be fed from a pulsed laser source. The peak power of the control pulses coupled to the PCF was approximately 350 W.

The dependence on signal delay of the signal photon spectra heralded by the detection of idler photons is shown in Fig. 4(a). The heralded spectrum was markedly modified as the delay time varied. For instance, at the negative delay, where the signal photons are mainly synchronous at the falling edge of the control pulses in the PCF, the spectrum was entirely red shifted because dP/dt > 0. In contrast, the spectrum was blue shifted at the positive delay.

Numerical simulation of the frequency modulation was performed based on coupled nonlinear Schrödinger equations including XPM, self-phase modulation, and dispersion. The simulation result (not shown) well described the characteristics of the spectral shifts seen in the experimental data. The maximum wavelength shift was 3.2 nm (0.4 THz), which was limited by the length and the group velocity dispersion (GVD) of the PCF used. Further dispersion engineering of PCFs will be useful for reducing the GVD, which will lead to a larger wavelength shift.

The sum of the photon counts for each delay time is plotted in Fig. 4(b). The total coincidence count remains constant regardless of the delay, demonstrating that the conversion occurred without an observable photon loss. Hence, we have successfully achieved lossless wavelength conversion of single photons.

Fig. 4. Experimental results. (a) Delay dependence of the marginal distribution of heralded single (signal) photons. (b) Total photon counts as a function of the delay time.

We applied the scheme to further control the quantum correlation of pairs of photons. The demonstrations included modulation of nonclassical frequency correlation, interference, and entanglement between distant photons [2]. These results demonstrate our scheme’s applicability to a wide range of quantum information science and technologies, including computation and metrology.

4. Outlook

We are attempting to further improve the bandwidth and controllability of wavelength conversion. This can be achieved by further engineering the dispersion property of the photonic crystal fiber or engineering the temporal shape of the control pulses. The scheme, achievable in an optical fiber, is compatible with the equipment in optical communications networks. With this feature, we aim to develop a photon wavelength interface for flexible quantum networking.

References

Nobuyuki Matsuda Distinguished Researcher, Quantum Optical State Control Research Group, NTT Basic Research Laboratories. He received a B.E., M.E. and Ph.D. in electrical engineering from Tohoku University, Miyagi, in 2005, 2006, and 2009. In 2009 and 2014 he was a visiting research scholar at University of Bristol, UK. He joined NTT Basic Research Laboratories in 2010 and has since been engaged in research on integrated quantum photonics and single-photon nonlinear optics. He is a member of the Optical Society (OSA), the Physical Society of Japan, and the Japan Society of Applied Physics.