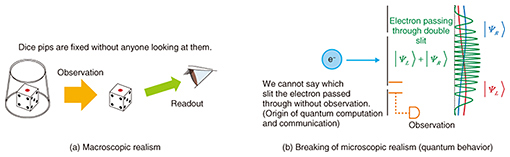
Demonstration of Realism Violation on a Macroscopic Scale

1. Introduction

What is realism? Suppose we have a single die (one of a pair of dice) underneath a cup. If we lift the cup and look at the die, we can see which pips (dots) are on the top surface (1, 2, 6, etc.). We assume that the pips on the die were predetermined before we lifted the cup (Fig. 1(a)). The idea of considering objects to be predetermined regardless of our observation of them is called realism. In our daily life, we cannot observe any phenomenon that contradicts this realism concept, which seems to support the validity of realism in the macroscopic world.

However, it is known that microscopic particles obey quantum mechanics, and as such, these particles can sometimes display counterintuitive phenomena. As an example, we can conduct an experiment where a single electron passes through a double-slit. If we take just a few measurements of the position of the single electron after passing through the double-slit, the measurements seem to be random. However, if we take many measurements in order to obtain statistical results, the electron position shows an interference fringe, which is typically observed as a wave that passes through both slits. It is worth mentioning that although we cannot divide the single electron into two, this result shows the possibility that the electron spin actually passed through both slits. We can understand this counterintuitive result as a realization of quantum superposition that is described by quantum mechanics. The electron shows a superposition between the state of passing through the right slit and the left slit.

Interestingly, if we observe the path of the electron by placing a detector at one of the slits, the interference fringe disappears. This can be easily understood as the situation in which we can determine the path of the electron by our observation of it, which also indicates that an object state (such as the path of an electron) is not determined until some observations are performed. This kind of phenomenon has been observed in many microscopic systems that obey quantum mechanics (Fig. 1(b)).

Fig. 1. (a) Realism in macroscopic world and (b) realism breaking in microscopic world.

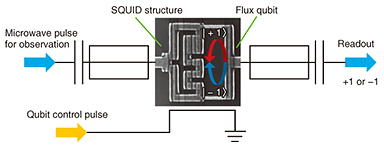
Because macroscopic objects are composed of microscopic systems such as atoms and electrons, we may think that macroscopic objects should also obey quantum mechanics (why would they not do this?). However, as the example of the die illustrates, realism seems to be valid in the macroscopic world from our experience. Whether the application of quantum mechanics has a limitation based on size or not has been an unsolved problem ever since the discovery of quantum mechanics. NTT has now demonstrated the violation of realism caused by quantum mechanics in the macroscopic world.

2. Testing the violation of realism

In the macroscopic world, it is thought that the state of objects is not disturbed if we implement optimal observations. For example, we can easily observe the pips on a die without disturbing the die. If we observe objects at different times, we can calculate temporal correlations between the observation results. It is known that if the observation does not induce a disturbance and realism is true, then the temporal correlation obtained by the experimental results should satisfy a specific condition called the Leggett-Garg inequality. This means that if the temporal correlation obtained by experimental observation without disturbance shows a violation of the Leggett-Garg inequality, this result indicates that realism is no longer valid. At NTT Basic Research Laboratories, we found an experimentally more feasible condition that is mathematically equivalent to the Leggett-Garg inequality, so we conducted tests to determine whether our condition was violated as a macroscopic realism challenge.

3. Superconducting flux qubit

We tested macroscopic realism using a superconducting flux qubit, which has been used in many investigations of quantum mechanics. The flux qubit is composed of a number of Josephson junctions. A Josephson junction can be regarded as an inductance similar to an induction coil. This inductance is dependent on the current, so Josephson junctions are a nonlinear inductance. If we fabricate a loop structure with these Josephson junctions, the circuit can form an effective two-level system (qubit) by applying optimal bias magnetic fields. The state of this artificial qubit is then composed of clockwise and anticlockwise currents. Interestingly, the current of this state is around 100 nA, which corresponds to a current of 10¹² electrons per second. This is an ideal device for checking whether or not quantum superposition can exist at the macroscopic level.

4. Quantum state observation

It is worth mentioning that even if the realism is true, a disturbance induced by the observation could provide us with a violation of the Leggett-Garg inequality. For example, if a die is underneath a cup and we lift up the cup, the cup itself may touch the die. Consequently, the position of the die (and thus, the pips that are apparent) could be changed by this observation, which also demonstrates a violation of the Leggett-Garg inequality. Therefore, to test macroscopic realism, it is crucial to carry out observations with as little disturbance as possible.

We used a superconducting quantum interference device (SQUID) embedded in a microwave resonator to observe the flux qubit with minimal disturbance. The states of the superconducting flux qubits can be distinguished by the magnetic fields from the device because the currents in the two states flow in opposite directions. The SQUID is magnetically coupled with the flux qubit, and the state of the flux qubit changes the inductance of the SQUID. The change in the inductance can be detected by the transmitted microwave of the resonator. Since this readout does not change the Josephson junctions into voltage states, we can implement a quantum non-demolition measurement^*1 that is known to have a small disturbance on the system (Fig. 2).

Fig. 2. Readout and control of superconducting flux qubit.

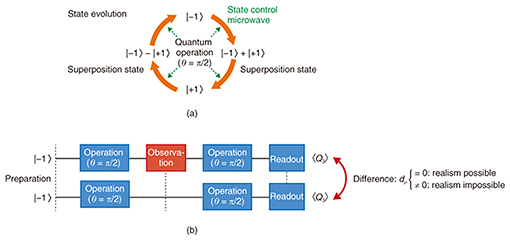
5. Experimental method

If the superconducting flux qubit obeys quantum mechanics, we should be able to generate a superposition state with a specific gate operation, which we call a quantum state operation. Microwave pulses are used to perform the quantum state operations in our experiments. We set the microwave frequency to be the same as the resonance frequency of the flux qubit, enabling us to control the flux qubit state by changing the amplitude or length of the pulse. We define |−1⟩ and |+1⟩^*2 as the states for the flux qubit. A long period of thermal relaxation initializes the flux qubit state into the |−1⟩ state. When our quantum state operations are performed, our state will evolve as

as shown in Fig. 3(a). When the quantum state operations are applied four times, the state returns to the initial state, which is similar to a rotation with a 2π angle. We call this operation a π/2 pulse. Next, |−1⟩ + |+1⟩ represents a specific quantum superposition state. The objective of our experiment is to check if such a superposition actually exists where the state is not determined until carrying out our observation.

If our qubit obeys quantum mechanics, we should be able to realize the superposition state of |−1⟩ + |+1⟩ by applying the π/2 quantum pulse to the |−1⟩ state. Without any observation, we can keep the superposition state; thus, an additional quantum operation induces a state of |+1⟩. The measurement result on this |+1⟩ state is always +1. In contrast, if we observe the |−1⟩ + |+1⟩ state, the observation stochastically projects our state into a |−1⟩ or |+1⟩ state. In this case, an additional quantum operation after the observation provides us with the states of |−1⟩ + |+1⟩ or |−1⟩ − |+1⟩, where the expectation value of the measurement result is 0.

We can also consider a case when the realism is correct and perform two experiments (Fig. 3(b)). One of them contains two π/2 operations; we observe the system between these operations. The other experiment is composed of two π/2 operations without an observation between them. Since we can observe without any disturbance (or only a negligible disturbance), any observation between the operations should not change the state of the objective. Therefore, the measurement results for these two experiments should be the same.

Fig. 3. (a) Quantum state operation and (b) sequence of experiment.

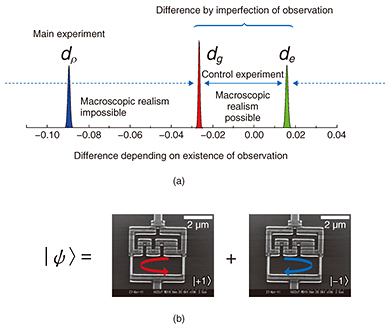
For the reasons explained above, we should observe a difference between these two experiments if our superconducting flux qubit obeys quantum mechanics, while there should be no difference if the realism is correct. We refer to this as our main experiment. However, since any observation must have a finite disturbance, we need to quantify the disturbance in the other experiment, which we call the control experiment. This can be done as follows. We prepare the state |−1⟩ or |+1⟩, observe the state, and read it out. Then we repeat the same experiment without the observation in the middle. By comparing the difference in the readout results, we can estimate the degree of disturbance that occurs with our observation.

We can now examine how the observation between the quantum operations affects our readout results. For an initial state of |−1⟩ (|+1⟩), we define the difference in the readout between two experiments as d_g (d_e) in the control experiment and d_ρ for our main experiment. If realism is true, d_ρ should be between d_g and d_e, because the state is predetermined before the observation. On the other hand, if d_ρ is outside the region between d_g and d_e, we can conclude that the realism is not valid in this system.

6. Experiment

In our experiment, the energy difference between the two states of the superconducting flux qubit is several gigahertz. To avoid an unwanted thermal effect, we need to reduce our fridge temperature until the thermal energy was much lower than the qubit energy. For this purpose, we used a specific apparatus called a dilution refrigerator that realizes a temperature around 10 mK in our experiment.

By performing our experiment using a superconducting flux qubit, we obtained the values of d_ρ, d_g, and d_e as displayed in Fig. 4(a). Interestingly, d_ρ appears beyond the region between d_g and d_e. This clearly shows that the dynamics of the superconducting flux qubit cannot be explained by the realism despite the macroscopicity of the flux qubit (Fig. 4(b)). Furthermore, our experimental results demonstrated the breaking of realism in the superconducting flux qubit current states by 84 times the standard deviation [1].

Fig. 4. (a) Experimental result and (b) quantum superposition of current state.

7. Future plans

We demonstrated that quantum mechanics can be applied on a macroscopic scale with a large supercurrent, where the device itself can be observed with an optical microscope. Our results are crucial in understanding the basics of quantum mechanics. In the future, we aim to conduct measurements with much less observation disturbance and to increase the macroscopic nature of the system by using a larger supercurrent qubit or an ensemble of superconducting flux qubits in order to understand quantum mechanics on a more macroscopic scale.

Reference

[1]	G. C. Knee, K. Kakuyanagi, M-C. Yeh, Y. Matsuzaki, H. Toida, H. Yamaguchi, S. Saito, A. J. Leggett, and W. J. Munro, “A Strict Experimental Test of Macroscopic Realism in a Superconducting Flux Qubit,” Nat. Commun., Vol. 7, 13253, 2016.