|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
Feature Articles: A New Era in Quantum Information Processing Technologies Vol. 15, No. 7, pp. 22–27, July 2017. https://doi.org/10.53829/ntr201707fa5 Coherent Coupling between 4300 Superconducting Flux Qubits and a Microwave ResonatorAbstractA superconducting flux qubit can be used as a magnetic field sensor, and this has potential applications in many fields such as medical science and biology. If we could realize an entanglement between the superconducting flux qubits, it is expected that such a device would show much better sensitivity than any existing magnetic field sensors. We introduce here our recent research along this direction. Keywords: superconducting qubit, quantum computation, quantum sensing 1. IntroductionSensitive magnetic field sensing has many potential applications in medical science and biology. Magnetic resonance imaging (MRI) is a standard technique to obtain three-dimensional (3D) images of materials by detecting their magnetic field information. Magnetoencephalography provides a way to measure the electrical activity of the brain, and this has an important role in medical science. If we can improve the sensitivity of magnetic field sensors, we could characterize materials from high-resolution 3D imaging, or we could target the location of tumors before surgery by detecting small signals. There are many potential candidates to achieve a sensitive magnetic field sensor. One promising example is the quantum bit (qubit*1), which has been the subject of much theoretical and experimental research. The technology for fabricating qubits has mainly been developed for the purpose of implementing quantum computation. However, some types of qubits can be strongly coupled with external fields such as magnetic fields and electrical fields, so it is also possible to use qubits for sensing technology.
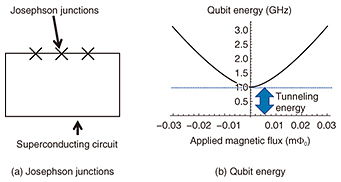
2. Superconducting flux qubitAmong the many possible candidates for qubit-based field sensing, we have investigated a superconducting flux qubit for quantum metrology. A superconducting qubit is an artificial atom, so we can easily design and characterize the device with the desired parameters (a significant advantage to achieve scalability [1]). The flux qubit is composed of a loop structure containing three Josephson junctions*2 (Fig. 1(a)). With the application of magnetic flux (n+0.5)φ0, where φ0 denotes the quantized magnetic flux and n an integer number, this device acts as a qubit. The resonant frequency of this qubit can be tuned by applying magnetic flux, so a change in magnetic fields can be detected by measuring the resonant frequency. A superconducting flux qubit has two states corresponding to clockwise and anticlockwise persistent current states. When we apply φ0 magnetic flux, the transition energy from the ground state to the excited states reaches a minimum (Fig. 1(b)). The difference between the ground and excited state is called the tunneling energy.
It is also possible to improve the sensitivity if we increase the number of superconducting flux qubits. In particular, if we create an entanglement*3 that does not exist in the classical world, we can achieve a sensor that has in principle much better performance than any existing devices. For example, superconducting quantum interference devices (SQUIDs)*4 are used in the medical sciences, but the sensitivity of an entanglement sensor composed of millions of superconducting flux qubits would be a few orders of magnitude higher than that of a SQUID [2].
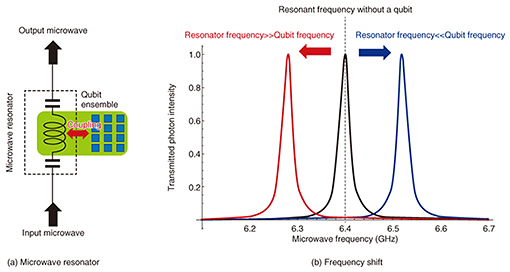
3. Coupling of microwave resonator and superconducting flux qubitsA microwave resonator is a natural way to achieve large-scale entanglement between multiple superconducting qubits [3]. When an LC (L = inductor, C = capacitor) circuit is fabricated using superconducting materials, the energy levels become quantized, so we can control a few microwave photons inside the resonator. By initiating an interaction between the microwave resonator and the superconducting qubits, we can generate an entanglement between the superconducting qubits, where the microwave photons mediate the interaction between them (Fig. 2(a)) [4]. Thus, it is important to achieve strong coupling between the superconducting flux qubit and the microwave resonator. One way to increase the coupling strength between the superconducting qubits and the microwave resonator is to use collective quantum effects*5. By fabricating multiple superconducting flux qubits near the microwave resonator, the superconducting flux qubits show wave-like properties. The collective effect is one such property. This means that by coupling L superconducting qubits with the microwave resonator, the coupling strength is enhanced by a factor of L0.5. In fact, 20 superconducting flux qubits were fabricated near a microwave resonator [5], and a frequency shift to indicate such a collective effect was observed in spectroscopic data (Fig. 2(b)). However, to achieve a practical quantum device, we need to increase the number of superconducting flux qubits collectively coupled with the resonator, which is important to create a large entanglement between the superconducting flux qubits.
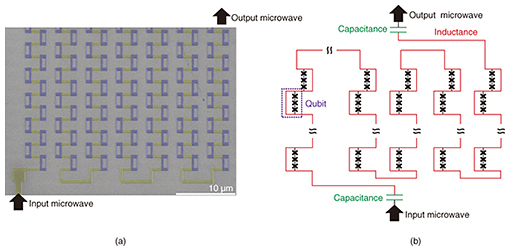
We fabricated a device consisting of 4300 superconducting flux qubits embedded in a microwave resonator (Fig. 3) [6]. By spectroscopically analyzing this device, we observed the enhancement of the coupling strength due to the collective effect between the superconducting flux qubits and the microwave resonator. This represents the largest number of coupled superconducting qubits realized so far and is a crucial step to realize a large entanglement between superconducting qubits.
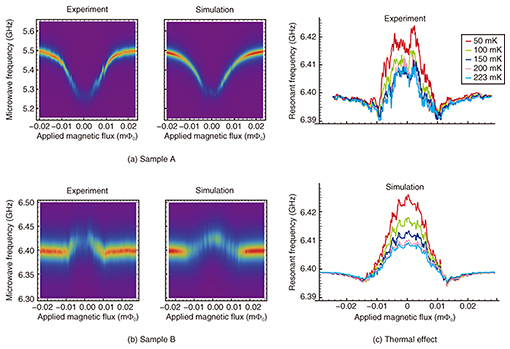
4. Spectroscopic measurements of the microwave resonator transmission propertiesWe placed our sample (sample A) in a dilution refrigerator operating at 20 mK and conducted spectroscopic measurements of the microwave resonator’s transmission properties. By changing the applied magnetic fields so they were perpendicular to the flux qubits, we observed a frequency shift of approximately 250 MHz (Fig. 4(a)). Such a frequency shift is observed due to the collective coupling between the superconducting qubits and the microwave resonator when the resonant frequencies between them are detuned (Fig. 2(b)). We succeeded in reproducing these experimental results using a simple theoretical model that includes collective coupling. We can infer from our numerical simulations that thousands of flux qubits were collectively coupled with the microwave resonator in our experiment. Next, by using the second sample (sample B) fabricated using different qubit conditions, we observed both positive and negative frequency shifts of tens of megahertz. These frequency shifts are known to occur when the tunneling energy of the superconducting flux qubit is smaller than the energy of the microwave resonator (Fig. 2(b)). The observed frequency shift of sample B is one order of magnitude smaller than that of sample A (Fig. 4(b)). This is due to the fact that the tunneling energy of sample B is comparable to the thermal energy of the environment, and the thermal effect suppresses the collective enhancement of the coupling strength. By including the effect of the temperature, we succeeded in reproducing our experimental results with numerical simulations. We measured the temperature dependence of the resonator frequency (Fig. 4(c)) and confirmed that an increase in the temperature suppressed the frequency shift of the resonator. Our results confirm that we can control the strength of the collective coupling by changing the temperature.
5. ConclusionWe fabricated 4300 superconducting flux qubits embedded in a microwave resonator and achieved coherent coupling between them. We observed a large frequency shift of the resonator, indicating collective quantum behavior of the superconducting qubits. It is worth mentioning that we could not observe vacuum Rabi splitting*6 that is an indication of strong coupling between the two systems. With the existing technology, we cannot fabricate homogeneous superconducting flux qubits, so the inhomogeneous resonant frequency of the qubits makes it difficult to observe the vacuum Rabi splitting. To address this problem, it is not possible to create a large entanglement between the qubits for the quantum enhanced magnetic field sensor in the current device. One way to overcome the problem of the inhomogeneous broadening is to fabricate control lines to apply magnetic flux on the qubits, which would enable us to tune the resonant frequency of each qubit. Therefore, as a next step, we aim to achieve strong coupling between the superconducting flux qubits and a microwave resonator by tuning the frequency of the qubits. We will also attempt to generate a large entanglement between the qubits via the microwave resonator, which is useful for constructing an ultrasensitive magnetic field sensor.
References
|
|||||||||||||||||||||||||