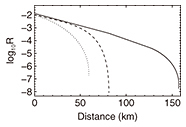
Implementation Security of Quantum Key Distribution

1. Introduction

We often rely on data encryption when sending confidential information such as passwords or private information over the Internet. Modern cryptography is commonly used for this, and with such cryptography, we exploit the fact that it is difficult to solve particular mathematical problems such as the factorization of large numbers by means of existing technologies and algorithms. A crucial problem is that there is no guarantee that these problems are indeed hard to solve. This implies that the security of modern cryptography would be threatened by the development of new algorithms and the technologies to run them.

Researchers have recently been working on new forms of cryptography to protect confidential information sent over a communication channel. These use the laws of nature (such as the properties of a photon) and are called quantum cryptography. In this article, we discuss quantum key distribution (QKD), a particular type of quantum cryptography. One of the remarkable features of QKD is that it is secure against any possible eavesdropping. This is because one has to break the laws of nature to crack QKD, which is of course impossible. Therefore, unlike other modern forms of cryptography, QKD is secure against current eavesdropping technologies and will remain secure against all future technologies.

Optical communications technologies can be utilized in QKD since QKD is part of the optical communications family. However, we need to consider how to generate, manipulate, and detect a single photon, which is far beyond the capabilities of the technologies used in standard optical communications. Research and development of technologies for these tasks has resulted in the commercialization of a QKD system [1], and organizations in several countries, including Japan [2], have started field testing it [3] to determine how it can be integrated with current technologies.

2. Security of QKD

An Internet search for “hacking, QKD” will lead to a number of articles about the successful hacking of QKD. These articles contradict what is mentioned in this article, and to determine what is happening, we need to give a more precise argument about the security of QKD. First, a theory called the security proof of QKD guarantees the security of QKD. When we work on a security proof, we use mathematical models for QKD devices, which are constructed by making assumptions on actual devices. We then apply quantum mechanics and information theory based on these models to create a security argument. For instance, we typically assume that a phase modulator can achieve exact phase modulations of 0, π/2, π, and 3π/2. Quantum key distribution is shown to be secure under such an assumption, but this security statement cannot be applied in practice because the exact modulation cannot be achieved due to noise or imperfections. In other words, the security proof provides us with a conditional statement such as “If a QKD device satisfies these assumptions, then it is secure.” A security proof does not tell us anything about what has to be done to satisfy all the assumptions. Therefore, when some assumptions do not hold, the security argument fails, allowing a hacker to crack QKD systems. This is exactly what is happening in the aforementioned articles found on the Internet. In other words, one cannot crack QKD when all the underlying assumptions hold, but one can crack it by exploiting the gap between the assumptions made in theory and the actual properties of QKD devices.

Therefore, to guarantee the implementation security of QKD, that is, the security of QKD when it is implemented, we need to bridge this gap. There are two approaches for this: (1) developing QKD devices that fulfill all the assumptions, and (2) developing a security proof that accommodates the imperfections of actual QKD devices. Researchers are working on both of these. We have mainly taken the latter approach, which is briefly introduced below.

3. Guaranteeing implementation security of QKD

There are three main components in QKD: a sending device, a quantum channel, and a receiving device, all of which need to be properly implemented in a QKD experiment. When we conduct a security analysis of QKD for a quantum channel, we assume a worst-case scenario in which a quantum channel is totally under the control of an eavesdropper. This scenario includes a case in which an eavesdropper sneakily replaces a noisy and lossy quantum channel with one without any noise and loss, and all the eavesdropping attempts are disguised, as they are mistaken for noise and loss. Therefore, although a quantum channel may be useful to increase the communication speed, it does not provide any advantage in terms of security.

To improve security, therefore, we have to seriously investigate the sending and receiving devices. We discuss here the imperfections of a phase modulator as an example of a sending device. As we mentioned above, with some security proofs, exact phase modulation is assumed. Unfortunately, such an assumption is difficult to satisfy in reality. There is a security proof accommodating such imperfections [4]; however, according to this security proof, a slight degradation in the modulation precision severely limits the communication distance, as shown in Fig. 1. This figure shows the distance (km) dependency of the communication speed in log scale. As can be seen in this figure, just a slight modulation error, such as those of 3.6 and 7.2 degrees, reduces the communication distance significantly. For instance, an error of 3.6 degree halves the achievable communication distance compared to perfect phase modulation.

Fig. 1. Distance dependency of communication speed (R) on a log scale. Solid, dashed, and dotted lines respectively represent cases with perfect phase modulation, a 3.6-degree modulation error, and a 7.2-degree modulation error.

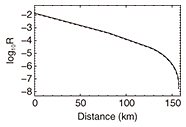
To solve this problem, we checked all the steps in a QKD protocol and found that some data, which were believed to be useless and were thus discarded, were actually the key to solving the problem. We previously proposed a data-processing scheme to enable us to make full use of the data and successfully solved this problem [5]. The graph in Fig. 2 shows the distance (km) dependency of the communication speed based on the same experimental setup as in Fig. 1, but where its data processing was based on our scheme. The three lines are almost superposed, meaning that phase-modulation error was not an issue.

Fig. 2. Distance dependency of R of our scheme on a log scale. Here also, the solid, dashed, and dotted lines respectively represent cases with perfect phase modulation, a 3.6-degree modulation error, and a 7.2-degree modulation error.

So far, the discussion here has focused only on the effect that manipulation with low precision has on security, where an eavesdropper would exploit deviations of an imperfect photon from the ideal photon. Unfortunately, there is another type of eavesdropping strategy in which an eavesdropper actively tries to obtain information that is processed within a QKD device. In this case, an eavesdropper shines a very bright pulse into a QKD device and learns the internal state of the device by monitoring the back-reflected light.

This type of eavesdropping seems to be circumvented by preventing illegitimate pulses from entering a QKD device. This may be possible by installing an optical isolator in front of the QKD device. However, no optical isolator can perfectly extinguish the incoming illegitimate pulses, and we have to seriously consider how to accommodate these attacks in a security proof. In our attempts to do so, we noticed that QKD under this type of attack can be seen as QKD with a multi-mode pulse. We therefore generalized this idea to construct a security proof that was valid against any attack for any given mathematical model of a sending device [6]. This security proof is general in the sense that we do not need to redo a security proof every time we find a new attack, and we are hoping that our security proof will play a key role in guaranteeing security when implementing QKD.

4. Future prospects

Although only a sending device was discussed here, we have seen rapid progress on the receiving-device side as well (see [3] for a recent review of QKD). We expect that it will not be long until we establish practical ultimate security of QKD. We will continue to conduct research to make this a reality.

References

Kiyoshi Tamaki Professor, Faculty of Engineering, University of Toyama. He received an M.Sc. and diploma in theoretical physics from Tokyo Institute of Technology in 1999 and 2001, and a Ph.D. from the Graduate University for Advanced Studies (SOKENDAI) in 2004. During his Ph.D. studies, he spent six months as a visiting researcher with Prof. Norbert Luetkenhaus’s group at the University of Erlangen-Nuremberg, Germany. He also worked at the Perimeter Institute for Theoretical Physics in Canada under Dr. Daniel Gottesman and at the University of Toronto as a postdoctoral fellow with Prof. Hoi-Kwong Lo. He joined NTT Basic Research Laboratories in 2006. He has been a professor in the Faculty of Engineering at the University of Toyama since April 2017.