Synthesizing Ghost-free Stereoscopic Images for Viewers without 3D Glasses

1. Introduction

In standard three-dimensional (3D) stereoscopic displays, a stereo pair (a pair of images each representing a view from each eye position) is simultaneously presented on the same screen. For viewers wearing 3D glasses, an image for the left eye and an image for the right eye are separately presented to the corresponding eyes, and viewers can enjoy 3D depth impressions due to binocular disparity (small differences between the image pair). For viewers who unfortunately watch the display without 3D glasses, however, the superposition of the left and right images produces uncomfortable image blurs and bleeding, which are referred to as ghosts in this article.

Stereoscopic ghosts, caused by the binocular disparity between the stereo image pair, seriously limit the utility of the standard 3D display. In particular, ghosts make the display unsuitable in situations where the same screen is viewed by a heterogeneous group of people, including those who are not supplied with stereo glasses or who have poor stereopsis (the perception of depth produced by the reception in the brain of visual stimuli from both eyes in combination).

2. Stereo image synthesis to achieve perfect backward compatibility

We recently proposed a method to synthesize completely ghost-free stereoscopic images [1]. Our technique gives binocular disparity to a 2D image by the addition of a quadrature-phase pattern that induces spatial subband phase shifts (Fig. 1). The patterns added to the left and right images, which we call disparity inducers, are identical except that they are opposite in contrast polarity. Physical fusion of the two images cancels out the disparity-inducer components and brings the image back to the original 2D pattern (Fig. 2). This is how binocular disparity is hidden from viewers without glasses but remains visible to viewers with them.

Fig. 1. Schematic of how our method cancels stereo ghosts for viewers without 3D glasses.

Fig. 2. Comparison of image quality when viewed without 3D glasses.

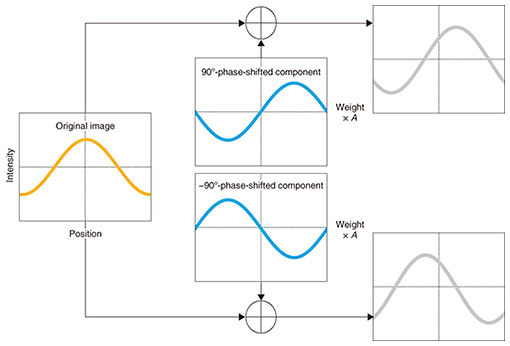
3. Technical details

Our method synthesizes a stereo image by linearly adding a disparity inducer. To realize this process, we manipulate binocular disparity based on a local phase shift. For the sake of simplicity, let us assume a vertical grating whose intensity profile is a sinusoidal wave to be an original image. We use a quadrature (half-cycle)-phase-shifted component of the original image as a disparity inducer (Fig. 3). When the quadrature-phase-shifted component is added to the original image, the resulting composite image is a quarter-cycle-phase-shifted wave from the original one.

Fig. 3. Basic mechanism to produce a relative phase shift.

By contrast, when the quadrature-phase-shifted component is subtracted from the original image, the phase of the original wave is shifted in the opposite direction by a quarter cycle. This phase difference between the resulting images is used as a disparity for producing a depth impression.

Importantly, we can control the size of the phase shift by modulating the amplitude of the quadrature-phase component. Therefore, we can reproduce the desired amount of disparity. The amount of phase shift required to reproduce a specific size of disparity depends on the spatial frequency and the orientation of the original grating. Fusion of the composite images cancels out the effects of the quadrature-phase component and makes the image profile the same as the original one.

4. Application to general images

In general, any arbitrary image can be represented as a combination of sinusoids by a 2D Fourier transform. Thus, the disparity manipulation described above can be easily applied to arbitrary images as long as the disparity for each sinusoidal component is spatially uniform. However, when we want to reproduce a structured map of binocular disparity (disparity map), we need spatially localized information about the spatial frequency and orientation of an input image. To analyze this local structure information, we use the steerable pyramid, which decomposes an image into subband images, each representing local responses tuned to different spatial frequencies and orientations [2].

The process to generate a disparity inducer is as follows: (1) The system first decomposes an input image into subband images using the steerable filters and obtains quadrature-phase-shifted versions of the subband images. (2) The quadrature-phase patterns are weighted so as to reproduce disparity sizes given by an input disparity map. The weight sizes are computed based on the spatial frequency and orientation of each of the quadrature-phase patterns. (3) Finally, the disparity inducer is obtained by reconstructing the weighted quadrature-phase subbands.

There is a huge amount of 3D content in the conventional stereo format. We can also transform that content into our ghost-free format. The most straightforward way to achieve this is to compute a disparity map from a given stereo pair. Then, one can generate a disparity inducer in the same way as described above using one of the stereo images as an original 2D image to which a disparity inducer is added.

However, we present here a more concise way, in which we compute disparity as a phase difference between a given stereo pair and calculate the weight for the quadrature-phase-shifted image directly from the phase difference. When we use the left image of an input stereo pair as an original 2D image to which the disparity is added, the process to generate a disparity inducer is as follows (Fig. 4): (1) The system first decomposes both of the input stereo images into a series of subband images using steerable filters. (2) Then we compute the phase difference between each of the corresponding subband image pairs. (3) From each of the subband images of the left image, we extract the quadrature-phase component. (4) The quadrature-phase patterns are weighted so as to reproduce the phase differences obtained in (2). (5) The disparity inducer is obtained by reconstructing the weighted quadrature-phase subbands. After the disparity inducer is given, the left and right stereo images in our stereo format are respectively generated by the addition/subtraction of the disparity inducer to/from the input left image. By processing every frame in the same manner, we can transform not only static stereo pictures, but also stereo movie sequences into our ghost-free format.

Fig. 4. Process overview to generate a disparity inducer from a standard stereo pair.

The image processing described above is designed so as to effectively drive the binocular mechanisms in our brain. The human visual system analyzes binocular disparity using a bank of multi-scale, orientation-tuned bandpass mechanisms similar to the steerable pyramid. Then the visual system computes the binocular disparity as the phase difference between the corresponding bandpass responses. Therefore, our technique can properly drive the viewer’s binocular vision by adding disparity as a spatial phase shift even though the synthesized stereo images are slightly different from those obtained in the real 3D world.

5. Comparison to previous approach

A previous solution to simultaneously present 3D content and ghost-free 2D content with a single display is to make a special image combination that cancels out, say, the right image component and leaves only the left image to viewers without 3D glasses [3, 4]. However, this method significantly sacrifices the contrast of the original image. In addition, it is incompatible with the standard stereo display system.

Another approach to attenuate stereo ghosts is to compress the magnitude of binocular disparity [5]. This approach is compatible with the standard stereo displays, but it cannot perfectly remove the stereo ghosts.

There is also a stereo-image-synthesis method that is similar to ours [6]. In this method, an edge-enhancing (derivative) filter is used to produce pseudo-disparity. However, this method cannot precisely control the size of disparities since it does not analyze the spatial frequency or orientation of the original image.

Our method can completely remove stereo ghosts while maintaining compatibility with standard stereo display hardware. Unlike the previous solution in which one of the stereo images is entirely canceled out, only the disparity inducer embedded in a stereo image pair is canceled out in our case. Thus, the reduction in the contrast of the original image is moderate or even unnecessary. Moreover, in our method, the size of the phase shift is controlled based on the spatial frequency and orientation of the original image. Therefore, we can easily reproduce natural depth structures that are indistinguishable to the physically correct stereo images.

6. Limitation and future work

In exchange for the ability to present perfect ghost-free 2D images to viewers without glasses, our method has a slightly limited ability to present 3D images compared with the conventional position-shift method. Specifically, there is an upper limit in the disparity magnitude given to the image. Adding a large disparity could affect the dynamic range and induce perceptual artifacts. Thus, when transforming standard stereo images to our ghost-free format, one may have to combine it with a depth compression technique [5].

On the other hand, our method can provide 3D information in a slightly different way from the conventional methods because we can hide disparity information in 2D images. For example, one can use 3D glasses like a loupe to inspect complicated structures of an image on a personal computer monitor while looking at it without glasses otherwise.

In addition, since our technique is based on the linear addition of disparity inducers, when combined with projection mapping, it can add to real objects depth structures that are visible only to viewers with glasses. The projection system can be used, for example, in an art museum to present additional depth impressions onto existing paintings without causing any conflicts with observers who want to appreciate their original appearances.

Finally, our method provides a simple way to linearly decompose a stereo image pair into a single image and a depth pattern (disparity inducer). If the disparity inducer is given, it is easy to transform any 2D content into 3D content. It remains for investigation whether this decomposition contributes to other applications such as effective image data compression.

References

[1]	T. Fukiage, T. Kawabe, and S. Nishida, “Hiding of Phase-based Stereo Disparity for Ghost-free Viewing Without Glasses,” ACM Trans. Graph. (Proc. of SIGGRAPH 2017, Los Angeles, CA, USA), Vol. 36, No. 4, pp. 147:1–17, 2017.
[2]	E. P. Simoncelli and W. T. Freeman, “The Steerable Pyramid: A Flexible Architecture for Multi-scale Derivative Computation,” Proc. of the 2nd IEEE International Conference on Image Processing, Vol. 3, pp. 444–447, Washington, D.C., USA, Oct. 1995.
[3]	W. Fujimura, Y. Koide, R. Songer, T. Hayakawa, A. Shirai, and K. Yanaka, “2x3D: Real Time Shader for Simultaneous 2D/3D Hybrid Theater,” Proc. of SIGGRAPH Asia 2012 Emerging Technologies, pp. 1:1–2, Singapore, Nov./Dec. 2012.
[4]	S. Scher, J. Liu, R. Vaish, P. Gunawardane, and J. Davis, “3D+2DTV: 3D Displays with No Ghosting for Viewers Without Glasses,” ACM Trans. Graph., Vol. 32, No. 3, pp. 21:1–10, 2013.
[5]	P. Didyk, T. Ritschel, E. Eisemann, K. Myszkowski, and H.-P. Seidel, “Apparent Stereo: The Cornsweet Illusion Can Enhance Perceived Depth,” Proc. of SPIE, Vol. 8291, Human Vision and Electronic Imaging XVII, IS&T/SPIE’s Symposium on Electronic Imaging, pp. 1–12, Burlingame, CA, USA, 2012.
[6]	S. Kobayashi, “Image Processing Apparatus, Image Processing Method, and Program,” US Patent, US20100033554A1, 2010.