Transmission of Messages to the Efficiency Limit—Implementation of Tractable Channel Code Achieving the Shannon Limit

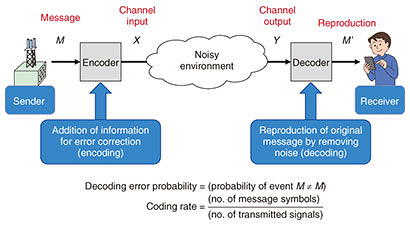
3.1 Communication system achieved using channel codes

A communication system achieved using channel codes is shown in Fig. 1. In this figure, the sender is a wireless station that is sending messages, and the receiver is a user who has a smartphone. The encoder converts a message M to a signal X called a channel input. It is transmitted as a modulated radio wave, where it is assumed that noise is added to the transmission. The decoder converts a reproduction M’ from a received signal Y called a channel output. The transmission is successful when M = M’ is satisfied, and the decoding error probability is defined as the probability of events satisfying M ≠ M’.

Fig. 1. Communication system realized using channel codes.

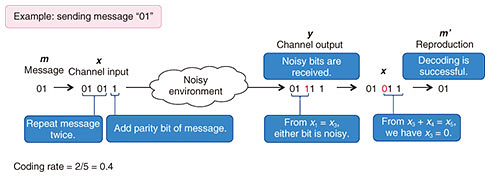
The transmission efficiency, hereafter called the coding rate, is defined as the number of message symbols divided by the number of transmitted signals. A higher coding rate means higher speed transmission. However, a coding rate that is too high makes it impossible to achieve a decoding error probability close to zero. Our goal is to construct an encoder and decoder pair where the decoding error probability is close to zero and the coding rate is close to the fundamental limit.

3.2 Example of channel coding

An example of channel coding of the message “01” is shown in Fig. 2. The encoder converts the message to the channel input signal “01011,” which is a twofold repetition of the message and a 1-bit parity check, which is the sum (exclusive-or) of two message bits. This operation is called encoding. In this example, the decoder observes the channel output signal “01111.” The decoder determines the position of the noise by using the encoding rule and reproduces the original message. This operation is called decoding. In this example, the message is successfully reproduced, but a noisier output may prevent us from reproducing the original message. In Fig. 2, a 2-bit message is encoded in a 5-bit channel input, where the coding rate is 2/5 = 0.4. By increasing the number of repetitions and parity check bits, the number of noisy bits that the decoder can specify is increased while the coding rate is decreased. For high-speed error-free transmission, it is necessary to specify all noisy bits with a probability close to one and obtain the highest possible encoding rate.

Fig. 2. Example of channel coding.

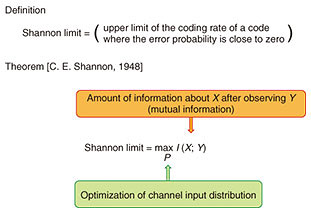
3.3 Shannon limit

The Shannon limit (channel capacity) is defined in Fig. 3. As shown in Fig. 1, the decoding error probability of a code must be close to zero. However, a more efficient code has a higher coding rate. The Shannon limit is the optimum coding rate of codes, where the decoding error probability is close to zero. Shannon derived the limit illustrated in Fig. 3, where the optimum is achievable by letting the number of transmitted signals reach infinity. It is theoretically impossible to construct codes with a rate beyond the Shannon limit. It should be noted that we have to optimize the channel input distribution P, which appears in the maximum operator on the right-hand side of the equality.

Fig. 3. The Shannon limit.

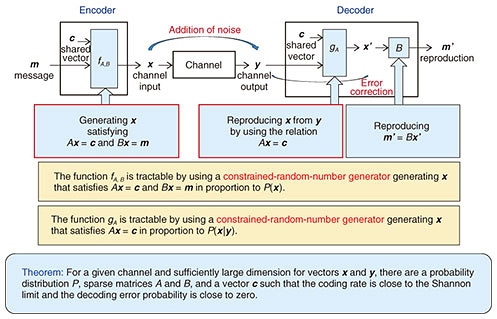
3.4 Proposed method CoCoNuTS

The construction of a channel code using CoCoNuTS is shown in Fig. 4. With the proposed method, a code is constructed by using two sparse matrices (almost all elements of a matrix are zero) A and B, and a vector c. Functions f_A,B and g_A (red squares in Fig. 4) are implemented by using tractable constrained-random-number generators [1–3]. We can achieve the Shannon limit by employing an optimal channel input distribution P.

Fig. 4. Proposed method CoCoNuTS.

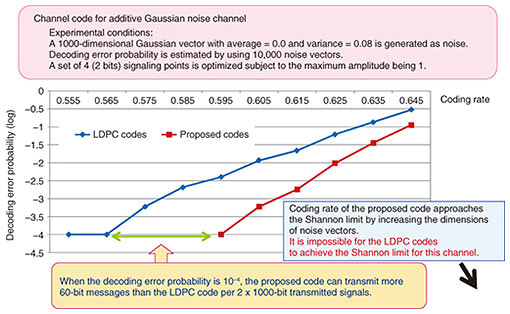
In contrast, a generator matrix is used as the encoder of the conventional LDPC codes, where the channel input distribution is approximately uniform. This implies that the LDPC codes achieve the Shannon limit if the maximum in Fig. 3 is achieved with a uniform input distribution P, and otherwise they cannot achieve the limit.

3.5 Experimental results

In Fig. 5, the proposed codes are compared with the conventional LDPC codes. The horizontal axis represents the coding rate, where a larger value implies better performance. The vertical axis represents the decoding error probability, where a smaller value implies better performance. The graph shows that the proposed codes outperform the LDPC codes. For example, when they are compared on the horizontal line at a decoding error probability of 10⁻⁴, the proposed codes can transmit 60 bits of messages more than the LDPC codes per 2000 bits of transmitted signals.

Fig. 5. Experimental results.

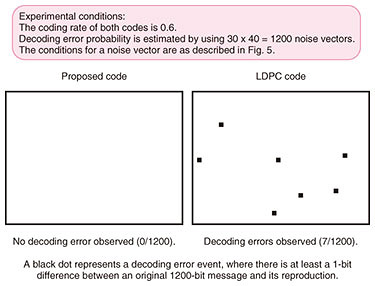
A comparison at the same coding rate of 0.6 is shown in Fig. 6. The black dots represent the decoding error events, where encoding and decoding are repeated 1200 times under the conditions described in Fig. 5. There is no decoding error event with the proposed code, while there are seven decoding error events with the LDPC code. This result suggests that the proposed code is more reliable than the conventional code in the same noisy environment and with the same coding rate.

Fig. 6. Visualization of decoding error events at a coding rate of 0.6.

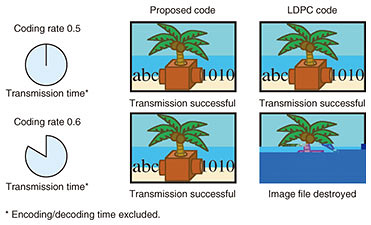
A comparison when a compressed image file (JPEG)^*4 is transmitted, where it is assumed that there is no decoding error, is shown in Fig. 7. In this situation, a decoding error destroys the file, and most of the original image cannot be reproduced. When the coding rate is 0.5, both the proposed code and the LDPC code can reproduce the original image. However, the LDPC code cannot reproduce the original image at a coding rate of 0.6. This implies that the coding rate limit of the LDPC code is between 0.5 and 0.6, which is less than that of the proposed code.

Fig. 7. Transmission of compressed image at a coding rate of 0.6.