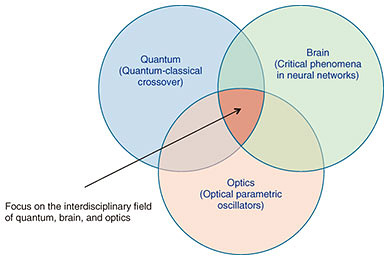
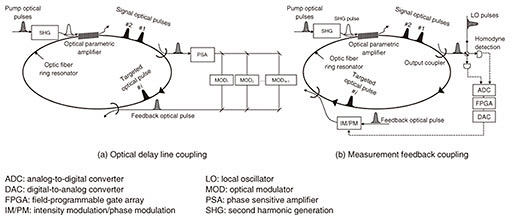
Mission of Physics & Informatics Laboratories

1. Quantum neural networks using optical parametric oscillators

The development of new oscillators for generating coherent electromagnetic waves and the expansion of their application fields has a history marked by a rivalry between oscillators based on two different principles. In electrical engineering terms, one is a negative-resistance oscillator requiring no pump-source coherence, and the other is a nonlinear reactance oscillator requiring coherent pump waves. The development of oscillators for various frequency bands began with the emergence of negative-resistance oscillators that are easy to achieve. This was followed by the development of nonlinear reactance oscillators that generate a coherent wave with less noise.

The development of optical oscillators covering a broad wavelength band from ultraviolet to infrared is no exception to this historical rivalry. A laser, which is an optical negative-resistance oscillator, was developed in 1960 through the work of Theodore Maiman of Hughes Research Laboratories [1]. This was followed by the development of an optical nonlinear reactance oscillator as an optical parametric oscillator (in particular, an oscillator generating continuous waves for practical use) in 1968 by Stephen Harris and Robert Byer of Stanford University [2].

The foundation of optical communication technology, which blossomed in the 20th century, was the laser, but it is our future vision that the foundation of optical information processing technology of the 21st century will be the optical parametric oscillator. This type of parametric oscillator behaves like an analog device with strong quantum properties in the pump region below an oscillation threshold and like a digital device with strong classical properties in the pump region above the threshold. As described below, future information processing technology will require both quantum computing resources and classical computing resources, and the optical parametric oscillator is practically the only device that can simultaneously achieve this dual quantum-classical nature at room temperature.

We have been researching the neural networks using optical parametric oscillators as neurons and using such a configuration in an attempt to solve combinatorial optimization problems and quantum many-body problems that have posed a challenge to the modern computer [3] (Fig. 1). Regarding another element (synapse connections) making up a neural network, there are two methods of implementing a fully connected neural network in which synapse connections are formed between all neurons (Fig. 2). These methods use N optical parametric oscillator pulses circulating in an optical fiber ring cavity of 1 to 10 km for N neurons instead of using N optical parametric oscillators, a scheme that achieves N defect-free uniform neurons simultaneously within a single cavity [4–6].

Fig. 1. Research fields at Physics & Informatics Laboratories (PHI Labs).

Fig. 2. Neural network configuration based on optical parametric oscillators.

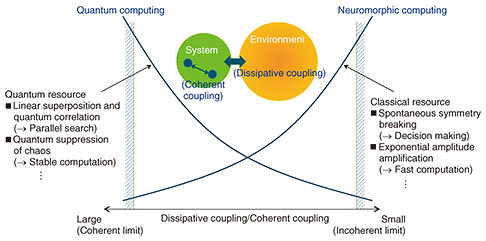
The optical delay line coupling method (Fig. 2(a)) can achieve N (N–1) synapse coupling coefficients [J_ij] through (N–1) optical delay lines and the same number of optical modulators [4]. With this method, (N–1) input pulses j simultaneously couple with a single target pulse i at each time point via coupling coefficient J_ij, so N (N–1) J_ij coefficients are implemented for each round trip to achieve the above for all N target pulses. This method has the advantage of simplifying the implementation of synapse coupling having directionality (J_ij ≠ J_ji).

The measurement feedback coupling method (Fig. 2(b)), on the other hand, can achieve N (N–1) all-synapse coupling with just a single measurement feedback circuit [5, 6]. The former method is thought to be applicable to the implementation of large-scale, high-speed, and sparsely coupled neural networks and to quantum many-body problems. The latter method, however, is thought to be applicable to the implementation of medium-scale, high-order nonlinear coupling and densely coupled neural networks and to combinatorial optimization problems.

2. Application fields

This section introduces the application fields envisioned for quantum neural networks using optical parametric oscillators.

3. Quantum-classical crossover physics

The quantum-classical crossover problem refers to the question of when and how quantum theory, which has been successful in describing the microscopic world, crosses over into classical theory, which rules over the macroscopic world. This question is the most fundamental theme for quantum physicists. One theoretical model that can make this problem easy to understand is an open system in which a system having a few degrees of freedom couples with an environment having many (or infinite) degrees of freedom [14]. As shown in Fig. 3, as dissipative coupling between the system and environment (decoherence) becomes smaller compared with the strength of coherent coupling within the system, quantum computing resources become more effective, such as quantum parallel search using linear superposition and quantum suppression of classical chaos using quantum interference. For this reason, it has been thought up to now that a quantum computer should be developed in a region that makes dissipative coupling with the environment as small as possible. Concepts such as quantum error correcting codes and topological quantum computers have emerged along this line of thinking.

Fig. 3. Computing with quantum and classical resources.

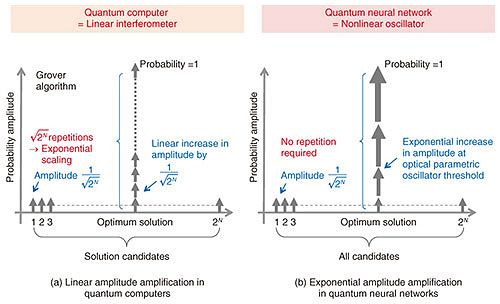
As dissipative coupling with the environment becomes larger, however, there is an increase in the effectiveness of classical computing resources, such as irreversible decision making of a final solution by spontaneous symmetry breaking and exponential amplification of the amplitude of the selected final solution, as stable classical information. It has therefore been thought that a neuromorphic computer that mimics the function and mechanism of human nerve cells or acquires ideas based on human ways of thinking should be developed in a robust classical region that would make dissipative coupling with the environment as large as possible and completely remove quantum coherence in the system.

We consider that the computer of the future should be developed specifically in this quantum-classical crossover region in which the two types of computing resources—quantum and classical—can be used simultaneously. An optical parametric oscillator network is a unique hardware solution that can freely move about this quantum-classical crossover region by adjusting the pump rate. This approach has something in common with recent thinking by neuroscientists known as “computing at criticality” in which advanced functions of the human brain (consciousness, cognition, and decision-making) are based on types of phase transitions and critical phenomena in a massive neural network [15].

4. Why are classical computing resources also necessary?

A method for solving combinatorial optimization problems using only quantum computing resources is shown in Fig. 4(a). This method first expresses all (2^N) candidates of the solution of a given problem as linear superposition states, each having the same probability amplitude (1/). Then, after identifying the optimal solution by some methods such as the phase estimation algorithm, it amplifies the amplitude of that particular state from 1/ to 1 and attenuates the amplitudes of all other states from 1/ to 0. Finally, by conducting projective measurements of 0 or 1 against N quantum bits, it determines an optimal solution with a probability close to 100%. The bottleneck with this method lies in how to amplify the amplitude of the optimal solution and how to attenuate the amplitudes of all other states that are not an optimal solution.

An optimal method for achieving this goal using a quantum computer was discovered by L. K. Grover [16]. Repeating this routine called Grover iteration a total of times obtains the above final state. This means that exponential time must be spent in solving a combinatorial optimization problem using a quantum computer. The theoretical limits of the computational time needed to complete this Grover iteration for problem sizes of N = 20, 50, 100, and 150 bits are 4 x 10⁻³ s, 6 x 10² s, 2 x 10¹⁰ s, and 6 x 10¹⁷ s. It is assumed that there is no decoherence and no gate error, and consequently no need for using quantum error correcting codes, and that fully connected bits are implemented so that non-localized two-bit gates can be freely implemented at a high speed of 1 ns. It is also assumed that the optimal solution to a given problem can be identified instantaneously by a new and independent algorithm, which is yet to be discovered. Yet, even with such an idealized quantum computer, the above result shows that it would take about 20 billion years to amplify the probability amplitude of the optimal solution from 1/ to 1 for an extremely small problem of N = 150 bits.

What would be the computational time for solving the same type of problem with a coherent Ising machine? As shown in Fig. 4(b), since N optical parametric oscillator pulses below the oscillation threshold are in 0-phase and π-phase linear superposition states, all solution candidates can be expressed as linear superposition states, each having the same probability amplitudes (1/) in the same manner as the quantum computer. At this time, if the pump rate is increased to the oscillation threshold, the optimal solution having minimum network loss gives rise to single-mode oscillation, and that amplitude is exponentially amplified from its initial value (1/) to its final value (1) in a time comparable to a photon lifetime (on the order of μs–ms) at most [3]. This exponential amplification is a characteristic phenomenon in a classical (open) system that cannot be achieved in a quantum system. The computational times (experimental results) for obtaining optimal solutions to the same combinatorial optimization problem (Ising model) with a coherent Ising machine are 1.0 x 10⁻⁴ s, 3.7 x 10⁻⁴ s, 2.5 x 10⁻³ s, and 5.4 x 10⁻² s [7].

Fig. 4. Two computational methods for combinatorial optimization problems.

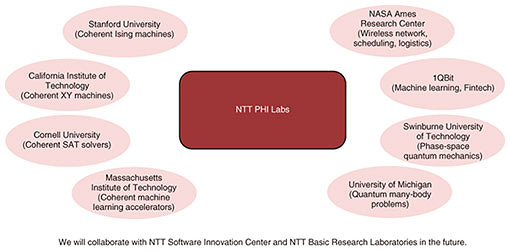
With the exception of special problems having hidden periodicity (factorization, discrete logarithm, etc.), this example shows that classical computing resources, such as exponential amplitude amplification, will be essential to future computers for solving general combinatorial optimization problems at high speed in addition to quantum computing resources in the manner of linear superposition.

We emphasize that a quantum computing based on Grover iteration is an exact solver while a coherent Ising machine is a heuristic solver, for which the theoretical upper bound of computation time is not established for coherent Ising machines yet.

5. Research partners

The development of quantum neural networks using optical parametric oscillators targeting combinatorial optimization problems and quantum many-body problems is moving forward at NTT. PHI Labs is actively promoting joint research with outside research institutions to fulfill its responsibility of searching out new concepts and principles (Fig. 5).

Fig. 5. PHI Labs and its partners.

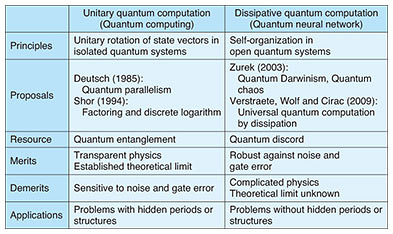
The left side of the research partner diagram in Fig. 5 consists mainly of the experimental group. The Stanford University team (Professor Hideo Mabuchi, Professor Martin Fejer, Associate Professor Benjamin Lev, Associate Professor Surya Ganguli, Assistant Professor Amir Safavi-Naeini) is researching coherent Ising machines based on optical or superconducting parametric oscillator networks and critical phenomena in neural networks. The Cornell University team (Assistant Professor Peter McMahon) is researching coherent SAT solvers based on recurrent optical parametric oscillator networks. The California Institute of Technology team (Assistant Professor Alireza Marandi) is researching coherent XY machines based on non-degenerate optical parametric oscillator networks. The Massachusetts Institute of Technology team (Associate Professor Dirk Englund, Professor William Oliver) is researching coherent accelerators (targeting deep machine learning) based on optical homodyne mixers and also fabrication of superconducting parametric oscillator networks.

The right side of the research partner diagram in Fig. 5 consists of the theoretical group. The NASA Ames Research Center team (Quantum Artificial Intelligence Laboratory: QuAIL Lead Eleanor Rieffel) is researching application algorithms for wireless networks, scheduling, logistics, and other areas. The 1QBit team (Group Head Pooya Ronagh) is researching application algorithms for machine learning. The Swinburne University of Technology team (Professor Peter Drummond, Professor Margaret Reid) is researching quantum stochastic differential equations by using the phase-space method. The University of Michigan team (Professor Franco Nori) is researching quantum simulations of non-Abelian anyon particles and topological physics.

Finally, Table 1 summarizes the differences between conventional quantum computers and new quantum neural networks that we are researching.

Table 1. Two quantum computational models.

6. Conclusion

The first AT&T-NTT executive meeting took place more than 30 years ago, and meetings were subsequently held annually at an AT&T or NTT research laboratory. At that time, I was one of the members from the NTT laboratories then headed by NTT senior executive vice president Yasusada Kitahara and remember well my visit to Bell Labs in New Jersey. The president of Bell Labs (to whom I was introduced) was British, the vice president in charge of research was German, and the executive director overseeing the physics department was Indian. The director of theoretical physics (commonly known as Physics 001) was American, and it was he who gave the keynote talk at this first AT&T-NTT executive meeting. I cannot forget the reprimand that he received at that time from Dr. Arno Penzias, the vice president of research (and recipient of the 1978 Nobel Prize in Physics), who said “If you speak that fast, you will lose half of your audience in the room!” My dream was to one day make the NTT laboratories into a place with such diversity and caliber—we stood at the starting line of that endeavor.

References

[1]	T. H. Maiman, “Stimulated Optical Radiation in Ruby,” Nature, Vol. 187, pp. 493–494, Aug. 1960.
[2]	R. L. Byer, M. K. Oshman, J. F. Young, and S. E. Harris, “Visible CW Parametric Oscillator,” Appl. Phys. Lett., Vol. 13, No. 3, p. 109, Aug. 1968.
[3]	Z. Wang, A. Marandi, K. Wen, R. L. Byer, and Y. Yamamoto, “Coherent Ising Machine Based on Degenerate Optical Parametric Oscillators,” Phys. Rev. A, Vol. 88, No. 6, 063853, Dec. 2013.
[4]	A. Marandi, Z. Wang, K. Takata, R. L. Byer, and Y. Yamamoto, “Network of Time-multiplexed Optical Parametric Oscillators as a Coherent Ising Machine,” Nat. Photon., Vol. 8, pp. 937–942, Oct. 2014.
[5]	T. Inagaki, Y. Haribara, K. Igarashi, T. Sonobe, S. Tamate, T. Honjo, A. Marandi, P. L. McMahon, T. Umeki, K. Enbutsu, O. Tadanaga, H. Takenouchi, K. Aihara, K. Kawarabayashi, K. Inoue, S. Utsunomiya, and H. Takesue, “A Coherent Ising Machine for 2000-node Optimization Problems,” Science, Vol. 354, No. 6312, pp. 603–606, Nov. 2016.
[6]	P. L. McMahon, A. Marandi, Y. Haribara, R. Hamerly, C. Langrock, S. Tamate, T. Inagaki, H. Takesue, S. Utsunomiya, K. Aihara, R. L. Byer, M. M. Fejer, H. Mabuchi, and Y. Yamamoto, “A Fully Programmable 100-spin Coherent Ising Machine with All-to-all Connections,” Science, Vol. 354, No. 6312, pp. 614–617, Nov. 2016.
[7]	R. Hamerly, T. Inagaki, P. L. McMahon, D. Venturelli, A. Marandi, T. Onodera, E. Ng, C. Langrock, K. Inaba, T. Honjo, K. Enbutsu, T. Umeki, R. Kasahara, S. Utsunomiya, S. Kako, K. Kawarabayashi, R. L. Byer, M. M. Fejer, H. Mabuchi, D. Englund, E. Rieffel, H. Takesue, and Y. Yamamoto, “Experimental Investigation of Performance Differences between Coherent Ising Machines and a Quantum Annealer,” Sci. Adv., Vol. 5, No. 5, eaau0823, May 2019.
[8]	T. Leleu, Y. Yamamoto, P. L. McMahon, and K. Aihara, “Destabilization of Local Minima in Analog Spin Systems by Correction of Amplitude Heterogeneity,” Phys. Rev. Lett., Vol. 122, No. 4, 040607, Feb. 2019.
[9]	Y. Takeda, S. Tamate, Y. Yamamoto, H. Takesue, T. Inagaki, and S. Utsunomiya, “Boltzmann Sampling for an XY Model Using a Non-degenerate Optical Parametric Oscillator Network,” Quantum Sci. Technol., Vol. 3, No. 1, 014004, Nov. 2017.
[10]	M. Ercsey-Ravasz and Z. Toroczkai, “Optimization Hardness as Transient Chaos in an Analog Approach to Constraint Satisfaction,” Nat. Phys., Vol. 7, pp. 966–970, Oct. 2011.
[11]	H. Goto, K. Tatsumura, and A. R. Dixon, “Combinatorial Optimization by Simulating Adiabatic Bifurcations in Nonlinear Hamiltonian Systems,” Sci. Adv., Vol. 5, eaav2372, Apr. 2019.
[12]	R. P. Feynman, “Simulating Physics with Computers,” Int. J. Theoretical Physics, Vol. 21, Nos. 6/7, pp. 467–488, June 1982.
[13]	M. D. Fraser, S. Höfling, and Y. Yamamoto, “Physics and Applications of Exciton–Polariton Lasers,” Nat. Mater., Vol. 15, pp. 1049–1052, Sept. 2016.
[14]	W. H. Zurek, “Decoherence, Einselection, and the Quantum Origins of the Classical,” Rev. Mod. Phys., Vol. 75, No. 3, pp. 715–775, July 2003.
[15]	J. Beggs, “Editorial: Can There Be a Physics of the Brain?”, Phys. Rev. Lett., Vol. 114, No. 22, 220001, June 2015.
[16]	L. K. Grover, “A Fast Quantum Mechanical Algorithm for Database Search,” Proc. of 28th Annual ACM Symposium on the Theory of Computing,” pp. 212–219, Philadelphia, PA, USA, May 1996.