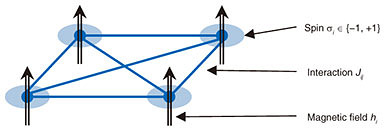
You need Adobe Reader 7.0 or later in order to read PDF files on this site.
If Adobe Reader is not installed on your computer, click the button below and go to the download site.

Feature Articles: Phygital-data-centric Computing for Data-driven Innovation in the Physical World

Vol. 18, No. 1, pp. 35–40, Jan. 2020. https://doi.org/10.53829/ntr202001fa5

LASOLV^TM Computing System: Hybrid Platform for Efficient Combinatorial Optimization

Junya Arai, Satoshi Yagi, Hiroyuki Uchiyama,
Kinya Tomita, Kazuhiro Miyahara, Tokuma Tomoe,
and Keitaro Horikawa

Abstract

LASOLV^TM is a computing machine developed by NTT based on photonics technologies. While we can efficiently solve combinatorial optimization problems by using LASOLV, there are technical challenges in its application to real-world problems. For example, we need to mathematically convert problems to a specific format for solving them using LASOLV. Moreover, LASOLV requires cooperation with conventional digital computers to solve complex problems. In this article, we introduce LASOLV Computing System, which is a computing platform that helps users overcome these challenges.

Keywords: LASOLV, combinatorial optimization, non-von Neumann Computer

1. Challenges in using Ising computers

We are close to the end of Moore’s Law, and it is becoming increasingly difficult to significantly improve computing performance. Nevertheless, we are still facing complex problems that overwhelm today’s conventional digital computers. Combinatorial optimization is one such problem. It asks which answer is the ‘best’ in a set of possible answers, for example, “Which is the shortest route that visits all the given cities?” (traveling salesman problem) and “How can we assign colors to each area using a limited number of colors without assigning the same color to adjacent areas?” (graph coloring problem). We can find these simple questions in real-world problems such as quality improvement of wireless communication. To provide wireless access in a large venue, multiple access points might be installed. Closely located access points should not use the same frequency band; otherwise, wireless access will be unstable due to radiowave interference. We can consider this problem as a graph coloring problem that assigns frequency bands instead of colors. Thus, combinatorial optimization is applied in various real-world problems.

Various instances of combinatorial optimization can be converted into Ising optimization problems, i.e., a ground-state search of the Ising model. The Ising model is a theoretical model in statistical mechanics that represents a network of spins (Fig. 1). Spin σ_i takes one of two states: up (+1) or down (−1). By letting J_ij and h_i represent the strengths of a spin-to-spin interaction and a magnetic field, respectively, the ground state refers to the spin configuration that minimizes the Ising Hamiltonian H defined as

Fig. 1. Ising model.

Computers specialized for Ising optimization have been developed to efficiently solve Ising optimization problems. We call these computers Ising computers. There are several types of Ising computers: quantum annealing machines, such as D-Wave 2000Q, specially designed semiconductor chips, such as Fujitsu’s Digital Annealing Unit, and the coherent Ising machine (CIM) [1]. The CIM is an Ising computer that simulates the Ising model using photonics technologies. NTT Basic Research Laboratories is conducting research and development of LASOLV^TM (Fig. 2), which is a CIM implemented by NTT. Although Ising computers can do nothing other than solve Ising optimization problems of a limited number of spins, we can apply them to complex problems by using hybrid algorithms. Hybrid algorithms use both Ising computers and digital computers cooperatively. For example, decomposition heuristics solves large-scale Ising optimization problems by iteratively generating small subproblems on a digital computer and solving them on an Ising computer. Hence, Ising computers are widely applicable to real-world problems.

Fig. 2. Appearance of LASOLV^TM.

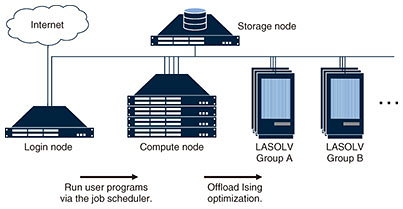
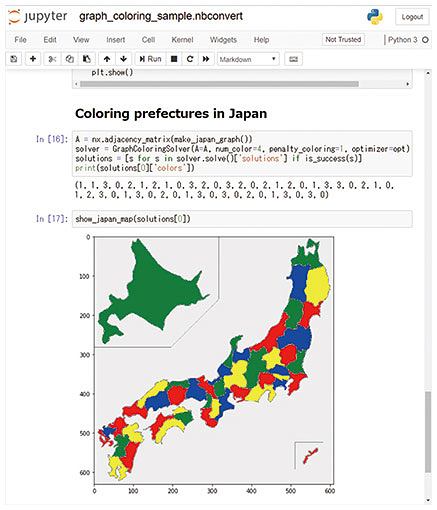
However, there are several challenges with using Ising computers. One of the most fundamental challenges is sharing among multiple users. Since it is difficult to have a ‘personal’ Ising computer due to its cost and facility requirements, we need a multi-user system that coordinates accesses to Ising computers. Some companies solve this problem by using cloud platforms [2, 3] that provide Ising computers as a service. Platform users run their programs on their digital computers and offload Ising optimization to the cloud by issuing a web application programming interface (API) request from the programs. While these platforms enable many developers to use Ising computers, they are inefficient in executing hybrid algorithms. Latencies of web API requests via the Internet are significantly long compared with the solution time of Ising computers, which is in milliseconds. Since hybrid algorithms tend to involve frequent communication between Ising computers and digital computers, communication overheads affect performance. Thus, we are still facing challenges with using Ising computers.

To solve these problems, we developed a platform for Ising computing. In this article, we first clarify the issues with the design of Ising computing platforms then introduce our platform, LASOLV Computing System (LCS). The most distinguishing feature of LCS is the integration of LASOLV and digital computers in a single system. LCS allows users to run their programs on a digital computer co-located with LASOLV. This enables efficient communication between LASOLV and digital computers. LCS also provides a Python library that assists in converting various problems to Ising optimization problems. We give details of LCS in the following sections. Due to space limitations, we omit a description of LASOLV. Refer to a previous article [1] for further details.

2. Issues in platform design

In this section, we state three issues with the design of Ising computing platforms.

2.1 Efficiency

As mentioned above, communication via the Internet takes an order of magnitude longer than Ising optimization. In addition, as technology advances, Ising computers will have a larger number of spins. For example, LASOLV currently supports up to 2000 spins, but NTT Basic Research Laboratories aims to increase this to 100,000 spins. As a result, the data size of Ising optimization problems, that is, the size of J_ij and h_i, will increase, and communication efficiency will have more impact on performance. Therefore, platforms need to be designed to minimize communication overheads.

2.2 Extensibility

Specifications of Ising computers are subject to change due to their evolution. This inevitably makes the platforms a heterogeneous environment consisting of incompatible Ising computers. Thus, it is necessary to manage these computing resources so that users can avoid compatibility problems and effectively use available resources.

2.3 Productivity

Platform users have to convert combinatorial optimization problems into Ising optimization problems to use Ising computers. This conversion requires special skills and knowledge of Ising computers. Since conversion methods differ among problems, it is impractical to provide ready-made conversion algorithms for each problem. To achieve high productivity for a wide range of purposes, we need to design a programming interface that offers both convenience and versatility.

3. LASOLV Computing System

NTT Software Innovation Center has developed LCS, which is a computer cluster with a Python library and middleware such as a job scheduler. It has the following three features to solve the design problems described in the previous section.

3.1 CIM-digital integration

To enable efficient communication between LASOLV and digital computers, they are integrated within a single cluster of LCS (Fig. 3). Except for the integration of LASOLV, this is a cluster configuration standard in high-performance computing. Users can request execution of their program as a job through SSH (Secure Shell) or Jupyter Notebook on web browsers (Fig. 4). Through cooperation of the job scheduler and LCS library, Ising optimization is implicitly offloaded to LASOLV, and the other computation is executed on a compute node using a digital computer. Since compute nodes and LASOLV communicate within the cluster, LCS can provide higher-bandwidth and lower-latency communication than other platforms. In addition, LCS coordinates jobs so that each one can occupy a CPU (central processing unit) core and LASOLV exclusively; thus, multiple users can use LCS simultaneously.

Fig. 3. Configuration of LCS.

Fig. 4. Use of Jupyter Notebook.

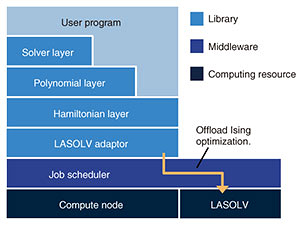
3.2 Group dispatch

LCS is designed to be a scale-out system. Since LASOLV with different specifications may appear in the future, LCS makes groups of compatible LASOLVs for ease of management. Users can select a target group for offloading depending on the requirements of the problem (e.g., the number of spins). LCS then distributes offloading requests among LASOLVs in the target group for using them equally and improving throughput. Note that we are going to update the library for automatically determining the target group for offloading.

3.3 Layered reduction

Combinatorial optimization problems are converted into Ising optimization problems by the following three steps: formally defining the problem, converting it to a minimization problem of a polynomial objective function, and deforming the objective function to the Ising Hamiltonian. To offer options of the programming interface to cover various use cases, the LCS library has the following three layers that correspond to each conversion step (Fig. 5).

Fig. 5. Software and hardware stack of LCS.

(1) Solver layer

The solver layer is a set of problem-specific conversion algorithms for well-known NP-hard problems such as the traveling salesman and graph coloring problems. These algorithms generate a polynomial objective function or the Ising Hamiltonian, which is handled in the following layers.

(2) Polynomial layer

This layer provides an internal domain-specific language (DSL) for converting polynomial objective functions into the Ising Hamiltonian. The DSL is useful when the solver layer lacks an algorithm for the problem to be solved or when users need more flexibility for hand-tuning.

(3) Hamiltonian layer

The Hamiltonian layer is a raw interface for the Ising Hamiltonian. It takes J_ij and h_i as inputs, solves the Ising optimization problem using LASOLV, and returns the answer.

While the solver layer has an algorithm for the graph coloring problem, we solve it using the DSL of the polynomial layer as an example. Consider the graph coloring problem that asks how we can paint n vertices in graph G using c colors so that adjacent vertices have different colors. By letting A be an adjacency matrix of G and p be a hyperparameter and using the variable x_v,i ∈ {0, 1}, we can convert the graph coloring problem into the minimization problem of the following function [4]:

This function is quadratic polynomial about x_v,i. Using the DSL of the polynomial layer, this function can be expressed and minimized using intuitive Python code (Fig. 6).

Fig. 6. Sample code of the polynomial layer.

Moreover, the Hamiltonian layer provides a hybrid algorithm for solving large-scale Ising optimization problems beyond the capacity of LASOLV. This is a heuristics we developed based on several existing methods.

To deliver our research and development outcomes, such as this heuristics, to users quickly, we developed an original library with which users can benefit from these outcomes by simply implementing programs. Users can also use other libraries [5–8] at the same time for Ising computing on LCS. These libraries finally generate the Ising Hamiltonian; thus, it can be solved by the Hamiltonian layer. Conversely, results of Ising conversion using the LCS library can be used as input for Ising computers other than LASOLV.

4. Future prospects

In this article, we first stated issues with the design of Ising computing platforms then introduced how LCS solves them.

LCS is currently available to research collaborators in the small-start configuration of two high-end servers that serve as a login, compute, and storage node and one LASOLV. To promote research and development using LASOLV, we will continue to improve LCS.

References

[1]	H. Takesue, T. Inagaki, K. Inaba, and T. Honjo, “Quantum Neural Network for Solving Complex Combinatorial Optimization Problems,” NTT Technical Review, Vol. 15, No. 7, 2017. https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr201707fa2.html
[2]	D-Wave Leap, https://cloud.dwavesys.com/leap/
[3]	Fujitsu Digital Annealer, https://www.fujitsu.com/global/digitalannealer/services/
[4]	A. Lucas, “Ising Formulations of Many NP Problems,” Front. Phys., Vol. 2, 2014.
[5]	Wildqat, https://github.com/Blueqat/Wildqat
[6]	D-Wave’s Ocean software, https://ocean.dwavesys.com/
[7]	OpenJij, https://github.com/OpenJij/OpenJij
[8]	PyQUBO, https://github.com/recruit-communications/pyqubo

Trademark notes

All brand, product, and company/organization names that appear in this article are trademarks or registered trademarks of their respective owners.

	Junya Arai Researcher, Distributed Computing Technology Project, NTT Software Innovation Center. He received a Bachelor of Science and a Master of Information Science and Technology from the University of Tokyo in 2011 and 2013 and a Ph.D. in information science from Osaka University in 2019. He joined NTT in 2013 and has been studying efficient graph algorithms, parallel distributed computing, and development and operation of computer clusters. He is a member of the Association for Computing Machinery and the Database Society of Japan.
	Satoshi Yagi Senior Research Engineer, Distributed Computing Technology Project, NTT Software Innovation Center. He received a B.E. and M.E. from Waseda University, Tokyo, in 2000 and 2002. He joined NTT Information Sharing Platform Laboratories in 2002. Since then, he has been studying digital identity, data mining, and optimization problems.
	Hiroyuki Uchiyama Senior Research Engineer, Distributed Computing Technology Project, NTT Software Innovation Center. He received a B.E. and M.E. in systems science and applied informatics from Osaka University in 2000 and 2002. He joined NTT Cyber Space Laboratories in 2002 and investigated XML filter engines and distributed stream processing. From 2008 to 2014, he was a member of the commercial development project of the distributed key-value store and distributed SQL query engine. He is currently investigating a high-speed transaction engine, LASOLV Computing System, and optimization of hybrid online analytical processing and machine learning.
	Kinya Tomita Research Engineer, Distributed Computing Technology Project, NTT Software Innovation Center. He received a B.S. and M.S. in applied chemistry from Keio University, Kanagawa, in 1987 and 1989. He joined NTT Communications and Information Processing Laboratories in 1989 and studied operator service support technology and the practical use of an operator support system. He then joined NTT Software in 1996 and worked in software sales, system integration, and software development. He then joined NTT Communications in 2000 and worked in web service software design, network business system engineering (SE), and SE project management. He joined NTT Network Operation Laboratory Information and Communication Systems Laboratories in 2009 and investigated the practical use of common systems. He joined NTT Software Innovation Center in 2018 and is investigating cloud system SE and LASOLV Computing System.
	Kazuhiro Miyahara Researcher, IoT Framework SE Project, NTT Software Innovation Center. He received a B.S. in mathematics and M.E. in information science and technology from Waseda University, Tokyo, in 2012 and 2014. He joined NTT Software Innovation Center in 2014. He has been engaged in research and development of distributed object storage software (OpenStack Swift). He is currently working on Axispot^TM, a distributed spatio-temporal database management technology, specifically on developing new functions such as geometrical search and flexible search, and LASOLV, specifically on constructing mathematical models for practical problems.
	Tokuma Tomoe Researcher, Distributed Computing Technology Project, NTT Software Innovation Center. She received a B.E. in electrical engineering from Shanghai University in 2013 and an M.E. in electrical computer engineering from Yokohama National University, Kanagawa, in 2019. She is currently studying combinatorial optimization and machine learning.
	Keitaro Horikawa Senior Research Engineer Supervisor, Distributed Computing Technology Project, NTT Software Innovation Center. He received a B.E. and M.E. in information engineering from Niigata University in 1988 and 1990. He joined NTT Software Laboratories in 1990 and received the best paper award for young researchers from the Information Processing Society of Japan. He also has PMP (Project Management Professional) and TOGAF 9 certification. He graduated from the MOT (Management of Technology) course of Japan Productivity Center. His research interests include software design, distributed object computing, metaprogramming, and computational reflection. He has recently been involved in optimization programming and data analysis processing using lightweight programming languages.