
You need Adobe Reader 7.0 or later in order to read PDF files on this site.
If Adobe Reader is not installed on your computer, click the button below and go to the download site.

|
Feature Articles: Toward New-principle Computers
Vol. 19, No. 5, pp. 23–28, May 2021. https://doi.org/10.53829/ntr202105fa3
A Long-lived Tunable Qubit for Bosonic Quantum Computing
Leonid V. Abdurakhimov, Imran Mahboob, Hiraku Toida,
Kosuke Kakuyanagi, and Shiro Saito
Abstract
This article reviews a recent experiment that demonstrated a new hybrid type of tunable superconducting qubit consisting of a two-dimensional (2D) superconducting capacitively shunted flux qubit coupled to a 3D microwave cavity. Such a 3D hybrid flux qubit has extremely long relaxation times, which are comparable to or exceed the best values reported for 2D flux qubits. This new design of frequency-tunable qubits is uniquely suited for applications in bosonic quantum computing, which exploits multiphoton states of 3D microwave cavities.
Keywords: superconducting flux qubit, 3D microwave cavity, quantum computation
1. Introduction
Quantum computation is a new computing paradigm based on well-studied, but not yet fully exploited, quantum phenomena such as superposition and entanglement. The key element of a quantum computer is a qubit: a two-level system that can be prepared in an arbitrary state |ψ described by a linear combination (superposition) of qubit pure states 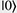 and and 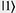 (i.e., (i.e., 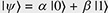 , where α and β are complex amplitudes). The number of computational basis states of a system of N qubits scales with the number of qubits as 2N. For example, a state of a two-qubit system can be described by a superposition of 22 = 4 states (i.e., , where α and β are complex amplitudes). The number of computational basis states of a system of N qubits scales with the number of qubits as 2N. For example, a state of a two-qubit system can be described by a superposition of 22 = 4 states (i.e., 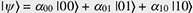 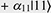 ). Some multi-qubit states can be represented as a product of individual qubit states: for example, the state of two qubits A and B ). Some multi-qubit states can be represented as a product of individual qubit states: for example, the state of two qubits A and B 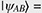 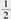 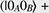 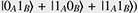 can be decomposed to the product of the states of A and B can be decomposed to the product of the states of A and B 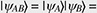 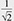 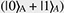 ¡ß ¡ß 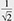 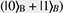 . Other multi-qubit quantum states—so-called entangled states—cannot be obtained by multiplication of single qubit states, for example, the two-qubit state . Other multi-qubit quantum states—so-called entangled states—cannot be obtained by multiplication of single qubit states, for example, the two-qubit state 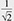  . By using superposition and entanglement phenomena, information from many qubits can be simultaneously encoded in a single quantum state. Quantum algorithms, such as Shor’s algorithm for integer factorization and Grover’s search algorithm, use this property of quantum systems (quantum parallelism) to encode different function instances (different function realizations) in a single quantum state and compute their outcomes at once. A sufficiently large quantum computer will be able to solve a number of numerical problems, such as integer factorization and database search, much faster than conventional computers. . By using superposition and entanglement phenomena, information from many qubits can be simultaneously encoded in a single quantum state. Quantum algorithms, such as Shor’s algorithm for integer factorization and Grover’s search algorithm, use this property of quantum systems (quantum parallelism) to encode different function instances (different function realizations) in a single quantum state and compute their outcomes at once. A sufficiently large quantum computer will be able to solve a number of numerical problems, such as integer factorization and database search, much faster than conventional computers.
Several hardware platforms for quantum computing are being actively studied, including superconducting qubits, trapped ions, optical photonic systems, and spin qubits. Although the above hardware platforms have their own unique advantages and disadvantages, superconducting qubits is arguably the most advanced hardware platform for quantum computing, which is pursued by tech giants such as Google, IBM, and Microsoft, as well as new startups such as Rigetti Computing.
There are many types of superconducting qubits, but one particular variation (the so-called transmon) has become prevalent. Transmons can be roughly separated into two large groups: fixed-frequency and tunable qubits. Fixed-frequency qubits generally demonstrate better coherence times, while tunable qubits provide more freedom in terms of possible quantum protocols. In the most advanced superconducting qubit platforms, both fixed-frequency qubits (IBM, Yale University) and tunable qubits (Google, Delft University) are used (Table 1).

Table 1. The comparison table of currently the most advanced superconducting qubit platforms. (a) Values in the brackets are coherence times of the 2D transmon (ancilla) qubit. Data are taken from F. Arute et al. [1], E. J. Zhang et al. [2], M. A. Rol et al. [3], and N. Ofek et al. [4].
Despite the recent impressive progress in building small-scale superconducting qubit systems, development of a universal quantum computer is still a very challenging task. The major obstacle is the loss of quantum information due to the interaction with noisy environments. For single qubit operations, the important figures of merit are energy-relaxation time T1 and dephasing time T2. In systems, in which quantum information is encoded directly into physical qubits (Google, IBM and Delft University systems), typical T1 and T2 values are in the range of 100 µs (Table 1), while characteristic qubit manipulation times are on the order of 100 ns. Therefore, error rates in state-of-the-art systems are on the order of p ≈ 10−3. To execute reliable quantum computations at such error rates, implementation of error-correction algorithms is necessary, which will require about 107 physical qubits. At the current level of technology, the brute-force approach to the scaling of superconducting qubit systems to such high qubit numbers is not straightforward. There is a limit to expanding the current qubit surface-mount technology, and next-generation mounting technologies such as distributed quantum computation are expected.
Recently, there has been significant interest in the idea of hardware-efficient quantum computing architectures, which use quantum systems with intrinsic protection against quantum errors. One of the promising approaches is bosonic quantum computing, which is based on the encoding of qubit states 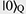 and and 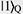 into complex superposition states of a three-dimensional (3D) superconducting cavity. In the quantum regime, a 3D microwave cavity can be considered a harmonic oscillator with an infinite number of equidistant energy levels. Each level corresponds to a quantum state with a fixed number of microwave photons in the cavity (i.e., states into complex superposition states of a three-dimensional (3D) superconducting cavity. In the quantum regime, a 3D microwave cavity can be considered a harmonic oscillator with an infinite number of equidistant energy levels. Each level corresponds to a quantum state with a fixed number of microwave photons in the cavity (i.e., states 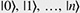 correspond to one, two, …, n photons in the cavity). The pure cavity states are equidistant and cannot be used for qubit encoding because it is difficult to address only two of them without exciting other states. In bosonic computing, this issue is solved by encoding qubit states correspond to one, two, …, n photons in the cavity). The pure cavity states are equidistant and cannot be used for qubit encoding because it is difficult to address only two of them without exciting other states. In bosonic computing, this issue is solved by encoding qubit states 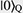 and and 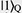 into superposition cavity states, such as into superposition cavity states, such as 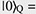 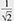  and and  , by using an additional “ancilla” superconducting qubit coupled to the cavity. The advantage of bosonic quantum computing is that the main error mechanism is the cavity-photon loss, which is relatively easy to detect and correct. , by using an additional “ancilla” superconducting qubit coupled to the cavity. The advantage of bosonic quantum computing is that the main error mechanism is the cavity-photon loss, which is relatively easy to detect and correct.
In this article, a new type of tunable qubit, 3D hybrid flux qubit, is described that can be used for bosonic computing. Due to their tunability, such qubits can be used as ancillas for achieving dynamical coupling between photonic states of different cavities, which will be an important step towards building a large-scale bosonic quantum computer.
2. Qubit design and experimental results
Our 3D hybrid qubit consists of a capacitively shunted (c-shunt) 2D flux qubit embedded in a 3D copper cavity, as shown in Figs. 1 and 2 [5]. C-shunt flux qubits were proposed theoretically in 2007 [6] and were initially fabricated in a 2D architecture [7]. The novelty of our 3D hybrid qubit design relies on the combination of a 2D c-shunt flux qubit with a 3D microwave resonator.
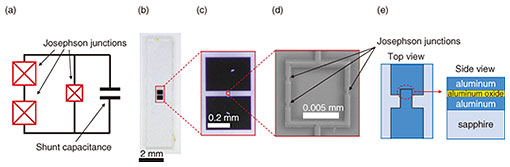
Fig. 1. (a) A schematic of a 2D superconducting flux qubit with a shunt capacitance. (b, c, d) Images of this qubit. (e) A schematic of a Josephson junction.
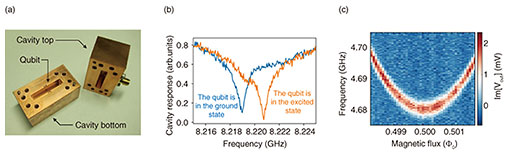
Fig. 2. (a) A photo of the 2D c-shunt flux qubit mounted inside a 3D microwave cavity. (b) Qubit state can be determined from the cavity resonance frequency. (c) The qubit frequency can be tuned by applying a magnetic flux through the qubit loop (¦µ0 is the magnetic flux quantum, ¦µ0 ≈ 2 ¡ß 10¡Ý15 Wb).
A schematic and images of the 2D c-shunt flux qubit used as a part of our 3D hybrid qubit are shown in Figs. 1(a)–(d). The 2D qubit consists of an aluminum superconducting loop interrupted by three Josephson junctions (Figs. 1(a), (d)). Two junctions are identical, while the third junction is smaller than the other two. The small junction is shunted by a large coplanar capacitor consisting of two large rectangular aluminum pads (Figs. 1(a)–(c)). The 2D qubit is fabricated on a sapphire substrate, and Josephson junctions are fabricated using double-angle shadow evaporation of aluminum. Each Josephson junction consists of two superconducting aluminum layers separated by a thin (about 2 nm) insulating layer of aluminum oxide formed by oxidizing the aluminum film in oxygen atmosphere (Fig. 1(e)).
The substrate with the 2D c-shunt flux qubit is embedded in a 3D microwave cavity (Fig. 2(a)), and the device is cooled to 10 mK (approximately –273°C) using a dilution refrigerator. Because of the capacitive coupling between the qubit and cavity, the cavity-resonance frequency shifts to higher frequencies when the qubit is excited from the ground state to the excited state (Fig. 2(b)); hence, the state of the qubit can be determined from the cavity-resonance frequency. The qubit-transition frequency can be tuned by applying an external magnetic flux Φe = B × S, where B is the applied magnetic field and S is the qubit loop area (Fig. 2(c)).
This 3D hybrid flux qubit demonstrates long T1 in the range 60–90 µs [5] and T2 up to 100 µs [8] (Fig. 3(a)). These coherence times exceed those reported for other types of flux qubits (Fig. 3(b)) and are comparable to relaxation times observed in fixed-frequency qubits such as transmon qubits.
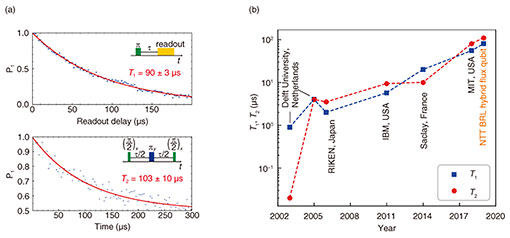
Fig. 3. (a) Results of energy-relaxation and dephasing measurements of our 3D hybrid flux qubit. (b) Evolution of relaxation times in superconducting flux qubits.
3. Outlook
Our 3D hybrid flux qubit demonstrates relaxation times comparable to those reported for transmon qubits, which are typically used in superconducting platforms. This makes 3D hybrid flux qubits a possible alternative to transmons for applications in quantum computing. Due to its intrinsic 3D structure, this new design can be particularly useful for bosonic computing.
Quantum computing using bosonic states of 3D superconducting cavities is a promising approach for hardware-efficient quantum-information processing. The possibility of the error-correction of a single qubit encoded in cavity photon states has been recently demonstrated [9]. Next important steps will be improving the error-correction protocol to achieve full fault-tolerant protection and demonstrating logical operations (gates) between multiple error-corrected qubits. Two-qubit gates can be achieved by coupling qubits encoded in two cavities via ancilla superconducting qubits. For example, a controlled NOT (CNOT) gate between two cavity qubits using a fixed-frequency transmon qubit has been reported [10]. However, one of the problems of the transmon-based scheme is that the coupling between the cavities is fixed; therefore, there is an unwanted interaction between qubits encoded in cavity states even in the idle state. This issue can be solved using dynamical coupling schemes, in which the interaction between the cavities is switched on only for a short time. Our 3D hybrid flux qubit is uniquely suited for this purpose since its frequency can be adjusted by applying an external magnetic field. A possible concept of the dynamic coupling protocol using our 3D hybrid flux qubit is shown in Fig. 4. The coupling between cavity qubits is facilitated by two ancilla qubits capacitively coupled to each other (Fig. 4(a)). Ancillas are coupled to different cavities, and the interaction between the cavities can be switched on and off using the so-called iSwap gate [11] between ancilla qubits (Fig. 4(b)).
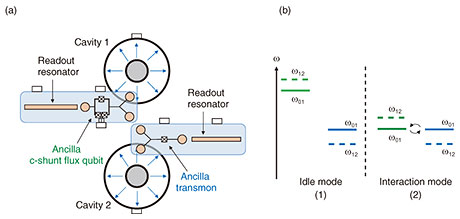
Fig. 4. (a) Schematic of a device to achieve two-qubit logical operation (gate) between logical qubits encoded in bosonic states of two coaxial 3D cavities. The dynamic coupling between bosonic qubits is based on the iSwap gate between ancilla qubits. (b) Schematic representation of the iSwap gate between ancilla qubits. (1) Ancilla qubits are in idle state separated by large detuning. (2) Ancilla qubits are tuned into resonance with each other.
In conclusion, the new type of 3D superconducting qubit described in this article combines long coherence times with frequency tunability. Future work will explore possible applications of such high-coherence tunable qubits in hardware-efficient schemes of quantum computing, such as bosonic computing.
References
| [1] |
F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. S. L. Brandao, D. A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, J. R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Yuezhen Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven, and J. M. Martinis, “Quantum Supremacy Using a Programmable Superconducting Processor,” Nature, Vol. 574, pp. 505–510, 2019. |
| [2] |
E. J. Zhang, S. Srinivasan, N. Sundaresan, D. F. Bogorin, Y. Martin, J. B. Hertzberg, J. Timmerwilke, E. J. Pritchett, J. B. Yau, C. Wang, W. Landers, E. P. Lewandowski, A. Narasgond, S. Rosenblatt, G. A. Keefe, I. Lauer, M. B. Rothwell, D. T. McClure, O. E. Dial, J. S. Orcutt, M. Brink, and J. M. Chow, “High-fidelity Superconducting Quantum Processors via Laser-annealing of Transmon Qubits,” arXiv:2012.08475, 2020. |
| [3] |
M. A. Rol, F. Battistel, F. K. Malinowski, C. C. Bultink, B. M. Tarasinski, R. Vollmer, N. Haider, N. Muthusubramanian, A. Bruno, B. M. Terhal, and L. DiCarlo, “Fast, High-fidelity Conditional-phase Gate Exploiting Leakage Interference in Weakly Anharmonic Superconducting Qubits,” Phys. Rev. Lett., Vol. 123, No. 12, 120502, 2019. |
| [4] |
N. Ofek, A. Petrenko, R. Heeres, P. Reinhold, Z. Leghtas, B. Vlastakis, Y. Liu, L. Frunzio, S. M. Girvin, L. Jiang, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf, “Extending the Lifetime of a Quantum Bit with Error Correction in Superconducting Circuits,” Nature, Vol. 536, pp. 441–445, 2016. |
| [5] |
L. V. Abdurakhimov, I. Mahboob, H. Toida, K. Kakuyanagi, and S. Saito, “A Long-lived Capacitively Shunted Flux Qubit Embedded in a 3D Cavity,” Appl. Phys. Lett., Vol. 115, No. 26, 262601, 2019. |
| [6] |
J. Q. You, X. Hu, S. Ashhab, and F. Nori, “Low-decoherence Flux Qubit,” Phys. Rev. B, Vol. 75, No. 14, 140515(R), 2007. |
| [7] |
F. Yan, S. Gustavsson, A. Kamal, J. Birenbaum, A. P. Sears, D. Hover, T. J. Gudmundsen, D. Rosenberg, G. Samach, S. Weber, J. L. Yoder, T. P. Orlando, J. Clarke, A. J. Kerman, and W. D. Oliver, “The Flux Qubit Revisited to Enhance Coherence and Reproducibility,” Nat. Commun., Vol. 7, 12964, 2016. |
| [8] |
L. V. Abdurakhimov, I. Mahboob, H. Toida, K. Kakuyanagi, Y. Matsuzaki, and S. Saito, “Driven-state Relaxation of a Coupled Qubit-defect System in Spin-locking Measurements,” Phys. Rev. B, Vol. 102, No. 10, 100502(R), 2020. |
| [9] |
N. Ofek, A. Petrenko, R. Heeres, P. Reinhold, Z. Leghtas, B. Vlastakis, Y. Liu, L. Frunzio, S. M. Girvin, L. Jiang, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf, “Extending the Lifetime of a Quantum Bit with Error Correction in Superconducting Circuits,” Nature, Vol. 536, 441, 2016. |
| [10] |
S. Rosenblum, Y. Y. Gao, P. Reinhold, C. Wang, C. J. Axline, L. Frunzio, S. M. Girvin, L. Jiang, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf, “A CNOT Gate between Multiphoton Qubits Encoded in Two Cavities,” Nat. Commun., Vol. 9, 652, 2018. |
| [11] |
R. Barends, C. M. Quintana, A. G. Petukhov, Y. Chen, D. Kafri, K. Kechedzhi, R. Collins, O. Naaman, S. Boixo, F. Arute, K. Arya, D. Buell, B. Burkett, Z. Chen, B. Chiaro, A. Dunsworth, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, T. Huang, E. Jeffrey, J. Kelly, P. V. Klimov, F. Kostritsa, D. Landhuis, E. Lucero, M. McEwen, A. Megrant, X. Mi, J. Mutus, M. Neeley, C. Neill, E. Ostby, P. Roushan, D. Sank, K. J. Satzinger, A. Vainsencher, T. White, J. Yao, P. Yeh, A. Zalcman, H. Neven, V. N. Smelyanskiy, and J. M. Martinis, “Diabatic Gates for Frequency-tunable Superconducting Qubits,” Phys. Rev. Lett., Vol. 123, No. 21, 210501, 2019. |
 |
- Leonid V. Abdurakhimov
- Research Specialist, Superconducting Quantum Circuits Research Group, NTT Basic Research Laboratories.
He received a B.Sc. and M.Sc in applied physics and mathematics from Moscow Institute of Physics and Technology, Russia, and a Ph.D. in physics from the Institute of Solid State Physics, Russia, in 2005, 2007, and 2010. He was a research scientist at the Institute of Solid State Physics, Russia, from 2011 to 2012 then held postdoctoral positions at Okinawa Institute of Science and Technology, Japan (2013–2015), Cambridge University, UK (2016), and University College London, UK (2017–2018). He joined NTT Basic Research Laboratories in 2019 as a research specialist. His current research interests are superconducting quantum circuits and spin-based hybrid quantum systems. He is a member of the American Physical Society (APS).
|
 |
- Imran Mahboob
- Distinguished Researcher, Superconducting Quantum Circuits Research Group, NTT Basic Research Laboratories.
He received an MPhys. in theoretical physics from the University of Sheffield, UK, in 2001 and a Ph.D. in physics from the University of Warwick, UK, in 2004. He joined NTT Basic Research Laboratories in 2005 and had been researching electromechanical systems to harness their nonlinear dynamics to develop phonon-based information technologies. Since 2017, he has been engaged in the development of microwave quantum optics for quantum technology applications. He was appointed as Distinguished Scientist of NTT in 2013. He is a member of the Institute of Physics (IoP) and APS.
|
 |
- Hiraku Toida
- Research Scientist, Superconducting Quantum Circuits Research Group, NTT Basic Research Laboratories.
He received a B.E., M.E., and Ph.D. in arts and sciences from the University of Tokyo in 2008, 2010, and 2013. He joined NTT Basic Research Laboratories in 2013, where he studied coherent coupling between an erbium-doped crystal and a superconducting flux qubit. From April to June of 2014, he was with NTT Microsystem Integration Laboratories, where he studied numerical simulation of plasmonic waveguides. He is currently studying highly sensitive spin sensing using superconducting quantum circuits. He is a member of the Physical Society of Japan (JPS) and the Japan Society of Applied Physics (JSAP).
|
 |
- Kosuke Kakuyanagi
- Senior Research Scientist, Superconducting Quantum Circuits Research Group, NTT Basic Research Laboratories.
He received a B.S., M.S., and Ph.D. in science from Hokkaido University in 2000, 2002, and 2005. He joined NTT Basic Research Laboratories in 2005 and has been studying superconducting qubits. He is currently engaged in an experimental study of physics on superconducting quantum circuits. He is a member of JPS and JSAP.
|
 |
- Shiro Saito
- Senior Distinguished Researcher and Group Leader of Superconducting Quantum Circuits Research Group, NTT Basic Research Laboratories.
He received a B.E., M.E., and Dr.Eng. in applied physics from the University of Tokyo in 1995, 1997, and 2000. He joined NTT Basic Research Laboratories in 2000. Since then he has been engaged in quantum information processing using superconducting circuits. He was a guest researcher at Delft University of Technology from 2005 to 2006. He was a guest associate professor at Tokyo University of Science from 2012 to 2020 and currently a guest professor. He was appointed as Distinguished Scientist of NTT in 2012 and Senior Distinguished Researcher in 2021. He is a member of JPS and JSAP.
|
↑ TOP
|



















