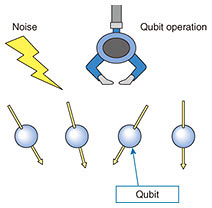
Theoretical Approach to Overcome Difficulties in Implementing Quantum Computers

1. Quantum computers with limited resources and/or restricted functions

Expectations for the outstanding potential of quantum computers have surged recently; therefore, national projects, startups, and major companies are competing fiercely in developing quantum computers. In the near future, however, we can expect only restricted quantum computers in terms of the amount of computational resources and variety of available functions rather than full-fledged quantum computers. This is because large-scale fault-tolerant quantum computers require implementation technologies that meet extremely strict conditions. To develop such technologies as soon as possible, various studies on basic research are currently being conducted worldwide.

A relevant theoretical approach is to clarify with theoretical knowledge the limitation of the computational power of quantum computers with limited resources and/or restricted functions due to difficulties in physical implementation. In this article, we introduce several theoretical research studies for deriving the maximum power of such restricted quantum computers.

2. Overcoming difficulty in reducing noise

Current assumed quantum computers prepare and initialize a set of qubits then successively execute operations on one or two qubits. After measuring the resulting state, we obtain the output bit-sequence (Fig. 1). By designing these operations on the qubits depending on the problem, it is possible to make the output provide information that solves the particular problem. For this purpose, the qubits must be unaffected by noise. A standard method for achieving this is using quantum error-correcting codes for large-scale quantum computers. This method involves encoding information on a single logical qubit with multiple physical qubits in a redundant manner, which can protect quantum information from noise. To use such a method, the noise level for physical qubits must be below a certain level. However, this requirement has not yet been met.

Fig. 1. The current model of quantum computers.

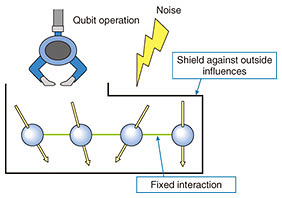
The fact that we can manipulate some qubits directly means that those qubits will be affected by the environment (e.g., noise). In other words, an abundance of controllability means that there is also a path along which noise may enter. Therefore, if an object that can handle quantum information has limited degrees of freedom to manipulate directly, the effect of noise will be small. However, quantum computers originate from ordinary computers; thus, we assume we can apply many types of operations directly for qubits in quantum computers. As a result, practical quantum information processing under restricted controllability has not been considered.

We theoretically investigated a situation in which only restricted operations can be applied [1], which would be useful when we limit controllability to reduce noise. This situation is as follows (indirect quantum control (Fig. 2)). We prepare two quantum systems. One is an internal system, which is directly incontrollable, and the other is an external system, which can be directly manipulated at will. Quantum information is transferred back and forth between the two systems through a fixed interaction. We found that the internal system can be divided into two parts. The first part affects the external system and the second part does not. Moreover, if the dimension of the external system is more than 3, the first part can be indirectly manipulated at will. In other words, any indirectly controlled quantum system has sufficient ability as a quantum information processor when the dimension of the directly controllable system (i.e., external system) is more than 3. However, this investigation only focused on the possibility or impossibility of achieving indirect quantum control and did not provide an answer to more in-depth questions such as how long it takes to implement the desired indirect quantum control. Since indirect quantum control has never been systematically analyzed, our investigation serves as a theoretical foundation for indirect quantum control, and further investigation is needed to answer more practical questions. In this sense, we have shown that indirect quantum control has the potential for denoising, but the specific process of denoising must be discovered through future investigations.

Fig. 2. The model of quantum information processor by indirect quantum control.

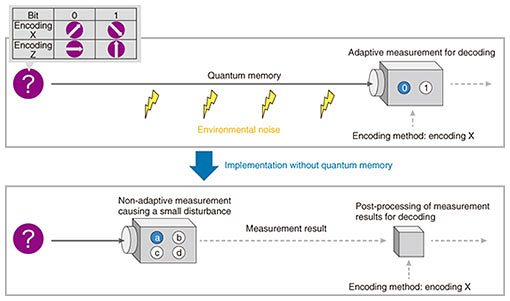
3. Overcoming difficulty in achieving quantum memory

A quantum computer sequentially repeats two procedures: measuring a highly controlled quantum system^*1 in an appropriate order and controlling the system on the basis of the previous computation results. Since quantum measurements inevitably disrupt the quantum system even if they are carried out accurately, the order of measurements is strictly restricted depending on the algorithm. Thus, the ability of changing the order of quantum measurements enables the design of many quantum algorithms. It also improves the key rate of the quantum key distribution, a highly secure cryptography.

A long (waiting) time until measurements are carried out, however, requires quantum memory, a mechanism to protect a quantum system from environmental noise. Although many methods of implementing quantum memory have been proposed, the number of measurements that can be executed within the memory time is much less than that required for a large-scale quantum computer.

We can carry out certain types of measurements that depend on previous computation results, i.e., adaptive measurements, before knowing the previous computation results and without disturbing future computation results, which makes quantum memory unnecessary. However, there is no known example of quantum-information-processing tasks benefitting from such adaptive measurements.

In our previous study [2], we found an application of adaptive measurements not requiring quantum memory in state discrimination, which is used as a subroutine in many quantum-information-processing tasks. Consider decoding one bit by measuring a quantum state that encodes the bit by using an encoding method randomly chosen from a pair of encoding methods. Intuitively, we may fail to decode a bit perfectly unless we carry out adaptive measurement depending on the encoding method. However, it is possible to decode the bit perfectly by using only non-adaptive measurement and simple post processing for certain pairs of encoding methods, as shown in Fig. 3. Since not all pairs of encoding methods enable perfect decoding, we derive succinct criteria for a pair of encoding methods to be perfectly decodable. Such perfectly decodable pairs can be used as a quantum-key distribution protocol with a higher key rate than a widely used encoding method if we can ignore communication-channel noise. However, since channel noise is not negligible in practical communication between distant parties, we need to conduct a detailed analysis of the key rate in practical channel noise.

Fig. 3. Decoding one bit without using quantum memory.

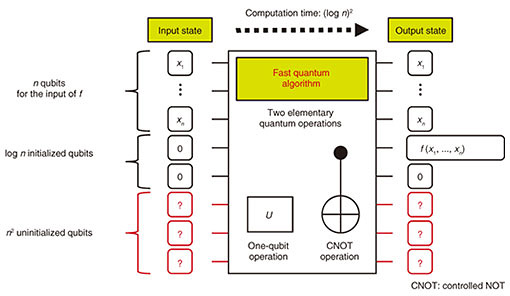
4. Overcoming difficulty in initializing qubits

Fast quantum algorithms are required to achieve high-speed computation on quantum computers. Such algorithms are usually designed under the assumption that many qubits initialized to state 0 are available. These initialized qubits are useful for storing various intermediate results during a computation, which, for example, allows us to design highly parallel algorithms. Therefore, the availability of many initialized qubits significantly contributes to designing fast quantum algorithms.

Although initializing many qubits plays a key role in designing fast quantum algorithms, preparing such qubits is beyond the reach of current implementation technology. In fact, there is a limit on initialization accuracy; thus, when many qubits are initialized using current technology, some of the qubits can sometimes be in unintended states. Limiting the number of qubits to be initialized increases feasibility. However, with only a small number of initialized qubits, it is difficult to design fast quantum algorithms.

We therefore focus on uninitialized qubits as computational resources for designing fast quantum algorithms together with a small number of initialized qubits. The states of uninitialized qubits are unknown, but, as with common qubits, their states can be changed by applying quantum operations. Since uninitialized qubits do not require initialization by definition, they are relatively easy to prepare.

Under the assumption that many uninitialized qubits and a small number of initialized qubits are available (Fig. 4), we designed fast quantum algorithms for computing symmetric Boolean functions (e.g., the logical OR function), which are key ingredients of more complicated quantum algorithms [3]. However, it seems difficult to design fast quantum algorithms for the same functions with only a small number of initialized qubits. Therefore, our algorithms indicate that the use of uninitialized qubits significantly contributes to designing fast quantum algorithms.

Fig. 4. Computing function f: {0,1}ⁿ → {0,1} with many uninitialized qubits and a small number of initialized qubits.

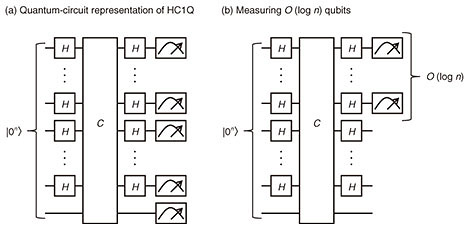
5. Overcoming restrictions on architectures

Several quantum computing models with functionality restricted to improve their feasibility have recently been proposed. In this section, by using the Fourier hierarchy, a hierarchy of quantum circuits, we introduce our previously proposed quantum computing model Hadamard-classical circuit with one-qubit (HC1Q) [4], as shown in Fig. 5(a). In HC1Q, the basis transformations with Hadamard gates H^*2 are executed before and after the coherent classical computation. Note that no basis transformations are executed for the lowest qubit. As the level of the Fourier hierarchy becomes higher, the computational capability of quantum circuits also becomes higher. In particular, all quantum circuits contained in the first level can be efficiently simulated with classical computers. Therefore, to demonstrate the superiority of quantum computing over classical counterparts (i.e., quantum computational supremacy), we have to use quantum circuits in the second or higher level. Since HC1Q has quantum computational supremacy even though it is in the second level of the Fourier hierarchy, it can be considered as one of the most restricted quantum computing models with advantage over classical computers. More formally, we have shown that if HC1Q can be efficiently simulated with a classical computer, then the polynomial hierarchy, a concept in computational complexity theory^*3, collapses to its second level. Polynomial hierarchy is a hierarchy of decision problems that can be answered with YES or NO and is strongly believed to not collapse. By associating two completely different hierarchies, i.e., the Fourier and polynomial hierarchies, we have shown the quantum computational supremacy of HC1Q. As shown in Fig. 5(a), all input qubits are measured in HC1Q. What happens if only a small number of qubits are measured? Interestingly (see Fig. 5(b)), the computational capability becomes equivalent to or strictly less than that of classical computers.

Fig. 5. Quantum computing model in the second level of the Fourier hierarchy. (a) Quantum-circuit representation of HC1Q. (b) Modified version, where the number of measured qubits is decreased.

6. Outlook

Research on both software (i.e., algorithms) and hardware for quantum computers is essential for high-speed quantum computing. With our theoretical expertise, we will explore designing algorithms that solve important problems very fast on quantum computers as well as develop theoretical methods, such as those discussed in this article, to maximally extract computational power from quantum computer hardware.

References

[1]	G. Kato, M. Owari, and K. Maruyama, “Algebra and Hilbert Space Structures Induced by Quantum Probes,” Ann. Phys., Vol. 412, 168046, 2020.
[2]	S. Akibue and G. Kato, “Perfect Discrimination of Nonorthogonal Quantum States with Posterior Classical Partial Information,” Phys. Rev. A, Vol. 99, No. 2, 020102, 2019.
[3]	Y. Takahashi and S. Tani, “Power of Uninitialized Qubits in Shallow Quantum Circuits,” Theor. Comput. Sci., Vol. 851, pp. 129–153, Jan. 2021.
[4]	T. Morimae, Y. Takeuchi, and H. Nishimura, “Merlin-Arthur with Efficient Quantum Merlin and Quantum Supremacy for the Second Level of the Fourier Hierarchy,” Quantum, Vol. 2, 106, 2018.