|
|||||||||||||
|
|
|||||||||||||
|
Feature Articles: The Forefront of Nanomechanics Research Vol. 20, No. 4, pp. 37–42, Apr. 2022. https://doi.org/10.53829/ntr202204fa6 New Method of Chaos Generation by Using Nanomechanical OscillatorAbstractChaos is a naturally observed phenomenon characterized by its irregular and complicated behavior. Although chaos has been long recognized as a topic of academic importance, its implementation in modern technological products and devices remains wanting. However, with advances in security and artificial-intelligence technologies, attempts to use chaotic signals have begun to materialize. In this article, we report on a new simple and versatile chaos-generation method using a nanomechanical oscillator developed by NTT laboratories. Keywords: chaos, nanomechanics, libration 1. What is chaos?If you look up the word “chaos” on the Internet, you are likely to find loose definitions, such as “an expression describing a chaotic situation or aspects in which various elements are jumbled and incoherent.” Chaos conjures up images of unpredictable irregularities, such as “the stock prices are chaotic right now,” or “my desk is chaotic.” In mathematics, however, chaos is a well and rigorously defined subject of study. If one wants a definition, although not mathematically exact, one can say “chaos is a seemingly disordered complex movement that evolves according to well set laws.” For physicists and engineers, chaos has attracted attention for its behavior that lies between irregular random motion and periodic regular motion [1]. For a researcher, chaos has several attributes. First, it has reproducibility, meaning that under the same initial conditions a chaotic system will repeatedly show the same behavior. Thus once the initial state is perfectly known, it is, in principle, completely predictable. This is an important property that distinguishes it from random motion. However, chaos is characterized by the butterfly effect, in which the tiniest difference in the initial conditions will cause a large change, which practically makes chaos all but unpredictable. In principle, if the initial state is completely known, one can accurately predict the future evolution of the system; however, even the slightest mistake or difference in the initial state—say 0.001%—will make a large difference in how the system behaves after a while. Perhaps a good example would be to imagine the bouncing of a rugby ball. It would not surprise you to know that the motion of a rugby ball follows the laws of physics, the same laws that describe bowling balls and airplanes, and according to those laws, if the initial conditions can be reproduced (speed, angle, twist…), then the motion of the rugby ball can also be reproduced. However, anyone who enjoys watching a rugby match understands how difficult that is, and how only slight changes in angle or speed would quickly lead to a different trajectory and a loss for your favorite rugby team. Another characteristic of chaos is that such seemingly complex behavior can occur in mathematically simple dynamical systems. To be clear, chaos does occur in large systems with many components (degrees of freedom as the mathematicians call them). Think of, for example, the turbulent waters of a flowing river or the behavior of weather that depends on many parameters, e.g., humidity, wind speed, cloud cover, precipitation, temperature, and pressure. However, the appeal of chaos is that it equally appears in simpler systems. For instance, it has long been known that three stars orbiting each other could lead them to have chaotic orbits, even if we neglect the influence of every other object in the universe upon these three stars. That such simple systems can generate such a complex behavior is certainly a property that engineers, physicists, and mathematicians find particularly interesting. Despite this interest in chaos as a scientific phenomenon, it has remained rather untamed and difficult to apply technology. Nevertheless, serious efforts are underway to put the properties of chaos to applied use, such as secure communication, where chaos’ complex signals are used to encrypt and mask information, or the use of chaos in efficient machine learning that uses a state known as the edge of chaos*1 to execute such computation efficiently. Some of the questions of practical interest, if chaos is to serve in applications, are what are the necessary conditions to reliably generate chaos?, Can such reliable chaos be generated using low-power methods?, and What exactly are the properties of the generated chaos? Motivated by this background of challenges, we developed and demonstrated a chaos-generation method that can successfully generate chaos in a reliable fashion all while using low power in a microelectromechanical device. The following sections describe this method.
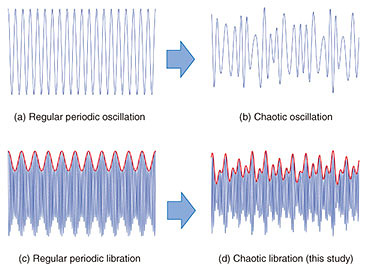
2. Chaos generation via libration motionMicroelectromechanical systems (MEMS), as their name suggests, are miniaturized devices that can either produce or detect mechanical forces. Other than their size, MEMS devices are distinct from conventional electromechanical systems (think electric motors or even sound speakers) in that they are fabricated using the same materials and processes that are used to make the electronic devices and integrated circuits that power our cellphones, computers, and cars. Therefore, MEMS devices have been extremely successful as various sensors, high-frequency filters, accelerometers, gyroscopes, and portable digital projectors. It is therefore not surprising that efforts to generate chaos using MEMS or further-miniaturized nanoelectromechanical systems (NEMS) mechanical oscillators*2 have attracted significant attention. Such efforts are motivated by the availability of low-cost MEMS/NEMS devices on the one hand, and on the other the possibility to directly integrate them with electronics in packages that combine both sensors, signal processors, and machine learning. Despite multiple successful demonstrations of chaos generation using MEMS oscillators, they remained more in the realm of fundamental research rather than application. One of the main reasons is the need for complex device geometries such as comb-shaped electrodes. Another especially impactful reason is the need to apply high voltages on the order of several tens of volts, which may not seem very large by comparison to the electric wall plug but considered quite substantial by microelectronics standard. Researchers working at NTT laboratories have demonstrated a simple and low-power, i.e., low voltage, method for the generation of chaos in MEMS/NEMS devices by simply applying two slightly different frequencies to the mechanical device. This method leverages a type of motion known as libration*3 to induce chaos with drive voltages on the order of a fraction of a volt [2]. Figure 1 shows the difference in the transition to chaos generated using a MEMS/NEMS oscillator between the classical method and above method developed by NTT laboratories. First, consider the classical method, with which the oscillatory is forced from a regular periodic motion (Fig. 1(a)) into producing a chaotic motion (Fig. 1(b)). To achieve such a transition, it is necessary to have a large structure, known as a comb-shaped electrode, and apply a high voltage to find the right conditions to transform the periodic motion into chaotic oscillations.
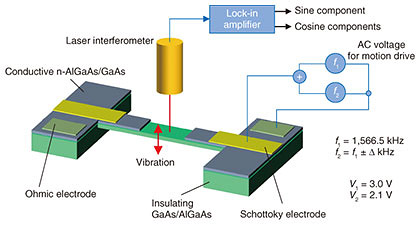
With the new method, chaos generation is facilitated by the use of libration motion, where the periodic motion is composed of two frequencies not just one (Fig. 1(c)), and the first periodic motion is modified periodically by the second periodic motion. This is not unlike amplitude modulation (AM) found in AM radio. The team of NTT researchers realized that it is possible to leverage this motion in a nonlinear nanomechanical oscillator to create a chaotic motion without the high voltage and special design constraints found with the classical method (Fig. 1(d)). The researchers were equally able to successfully identify the necessary conditions for the generation of chaotic motion. Figure 2 shows a diagram of the experimental equipment used in this study. The beam structure is made from layers of piezoelectric semiconducting materials known as gallium arsenide (GaAs) and aluminum gallium arsenide (AlGaAs). By applying an alternating current (AC) voltage to the electrodes shown in the figure, the beam starts to oscillate in the direction shown with the red arrow. The vibration of the beam is measured using a laser interferometer device, and the amplitude of vibration is split into a sine and cosine components using a lock-in amplifier (note that these are the same sine and cosine components that telecommunication engineers are so familiar with).
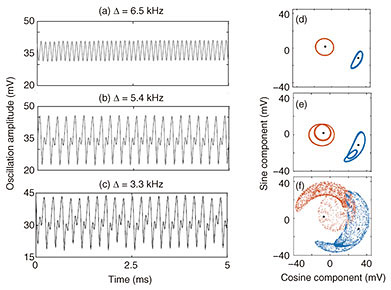
The method for generating the libration motion and chaos is quite simple. Apply two different AC frequencies (f1 and f2 in the figure) to drive the mechanical device, if the frequencies are not very different, then they will cause a beat that is equal to their difference. This beat is what causes the AM shown in Fig. 1(c). Another way to visualize this AM is to draw the sine and cosine components, as done in Fig. 3 (right column; (d), (e), (f)). By applying the two AC frequencies, the AM envelope, shown in Fig. 3 (left column; (a), (b), (c)), is periodic at first (Fig. 3(a)). This periodicity is seen as a simple closed orbit (also called libration orbit, hence libration motion) if observed in the sine and cosine plots (Fig. 3(d)). By slightly changing the drive voltages, the AM envelope undergoes what is called a period-doubling bifurcation, and we see clearly that there is a new second period even though we have not changed the frequencies of the two drive tones (Figs. 3(b) and (e)). This period-doubling bifurcation is a sign that we are well on our way to chaos, and by changing the drive forcing just a little bit more, the AM envelope and libration motion both demonstrate a breakdown of the main periodic motion and onset of a chaotic motion (Figs. 3(c) and (f)).
To rigorously demonstrate that we have achieved a chaotic motion, we need to calculate the Lyapunov exponent*4 which quantitatively confirms the property of chaos to produce large changes due to small differences in initial conditions. In our collaboration with Tokyo Institute of Technology, we confirmed that such a property is indeed present using numerical calculations and simulations. This new chaos-generation method has three major advantages. First, it is possible to use small voltages (~1 V in the experiment), which makes it easy to interface with current low-power electronic circuits. Second, because large structures (by MEMS standards), such as comb-shaped electrodes, are not required, the process of miniaturization and integration is more convenient. The third advantage is that this method is not limited to mechanical oscillators but can be implemented in a variety of devices including optical resonators used in laser technology, therefore combining the roles of optical communications and secure encryption in a single system.
3. Future outlookIn this article, we presented a new chaos-generation method using libration motion in a nanomechanical oscillator was presented. This method can generate chaos in nanomechanical devices with a drive voltage that is more than an order of magnitude smaller than with the classical method, all while being more suitable for miniaturization and integration. The tradeoff being, that since, as shown in Fig. 1, the frequency of the generated chaos is smaller than that of the original vibrations, a higher frequency oscillator is needed to generate a chaotic signal with a practical bandwidth. We succeeded in demonstrating nanomechanical oscillators with frequencies up to the GHz using phononic crystals. We will continue to work on improving the performance of such systems and hope to enable applications such as machine learning using integrated nanomechanical devices. References
|
|||||||||||||