|
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
Feature Articles: The Forefront of Nanomechanics Research Vol. 20, No. 4, pp. 43–48, Apr. 2022. https://doi.org/10.53829/ntr202204fa7 Control of Elastic Waves Using Phonon Waveguides and Phononic CrystalsAbstractSounds and heat are elementary excitations of lattice vibrations called phonons. In contrast to the widespread use of electrons and photons in signal processing devices and communications systems, the use of phonons as information carriers has been extremely limited because a technique to control them has not been developed. This article describes our research on a new platform called electromechanical phononic crystal for improving the on-chip control of phonons. Keywords: phonon, phononic crystal, MEMS 1. Potential of phonons as information carriersPhonons are the elementary excitations of atoms and lattice vibrations. Sound waves with a frequency ranging from 104 to 1011 Hz are called ultrasonic waves and have long been used as a signal source for echo sounding and sonar [1]. In information-processing systems, phonons, including ultrasonic waves, are byproducts generated during device operation and have been regarded as obstacles that disturb normal operation. Therefore, they have thus far not been used as information carriers. Photons (light), which are attracting attention as the next-generation of information carriers, were originally used only in observations with instruments such as microscopes and telescopes. Later, the advent of new platforms, such as planar lightwave circuits and photonic crystals, improved the photon-control technology on the chip scale, thus led to the discovery of their present industrial value. Phonons also have a wave with dynamics compatible with photons. However, the wavelength of phonons is five orders of magnitude shorter than that of photons at a given frequency, and there is no radiation to free space and less energy loss. These physical properties are useful for satisfying the demand for further device miniaturization and energy-saving in high-frequency information-processing systems for the future Internet of Things society [1]. With that motivation, we are working to develop a platform enabling a variety of on-chip phononic operations. 2. Phononic crystals and microelectromechanical systemsPhononic crystals and microelectromechanical systems (MEMS) have long been known as phononic platforms. The former are artificial acoustic structures consisting of periodic structures of different elastic media and are the phononic analogue of photonic crystals (Fig. 1(a)) [1]. When a lattice constant (a) has a scale of the phonon wavelength (λ), the phonon-dispersion relation*1 is modulated by the periodic potential produced by the elastic structure. For example, a band gap*2 emerges in frequencies that satisfy the Bragg condition (nλ = 2a, n is a natural number), in which the phonon propagation with λ is prohibited. Furthermore, the formation of the band gap changes the dispersion curve, and the group velocity, which is determined by that slope, is also modified. Namely, phononic crystals enable us to spatially control the phonon propagation through their periodic structures. Therefore, in the field of acoustic engineering, artificial acoustic structures have been used as the basic structure for acoustic-wave control such as sound insulation. MEMS have been intensively studied, mainly in the field of electronics for semiconductor engineering. They consist of a three-dimensional mechanical structure with nanometer and micrometer scales, such as a cantilever and beam, and can sustain ultrasonic vibration electrically excited on-chip (Fig. 1(b)) [2]. The acoustic impedance difference between the beam and support substrate suppresses the dissipation of elastic vibrations to the substrate, thereby sustaining resonant vibrations with a long duration (high quality factor,
Note that the functions of these two platforms have a complementary relationship. We focused on this point and proposed a phononic platform called electromechanical phononic crystal created by the fusion of these different structures [3, 4]. This alternative system enables on-chip excitation, spatial transmission, and dynamic control of phonons simultaneously.
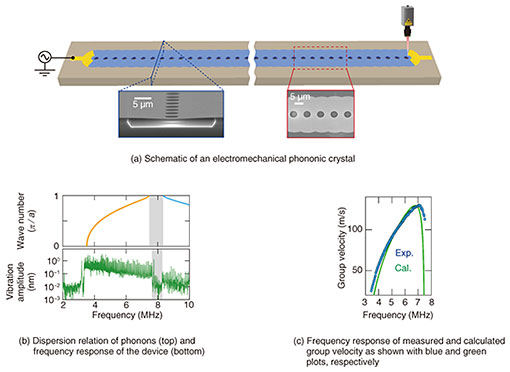
3. Electromechanical phononic crystalElectromechanical phononic crystal is composed of a waveguide structure in which 100 circular membranes with a diameter of 22 μm, made of gallium arsenide (GaAs), are periodically connected at the period of a = 8 μm, as shown in Fig. 2(a) [4]. The membranes are suspended from a GaAs substrate and vibrate like a drum. Since GaAs has piezoelectricity*6, the membrane vibration (ultrasound phonons) can be induced by applying an alternating current (AC) voltage to electrodes placed on the membrane. This elastic vibration propagates along the waveguide and affected by the elastic potential created by the periodic holes, which modulates the dispersion relation. Figure 2(b) shows the dispersion relation obtained from numerical calculations (top) and the frequency response of the phonon transmission measured in the device (bottom). In the dispersion relation, the first phononic band (orange) is formed from 3.5 to 7.4 MHz, which guides phonon vibrations in the waveguide. As a result, it is confirmed that the vibrations excited from one end of the waveguide are observed at the other end. The band reaches the Brillouin zone edge at 7.4 MHz (k = π/a, k is wave number), and the gap shown in gray appears before the next band (light blue) emerges. This is the band gap. The half λ exactly matches a (λ/2 = a), so the phonon vibrations exhibit Bragg reflections*7 at the hole locations. The phonon propagation is significantly suppressed at the bandgap spectral position. Moreover, the generation of the band gap allows a gradual decrease in the phonon-propagation speed (group velocity) because the slope of the dispersion curve becomes gentle. The measured group velocity as a function of frequency is shown in Fig. 2(c), which reveals that the propagation speed increases with frequency up to 7.0 MHz but then decreases beyond that frequency. Thus, we succeeded in experimentally observing the band gap and modulation in the group velocity, providing proof of a phononic crystal in our device.
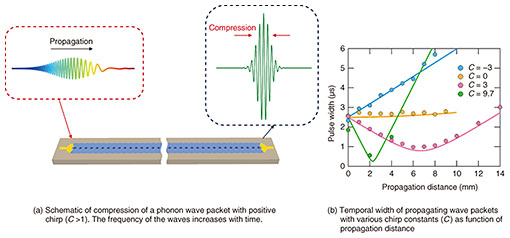
4. Phonon-wave-packet engineeringThe enriched properties of a phononic crystal enables us to control the phonon wave packets. Our device hosts group-velocity dispersion, in which the propagation speed varies with frequency. The envelope of a wave packet (pulse) has a finite temporal width and contains various frequency components near a phonon carrier frequency. Therefore, the waves in the packet travel with different speeds due to the group-velocity dispersion, resulting in expansion of the envelope. Although such waveform broadening and distortion are undesirable effects for stable wave-guiding, we used them to demonstrate wave-packet control for pulse broadening and compression in this device. A phonon wave packet with negative frequency modulation (negative chirp, C < 0) is injected from one end of the waveguide. The sign of the chirp constant (C) determines whether the frequency increases or decreases with time. If the carrier frequency is set to 5.8 MHz, the phonon with higher frequency propagates faster than the one with lower frequency in the waveguide (see Fig. 2(c)). In a negative chirp, the waves with higher frequency are located in the leading parts of the wave packet, and those with lower frequency are in the tailing parts of the wave packet at the input. Therefore, the high-frequency waves move forward, and the low-frequency ones are further delayed during the propagation, resulting in further expansion of the wave packet. When a positive chirp is injected as input, however, where the positions of lower and higher frequency waves are swapped, the wave packet is compressed during the propagation (Fig. 3(a)). Figure 3(b) shows the propagation-distance dependence of wave-packet width with various chirp constants (C). As described above, the pulse width monotonically increases with distance for negative chirp at C = −3, while it decreases for positive chirp at C = 3. However, the pulse changes from compressed to broadened at 7 mm then keeps broadening. This is because the initial distribution of the waves with different frequencies, caused by the input chirp, is fully eliminated at 7 mm. This compression effect is also enhanced by increasing the frequency-sweep range. When the chirp constant is increased from C = 3 to 9.7, the wave packet is strongly compressed from 2 to 0.6 μs. The observed minimum value is limited by the time constant of the bandpass filter in the measurement system. Therefore, the unique dispersion relation of a phononic crystal can be used to control the waveform of the propagating phonons. In this experiment, a chirp signal was used as an input, but it is also possible to achieve compression and expansion of the unchirped wave packet by the nonlinear effect, as described later [5].
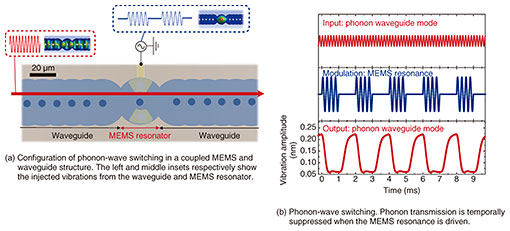
5. Switching of phonon propagationDynamic control of phonon waves can also be carried out using MEMS characteristics in electromechanical phononic crystal [3]. We installed a membrane resonator in the center of the waveguide, which is used as the external modulation node (Fig. 4(a)). This membrane can behave as a single MEMS resonating around 2 MHz because of the weak coupling with adjacent membranes. Therefore, by applying an AC voltage to an electrode placed on the surface, resonant vibrations can be excited that are spectrally and spatially isolated from the phonon waveguide modes. When the membrane is strongly excited, the stress distribution inside it is readjusted due to the large vibration amplitude. As a result, the transmission dynamics of the phonon waves passing through the center membrane is also affected by this elastic modification; thus, the transmission spectrum changes. By appropriately adjusting the frequency of the phonon waveguide mode, the transmission intensity can be reduced. Figure 4(b) shows the temporal response of the transmitted amplitude of the phonon waveguide mode measured at one end. It is excited by continuous waves at 5.745 MHz from the other end, and simultaneously the resonant vibration of the membrane at 1.855 MHz is periodically generated at an interval of 1.0 ms. The propagation amplitude decreases only when the central membrane vibrates. Thus, by using the enriched nonlinearity of the MEMS structure, the dynamic control of the phonon wave propagation is achieved in electromechanical phononic crystal.
This nonlinear MEMS technology enables a variety of phonon controls, such as vibration energy transfer, all mechanical random-access memory operation, and frequency conversion of propagating phonon waves on this chip-scale platform. 6. Ultrahigh-frequency phonons and fusion with magnonsWith electromechanical phononic crystal, we can achieve spatial and dynamic control of phonons on a chip. However, the operation frequency is as low as a few megahertz, so it is necessary to increase it up to the gigahertz band (hypersound) for practical use in, for instance, wireless communications devices. We have succeeded in fabricating a phononic crystal device operating at ultrahigh frequencies [6]. We have also explored the possibility of dynamically controlling hypersonic phonons using ferromagnetic spin waves called magnons. Combining the hypersonic structures and magnons with the electromechanical-phononic-crystal technology described in this article holds promise for the development of phononic active devices operating at ultrahigh frequencies and integrated hypersonic circuits, which will dramatically enhance the availability of phonons as information carriers. References
|
|||||||||||||||||||||||||||