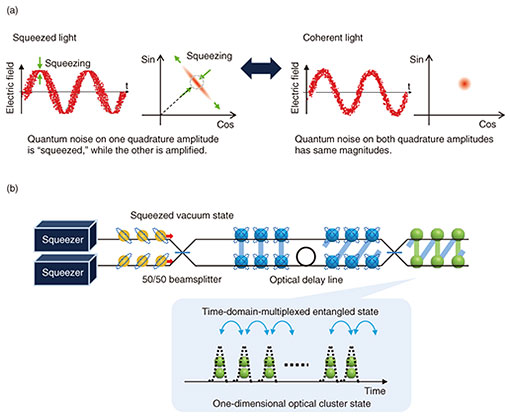
Broadband Continuous-wave Optical Quadrature Squeezer for Ultra-fast Optical Quantum Computers

1. Introduction

Research and development of universal quantum computers has accelerated worldwide, and various computing methods have been proposed using superconducting circuits, trapped ions, photons, etc. [1, 2]. We are developing an optical quantum computer that uses the amplitude and phase of propagating light as an information carrier, similar to the current optical communication technology [3]. This is because an optical quantum computer has the potential of ultra-fast clock-rate computing thanks to the high frequency of light. We are aiming to develop an overwhelmingly large-scale and high-speed universal quantum computer using time-domain multiplexing and measurement-induced quantum manipulation [4]. The most important element of this optical quantum computer is a squeezed light source. In this article, we introduce the research and development of a squeezed light source, i.e., a squeezer, which is a key device for high-speed, large-scale, universal quantum computing.

2. Squeezed state of light and its application to quantum computers

Squeezed states are non-classical states in which the quantum noise in a non-commutative quantity (momentum and position, energy and time, etc.) is compressed. Due to the uncertainty relation, the noise for the other quantities is amplified. The quadrature-amplitude-phase squeezed vacuum state of light (or simply squeezed light) has compressed quantum noise of the sinusoidal or cosine component with a wave image, as shown in Fig. 1(a). With a particle image, the squeezed light is an even-number photon state. By interfering two squeezed states with a half beamsplitter, we can deterministically generate a quantum entangled state (with 100% probability) [5]. Using multiple squeezed light sources and delay line interferometers, we are able to generate a time-domain multiplexed large-scale quantum entangled state (Fig. 1(b)) [4]. This state is called an optical cluster state and used as a resource for measurement-based quantum computation. By measuring one qubit of the optical cluster state, we can execute some quantum gates to other qubits with a methodology such as quantum teleportation [6].

Fig. 1. (a) Image of quantum noise in squeezed light. While coherent light has quantum noise equal to the sinusoidal and cosine components, squeezed light has compressed one side of the noise. The quantum noise of the other side becomes larger due to the requirement of the uncertainty principle. (b) A method for generating multiplexed large-scale quantum entangled states in the time domain using squeezed light.

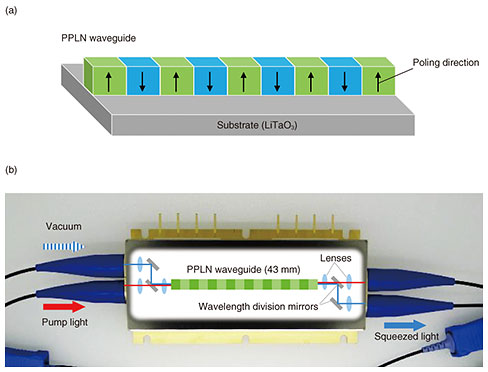
To develop a high-speed, large-scale, universal quantum computer, continuous-wave broadband high-level squeezed light is required. This is because the continuous wave and broadband nature of squeezed light maximizes time resources and enables high-speed and large-scale computational performance that cannot be achieved with other methods [7]. High-level squeezed light has quantum superposition states with even-photon-number components, which is important for quantum error correction [8].

3. PPLN-based quadrature squeezer module

Squeezed light can be generated from a nonlinear optical phenomenon. In 1985, the first generation of squeezed light was demonstrated using the third-order nonlinear optical effect of natrium vapor [9]. Since then, squeezed light has been generated in a variety of ways [10], and second- and third-order nonlinear optical effects in solids have become mainstream. Waveguide-type optical parametric amplifiers based on second-order nonlinear optical crystals are expected to exhibit broadband characteristics in principle [7]. However, nonlinear optical devices are generally difficult to fabricate, and it has been difficult to generate high-level squeezed light. To generate a high level of squeezed light, the optical waveguide must have low loss, exhibit high nonlinear optical properties, thus be resistant to strong excitation light. Low loss is required because squeezed light is easily degraded by contamination of the vacuum field associated with optical loss. We have been developing direct-bonded periodically poled lithium niobate (PPLN) waveguides, as shown in Fig. 2(a) [11]. Lithium niobate is a ferroelectric material with a wide transmission bandwidth and high second-order nonlinear optical coefficient. Thanks to its periodical poling, it is possible to enhance the nonlinear interaction of light passing through the waveguide. By bonding the waveguide directly to the substrate without using any adhesive, we fabricated devices that can operate even under pump light with watt-level intensity. Our fabrication techniques have recently enabled low-loss, high-gain optical parametric amplifiers with high pump-light tolerance.

Our group is also developing modular optical parametric amplifiers that can be easily coupled with fiber optics [12–14]. This is to enable the construction of maintenance-free optical systems in anticipation of practical applications. Quantum optics experiments had been conducted on an optical table with many mirrors and lenses arranged with high precision to verify the proof-of-principles. These optical systems require constant precise adjustment, and this has been a problem that needs to be solved for practical applications. As shown in Fig. 2(b), our module has a structure in which the pump light and squeezed light are separated inside the module, and each is efficiently coupled to an optical fiber [12–14]. This fiber-pigtailed module will greatly advance the development of practical-use optical quantum computers because we can combine various highly reliable and high-performance optical components, which are cultivated in the field of optical communications.

Fig. 2. (a) Schematic view of a PPLN waveguide. The waveguide core is directly bonded to the substrate. (b) Fiber-coupled optical parametric amplifier. Wavelength-division mirrors and lenses are installed inside so that the pump light and squeezed light are separated and injected to each output optical fiber [14].

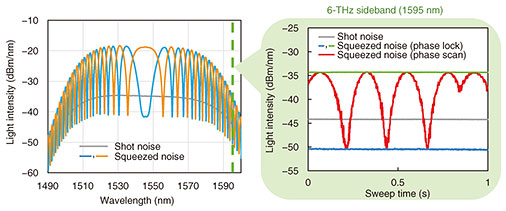
4. Squeezing-level measurement

The squeezing levels have conventionally been measured by balanced homodyne detection [15]. With this method, the squeezed light interferes with a local oscillator, the frequency of which is the same as the center frequency of the squeezed light, by using a half beamsplitter. The difference between the output intensities of the two paths is then extracted as an electrical signal by using a balanced photodetector. Accordingly, the bandwidth of the squeezed light measured using balanced homodyne detection is limited by the bandwidth of the electrical circuit up to a few gigahertz. Therefore, we developed a method for measuring quantum-noise intensity up to THz-class broadband components by further optical parametric amplification of the squeezed light [16]. This means that the quantum information is converted directly into classical light, whereas previous methods (balanced homodyne detection) convert it onto the classical state of an electrical signal. Figure 3 shows the results of noise-intensity-level measurements. The experimental results indicate that the noise of the squeezed light is suppressed by more than 6 dB compared with the shot-noise level, even for THz-order sideband components [14]. This value is more than the 4.5 dB required to generate two-dimensional optical-cluster states, which enables multi-qubit quantum computation. This is the world’s highest value for squeezing using a waveguide-type optical parametric amplifier with an all-optical-fiber-closed system.

Fig. 3. Quantum-noise-intensity measurement results for squeezed light. The noise level was more than 6 dB lower than the shot noise level. The squeezing level was maintained over the broadband component above 6 THz [14].

5. Conclusion

We reported on the generation of continuous-wave, broadband squeezed light for the development of a high-speed, large-scale, universal quantum computer. The squeezing of 6 THz and more than 6 dB was achieved using an optical parametric amplifier consisting of a PPLN waveguide, which was developed by NTT. The device can be implemented as a fiber-coupled module to enhance compatibility with optical communication components and is being fabricated in anticipation of the future development of quantum computers. We aim to achieve a higher level by improving the device-fabrication technique and optimizing the design and are attempting more than 10-dB squeezing for fault-tolerant quantum computation.

References

[1]	M. A. Nielsen and I. L. Chuang, “Quantum Computation and Quantum Information,” Cambridge University Press, 2010.
[2]	T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe, and J. L. O’Brien, “Quantum Computers,” Nature, Vol. 464, pp. 45–53, 2010.
[3]	S. Takeda and A. Furusawa, “Toward Large-scale Fault-tolerant Universal Photonic Quantum Computing,” APL Photonics, Vol. 4, No. 6, 60902, 2019.
[4]	W. Asavanant, Y. Shiozawa, S. Yokoyama, B. Charoensombutamon, H. Emura, R. N. Alexander, S. Takeda, J. Yoshikawa, N. C. Menicucci, H. Yonezawa, and A. Furusawa, “Generation of Time-domain-multiplexed Two-dimensional Cluster State,” Science, Vol. 366, pp. 373–376, 2019.
[5]	A. Furusawa, J. L. Sørensen, S. L. Braunstein, C. A. Fuchs, H. J. Kimble, and E. S. Polsik, “Unconditional Quantum Teleportation,” Science, Vol. 282, pp. 706–709, 1998.
[6]	W. Asavanant, B. Charoensombutamon, S. Yokoyama, T. Ebihara, T. Nakamura, R. N. Alexander, M. Endo, J. Yoshikawa, N. C. Menicucci, H. Yonezawa, and A. Furusawa, “Time-domain-multiplexed Measurement-based Quantum Operations with 25-MHz Clock Frequency,” Phys. Rev. Applied, Vol. 16, 034005, 2021.
[7]	T. Kashiwazaki, N. Takanashi, T. Yamashima, T. Kazama, K. Enbutsu, R. Kasahara, T. Umeki, and A. Furusawa, “Continuous-wave 6-dB-squeezed Light with 2.5-THz-bandwidth from Single-mode PPLN Waveguide,” APL Photonics, Vol. 5, No. 3, 036104, 2020.
[8]	D. Gottesman, A. Kitaev, and J. Preskill, “Encoding a Qubit in an Oscillator,” Phys. Rev. A, Vol. 64, 012310, 2001.
[9]	R. E. Slusher, L. W. Hollberg, B. Yurke, J. C. Mertz, and J. F. Valley, “Observation of Squeezed States Generated by Four-wave Mixing in an Optical Cavity,” Phys. Rev. Lett., Vol. 55, 2409, 1985.
[10]	U. L. Andersen, T. Gehring, C. Marquardt, and G. Leuchs, “30 Years of Squeezed Light Generation,” Phys. Scr., Vol. 91, 053001, 2016.
[11]	T. Umeki, O. Tadanaga, and M. Asobe, “Highly Efficient Wavelength Converter Using Direct-bonded PPZnLN Ridge Waveguide,” IEEE J. Quantum Electron., Vol. 46, No. 8, pp. 1206–1213, 2010.
[12]	N. Takanashi, T. Kashiwazaki, T. Kazama, K. Enbutsu, R. Kasahara, T. Umeki, and A. Furusawa, “4-dB Quadrature Squeezing with Fiber-coupled PPLN Ridge Waveguide Module,” J. Quantum Electron., Vol. 56, No. 3, 6000100, 2020.
[13]	T. Kazama, T. Umeki, S. Shimizu, T. Kashiwazaki, K. Enbutsu, R. Kasahara, Y. Miyamoto, and K. Watanabe, “Over-30-dB Gain and 1-dB Noise Figure Phase-sensitive Amplification Using a Pump-combiner-integrated Fiber I/O PPLN Module,” Opt. Express, Vol. 29, No. 18, pp. 28824–28834, 2021.
[14]	T. Kashiwazaki, T. Yamashima, N. Takanashi, A. Inoue, T. Umeki, and A. Furusawa, “Fabrication of Low-loss Quasi-single-mode PPLN Waveguide and Its Application to a Modularized Broadband High-level Squeezer,” Appl. Phys. Lett., Vol. 119, 251104, 2021.
[15]	H. P. Yuen and V. W. S. Chan, “Noise in Homodyne and Heterodyne Detection,” Opt. Lett., Vol. 8, No. 3, pp. 177–179, 1983.
[16]	N. Takanashi, A. Inoue, T. Kashiwazaki, T. Kazama, K. Enbutsu, R. Kasahara, T. Umeki, and A. Furusawa, “All-optical Phase-sensitive Detection for Ultra-fast Quantum Computation,” Opt. Express, Vol. 28, No. 23, pp. 34916–34926, 2020.