|
|||||||||||
|
|
|||||||||||
|
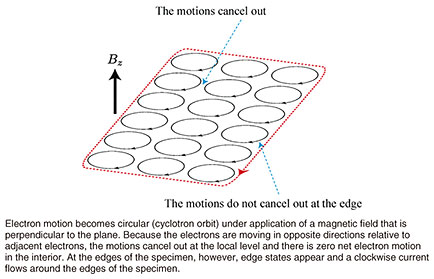
Feature Articles: Plasmon Control Technology Vol. 21, No. 5, pp. 30–33, May 2023. https://doi.org/10.53829/ntr202305fa4 Theoretical Proposal for Edge Magnetoplasmon CrystalAbstractWhen a static magnetic field is applied to a two-dimensional electron system, plasmons appear at the edge of the specimen and exhibit peculiar behavior, such as the wave propagation to a single direction along the edge. The calculated results of investigating plasmon propagation when a sample is divided into regions and a crystalline network is formed indicate that the characteristics of the integer/fractional quantum Hall effect, which has been developed in various fields, can be reproduced as optical properties. Keywords: plasmon, crystalline network, edge state 1. Directed wave propagationPropagating of light to a single direction is not straightforward because when there is a scatterer, light is reflected backwards, reversing the direction of propagation. To take advantage of straightness of light, we use the total reflection by materials such as in optical fibers. It is necessary to use the interaction between light and materials to improve the control of light. For the electrons in materials that emit light, however, such directed propagation can be achieved by applying a strong magnetic field perpendicular to a two-dimensional electron system.*1 The individual electrons in the system take on a circular trajectory, orbiting in a direction that is determined by the magnetic-field vector (cyclotron motion, Fig. 1). As is easily visualized on the microscopic level, adjacent electrons move in opposite directions, thus cancel out on the macroscopic level, leaving substantial current produced by many electrons only at the edges of the specimen. This situation is referred to as an edge state and forms a propagation channel along the edge. The propagation direction in the edge state is either clockwise or counterclockwise, depending on the vector direction of the applied magnetic field. What happens when the edge state is excited has been studied since the 1980s. An excited state is a hybrid of electrons and electromagnetic field, and it propagates in a single direction along the specimen edge. It is called an edge magnetoplasmon, because it is a plasmon created at the edge by an external magnetic field.
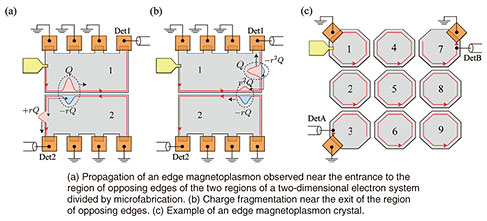
2. Charge fractionalizationAn interesting question is what would happen if a single system in which edge magnetoplasmons circulate is divided into two regions by microfabrication. We divide a specimen into two parts as shown in Fig. 2, where the upper part is region 1 and the lower part is region 2. We assume that edge magnetoplasmons exist on the edges of regions 1 and 2 and that the plasmons propagate counterclockwise. In the groove between the two specimens, there are counterpropagating channels (like parallel roads or train tracks) that interact if they are close enough to each other through the electromagnetic interaction (Coulomb potential). Suppose we excited the magnetoplasmon in region 1. Upon reaching the coupled region, a gradation in the charge density (positive and negative charge pair) is formed in region 2, where there had been nothing (Fig. 2(a)). Denoting the charge of the edge magnetoplasmon excited in region 1 as Q, the charge generated at the entry of the coupled region in region 2 can be denoted as
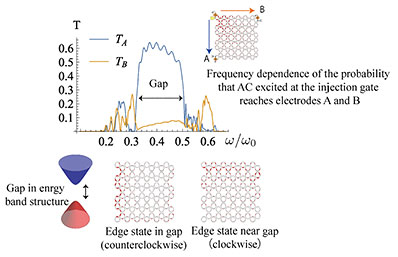
When the composite pulse reaches the exit of the opposing region, the –rQ component in region 2 loses the attraction of the partner in region 1, and its motion reverses to the normal direction. A charge pair 3. Edge magnetoplasmon crystalMy current research is an extension of the problem described above, where I considered what phenomena or capabilities appear when a two-dimensional semiconductor is divided into many elements by using microfabrication techniques to produce a semiconductor “crystal” network (for example, a crystal that comprises several “atoms,” as shown in Fig. 2(c)). Such problems are a natural direction for extended research. In nanocarbon research, for example, there is a history of increasing the network periodicity of benzene rings from C60 fullerene to planar graphene systems. However, this is not the only motivation. There is also understanding the electronic properties of two-dimensional semiconductors subjected to strong magnetic fields from a perspective that is closer to light and applying that understanding to new areas. For example, assuming the degree of fragmentation to be the diameter of the cyclotron motion, the situation can be regarded as a plasmon optical simulation of a quantum Hall system. One interesting topic is the conditions under which edge magnetoplasmons appear (coupling strength and crystal shape). I believe that the differences between the two types of quantum Hall effects (integer and fractional) can be understood from the viewpoint of edge magnetoplasmons. The integer Hall effect is thought to originate in a single-electron scenario where impurities cause scattering. The fractional Hall effect is believed to result from a many-body effect produced by the interaction between electrons. For edge magnetoplasmon crystals, scattering is caused by defects in the network, and r can serve as a parameter for the electron interaction. I first calculated the energy band structure of an edge magnetoplasmon to understand the characteristics of propagation through the domain crystal [2]. The details are omitted here, but I used the transfer matrix method for a periodic network without edges. The band structure is a plot of natural frequency versus wavelength and is useful for understanding the state of a crystal. If there is no eigenfrequency for any wavelength within a band, it is referred to as an energy gap within which there is no state for propagation. The calculation results for a honeycomb network of hexagonal “atoms” indicate a band structure that includes energy gaps (Fig. 3). The size of the gap between the two cones tends to increase with r indicating an interaction-induced energy gap. In the original specimen prior to splitting, the edge magnetoplasmons appeared in the energy gap created by quantization*2 of the cyclotron orbits (Fig. 1). That gap was not created by interaction, so gaps in edge magnetoplasmon crystals have a different origin from the original edge magnetoplasmons.
Although I learned that energy gaps also appear in an edge magnetoplasmon crystal, I do not know from the band structure alone (calculation results obtained under the assumption of a periodic edgeless system) whether there are edge modes that propagate along the network edge within those gaps. A more detailed analysis revealed that there are edge modes (Fig. 3). This means that edge magnetoplasmons also exist in edge magnetoplasmon crystals. Interestingly, a mode that moves in the direction opposite normal edge propagation appears at frequencies near the band-gap margins. It is known that edge-state propagation can be bidirectional in the fractional quantum Hall effect. If we consider the interaction between “atoms,” the fractional quantum Hall effect caused by the many-body effect can also be taken into account in the calculation. This can be interpreted as the appearance of a mode that propagates in the opposite direction.
4. Conclusion and future prospectsOur understanding of the physical properties of two-dimensional electron systems has undergone broad development, ranging from basic research, such as linking to mathematical topology, to application. The potential of applying this understanding to improving light manipulation is clear. However, the energy scales of electronic states and optical states are generally far apart (the telecommunications wavelength band, for example), and finding a direct link between the two is a difficult problem that requires a new approach. Many researchers are interested in the fusion of the behaviors of light and electrons to produce new capabilities. Inspired by plasmons as a hybrid optoelectronic state, I am searching for such a new approach, and an edge magnetoplasmon crystal is a likely candidate for this purpose. The quantum mechanical behavior of photons at low light intensity has also attracted much interest. The quantum mechanics of edge magnetoplasmons has also been extensively studied, and one topic for future work is the quantum field theory*3 of edge magnetoplasmon crystals.
References
|
|||||||||||