Analysis of Complex Data Based on
C^*-algebra and Operator Theory to Explain Unknown Phenomena in Data Analysis Using Mathematical Theories

Applying advanced mathematical theories to data analysis to solve social problems in diverse fields including communications

—Dr. Hashimoto, what type of technology is “analysis of complex data based on C^*-algebra and operator theory”?

Analysis of complex data based on C^*-algebra and operator theory is technology for expressing and analyzing complex data using the concept of an “operator” as a generalized matrix. To give some background on the need for this technology, automating the operation of current information and communication technology (ICT) systems requires the analysis of data that behaves in complex ways such as “data with noise” or “mutual interaction between multiple items of data and continuous change.” For example, in network communication traffic, the mutual interaction of communication traffic at various locations must be simultaneously considered such as “when traffic increases at point A, the traffic at point B also increases.” In addition, when investigating the state of equipment and devices, different types of data must be simultaneously considered such as CPU (central processing unit) usage and memory usage. Moreover, when constructing a learning model using a current neural network, a large amount of data is needed, but in actuality, there are cases in which a highly accurate learning model cannot be constructed due to an insufficient amount of data, so there is a growing demand for technology that can perform analysis with high accuracy even with a small amount of data.

In response to this problem, a mathematical theory that has been commonly used up to now involves the observing of a single value (scalar value) such as a real number or complex number. In contrast, analysis of complex data based on C^*-algebra and operator theory proposes a new framework for data analysis that uses advanced mathematical theories such as C^*-algebra and operator theory to integrate (make continuous), abstract, and simplify models or data. If we apply to data analysis the property in which an object can be considered to have multiple values simultaneously as an extension of conventional theories, multiple values can be extracted from one type of data when analyzing data, thereby enabling high-efficiency, high-accuracy data analysis.

My research into this technology of analysis of complex data based on C^*-algebra and operator theory came about when I had been toying with the idea that matrices or mathematical concepts extending matrices could be used to good effect for analyzing the relationships among multiple data items. Then, on being taught about C^*-algebra from my co-researchers, I began to apply it in earnest. Mathematical theories used in analysis of complex data based on C^*-algebra and operator theory are not limited to specific application fields. Rather, as a framework, they are very general in nature, which means that they can be deployed in a variety of fields beyond communications and ICT systems. I am also studying whether problems can be solved by using a continuous framework to represent time-series-like changes as in the propagation of light. For example, in studies that I am now conducting, I’m using this research to analyze biological data such as the brain waves and body temperature of animals in the natural world. In addition, using data that has been analyzed with high accuracy should make it possible to detect anomalies such as disasters or faults beforehand or to mount responses to unknown anomalies based on communication traffic and signals. In this way, I am conducting interdisciplinary research in machine learning, mathematics, physics, biology, and quantum mechanics and other fields regardless of the framework of communications. My target here is a comprehensive approach beyond traditional field boundaries to enhance industry and explain natural and social phenomena (Fig. 1).

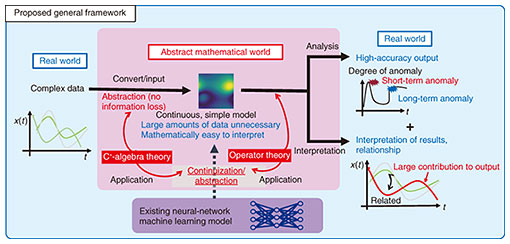
Fig. 1. Overview of analysis of complex data based on C^*-algebra and operator theory.

—Please explain the specific technique behind analysis of complex data based on C^*-algebra and operator theory.

In analysis of complex data based on C^*-algebra and operator theory, data that continuously changes over time is treated as a mathematical object for analysis. When analyzing time-series data by conventional means, data at different times are treated as a collection of separate “points.” In contrast, treating that data as a mathematical object called a function, that is, as a “line,” enables data analysis on a more advanced level.

In addition, high-accuracy analysis even with a small amount of data becomes possible by finding values such as eigenvalues or singular values that characterize that data. In existing research, such values have been found by abstracting the data to convert it to mathematical information and to then return it to discrete values to extract approximate features. This technique, however, has a drawback in that the properties of the data are lost and the accuracy of the analysis drops. In analysis of complex data based on C^*-algebra and operator theory, I have been working on a technique for analyzing data continuously while preventing a loss of information as much as possible. A technical issue here is that the property of being continuous (infinite dimensional) is completely different from the property of being discrete (finite dimensional) and that unimaginable concepts from each dimension frequently arise. This makes it difficult to analyze data simply by attempting to extend discrete data to continuous data, so I am studying the application of advanced mathematical knowledge to determine how best to extend present concepts. Handling data in continuous form requires advanced mathematical knowledge, so at present, I myself can proceed with my research with the help of many experts.

—Are there any difficult points to deal with in your research of analysis of complex data based on C^*-algebra and operator theory?

A major problem is how to link data in the real world with the theoretical world of mathematics. For example, in neural-network analysis, neural networks are studied as a simple structure having a form that is easy to mathematically describe in theory. However, to completely reproduce an actual and complex neural network, a variety of operations are needed such as data processing or the cutting of values during the information-processing step, which at present is not fully reflected in neural networks. Improving accuracy by performing such detailed operations has actually been demonstrated by experimental results. My current aim therefore is to construct a high-accuracy neural network by newly conducting as many studies as possible on two key points. These are “what kind of mechanism does a neural network use to operate,” and once that is explained, “how can accuracy be further improved.” In this regard, given that there are many cases in data analysis that can be thought of as simple in theory, I would like to make every effort in the construction of a technique using theoretical analysis and mathematical theories to enable data analysis while incorporating many realistic settings.

In addition, I pay particular attention to guaranteeing theoretical accuracy in my research. In the case of neural networks, for example, a data model used in training may fit a certain type of data thereby raising the accuracy of data analysis, but there are cases in which the same model does not fit other types of data resulting in a drop in accuracy. Of course, in actual research, this can happen even for results described in a paper. Even if a paper states that “XX% accuracy was achieved using this data,” it cannot necessarily be guaranteed that a similar improvement in accuracy can be expected when actually attempting to use that technology with one’s own settings. It often happens that changing the data changes the results, so to prevent such a problem from occurring, it is necessary to place importance on theoretically investigating beforehand whether high-accuracy data analysis can be performed for all sorts of data. In this way, it is easy to make this technology attractive even to people accustomed to using technology—I feel that it’s an important undertaking to get people to understand that this technology can be used without worry.

Toward research that places importance on collaboration with other fields while having a broad perspective

—Going forward, what is your research vision for analysis of complex data based on C^*-algebra and operator theory?

My research vision for the future is to apply this technology to a variety of fields requiring the analysis of complex data, including communication networks, with the aim of solving many social problems. For example, given that light changes continuously, I believe that explaining the properties of light using the framework of analysis of complex data based on C^*-algebra and operator theory can contribute to the development of NTT’s Innovative Optical and Wireless Network (IOWN).

In addition, problems analyzed in biology have features similar to those of data analysis in communication networks, so as a new research vision to pursue from here on, I would like to explain certain animal properties such as animal sleep in coordination and cooperation with experts in biology. A mathematical framework used in analysis of complex data based on C^*-algebra and operator theory is very general in nature, so I would like to broaden my collaboration with people in diverse fields. Thinking that I can apply this technology to problems in various fields and thereby unite issues that up to now have been studied separately, my aim is to help find solutions to diverse problems in industry and the natural world (Fig. 2).

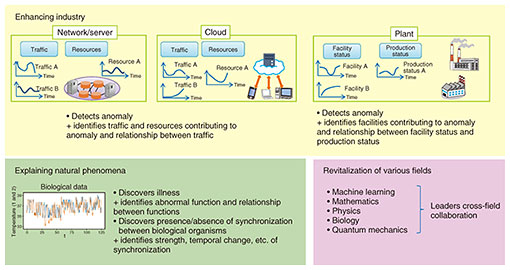
Fig. 2. Application examples of analysis of complex data based on C^*-algebra and operator theory.

—Dr. Hashimoto, please leave us with a message for researchers, students, and business partners.

In my research of analysis of complex data based on C^*-algebra and operator theory, I have been working to bridge the gap between application and theory in mathematics. For this reason, there have been many opportunities to conduct research together with a variety of people and there have been many occasions to share results within the company. In such an environment, research being conducted by a small group of people can be shared with another group in the manner, for example, of “I wonder if this technology could be used here as well?” In this way, getting an idea about an application that you have not thought of is very beneficial and can also generate a moment of joy in your research activity. Therefore, I place great importance on pursuing my research while interacting with many people.

NTT conducts a wide range of research from basic research to applied research, and NTT Network Service Systems Laboratories that I belong to works on both application and theory, which makes it a very attractive environment. For example, talking with the people around me involved in actual development enables me to learn quickly about their goals and actual problems and to receive comments from an academic point of view. This helps me to move my research forward. To give an example of this, the department that I belong to researches and develops fundamental technologies for the automation of ICT system operations, so I am surrounded by colleagues having a wealth of knowledge and diverse backgrounds, which gives me daily inspiration in my research.

Of course, specializing in one field is important for a researcher, and your field should not be ignored. On the other hand, you may miss many things by focusing excessively on only one field. In research, it is important to have a broad perspective, so I try to stay active without being stuck in one field as much as possible. To be sure, an environment that promotes joint research with people in related fields makes it easy to obtain an understanding of one’s surroundings and to communicate with others, which facilitates research. Yet, by taking a step outside one’s everyday environment and listening to people in other fields or participating in academic societies in fields different than usual, you should be able to obtain new ways of looking at things that you had not thought about before. I myself, by cooperating with people in other fields different from those I had so far been exposed to, I have noticed mistakes in my own way of thinking, and when talking to people in other fields and not being able to communicate at all, I have become aware that “I have been thinking in only a very narrow space.” I feel that experiences such as these are a huge plus for a researcher.

Taking a step forward by oneself into a new area is difficult, but I think that an interesting world that you have never seen before waits for you there. I too would like to broaden my field of view even further from here on, and to everyone reading this, I would like to ask you first and foremost to try talking to people in fields different than your own. This will open new doors for you!