|
|||||||||||
|
|
|||||||||||
|
Feature Articles: Efforts to Speed Up Practical Application of Quantum Computers Vol. 21, No. 11, pp. 23–28, Nov. 2023. https://doi.org/10.53829/ntr202311fa2 A Computing System for Supporting Application Development Using Ising MachinesAbstractOne of the problems that conventional computers, such as those based on central processing units, cannot solve is the combinatorial optimization problem, the solution to which is a pattern from among a huge number of combinations of patterns that satisfies a certain condition. Operating on the basis of a new principle, an Ising machine is a computer that specializes in solving this problem. However, there are many challenges to using an Ising machine, such as converting real-world problems into a format that the Ising machine can handle. Research and development of a software development kit and computing system that overcome these challenges are introduced in this article. Keywords: Ising machine, LASOLV™, combinatorial optimization problem 1. Combinatorial optimization problems and Ising machinesCombinatorial optimization problems, namely, finding the best solution from a large number of alternatives, are difficult to solve and require long computation time even with today’s computers. For example, the traveling salesman problem (finding the most-efficient order in which to visit multiple destinations) and the graph-coloring problem (ensuring that adjacent areas of a given map are painted with different colors under the constraint of a limited number of colors) are typical combinatorial optimization problems that become more difficult as the scale of the problem increases. Research on an Ising machine that solves such problems on the basis of a new approach, namely, using a model representing the properties of magnetic materials, is progressing. An Ising machine is a computer that specializes in solving a combinatorial optimization problem called the Ising-model ground-state search problem. As a statistical-mechanics model, an Ising model describes a network of magnets (each with a property called “spin”), as shown in Fig. 1. The spin σi can be either up (+1) or down (–1). If Jij and hi represent spin-spin interaction and magnetic-field strength, respectively, the ground state is the state in which the second-order polynomial Ising model H, defined by the following equation, is minimized.
The combination of spins that satisfies this equation is the solution to the ground-state search problem.
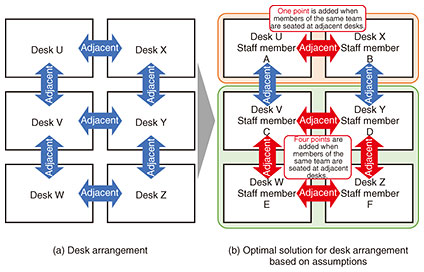
Although there are many different types of combinatorial optimization problems, it has been theoretically proven that they can all be transformed into such an Ising-model ground-state search problem. Given this fact, various companies, such as D-Wave Systems [1] and Fujitsu [2], have developed Ising machines and are using them to solve various combinatorial optimization problems. Likewise, NTT laboratories are developing a laser-based coherent Ising machine [3] called LASOLV™. 2. Software development kit to facilitate the use of Ising machinesTo use an Ising machine, it is necessary to represent the problem to be solved in the form of an Ising model that can be input to the Ising machine. To express the problem with the Ising model, it is necessary to (i) correlate the value taken by the spin (+1 or –1) and the meaning of the solution to the problem and (ii) create a polynomial that corresponds to the desired solution when the value of the Ising model is minimized. The reason for correlating that minimum value to the desired solution is that the Ising machine is a calculator that finds the value of spin at which the input Ising model is minimized. The task of devising the Ising model becomes more complicated in proportion to the complexity of the problem, which increases the difficulty of using the Ising machine. NTT Computer and Data Science Laboratories is developing a software development kit (SDK)—called cimsdk—that greatly simplifies the process of devising Ising models. The conventional process for devising an Ising model is explained as follows with a simple problem as an example. In this example of an office department, six staff members (given as A, B, C, D, E, and F) are to be assigned to six desks (given as U, V, W, X, Y, and Z). The six desks are positioned, as shown in Fig. 2(a). It is assumed that one desk must be assigned to one staff member (Assumption 1). It is also assumed that staff members A/B and C/D/E/F are teamed up for the same job, so they must be assigned adjacent desks. In this process, one point is added to a points total when each staff-member pair on the same team is assigned adjacent desks, and the goal is to maximize the total number of points (Assumption 2). Based on Assumptions 1 and 2, the assignment shown in Fig. 2(b) is one of the solutions giving the maximum number of points. The following Ising-model representation of this example problem is considered.
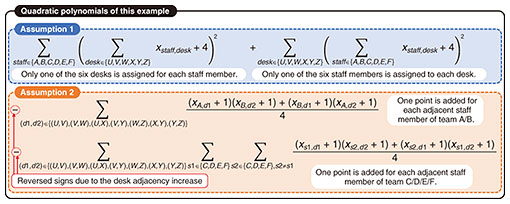
First, the correspondence between the +1 and –1 spins and the meaning of the solution to the problem are considered. One spin is assigned to each of the 36 possible combinations of 6 staff members and 6 desks, and the following meaning is associated with each spin: “+1 means that a certain staff member was assigned to a certain desk” and “–1 means that the staff member was not assigned to that desk.” The spins are represented by variable xA,U, where A represents the staff member and U represents the desk. For example, xB,X is interpreted as follows: “If x is +1, staff member B was assigned to desk X; if x is –1, staff B was not assigned to desk X. For the 36 spins prepared in this way, the following expressions for Assumptions 1 and 2 are considered. Assumption 1 (i.e., one desk per staff member) is supposed to express spin as described earlier. In other words, “only one of the six desks is assigned to each staff member” or “only one of the six staff members is assigned to each desk.” For example, the assumption “only one of the six desks is assigned for staff member A” can be expressed by the quadratic polynomial (∑desk∈{U,V,W,X,Y,Z} xA,desk + 4)2. The value of this quadratic polynomial is minimized when only one of xA,U – xA,Z is +1 and the remaining five variables are –1. The fact that only one desk is assigned to a staff member corresponds to the fact that the value of the quadratic polynomial is minimized. The other staff members and desks can be represented by a similar quadratic polynomial with a single assignment. Assumption 2 (i.e., 1 point is added for each staff member of the same team seated at adjacent desks) is considered with the following example of a team composed of staff members A and B. One point is added if staff members A and B are respectively assigned to desks U and X. Assumption 2 is expressed as the quadratic polynomial (xA,U + 1)(xB,X + 1)/4. When +1 and –1 are respectively substituted for xA,U and xB,X, this quadratic polynomial is +1 only when xA,U and xB,X are +1; otherwise, it is 0. Since this condition would result in no points being awarded for opposing desk assignments and/or combinations of non-team staff members on adjacent desks, the number of points awarded can be expressed as a quadratic polynomial by adding up the values given by the quadratic polynomials for all combinations. It should be noted that the Ising machine derives the solution that minimizes the Ising model. In other words, it is necessary to minimize the value taken by the Ising model as the points added due to the desk adjacency increase, so the plus or minus signs of these quadratic polynomials are inverted, and these quadratic polynomials are added together. The Ising model for this example is shown in Fig. 3, which is constructed by adding up the above-devised quadratic polynomials. Even in the case of such a simple example, the Ising-model formula/equation is relatively complex.
In contrast, the Ising model constructed using the functions of cimsdk is shown in Fig. 4. It can be understood that the Ising model can be generated without considering what value each polynomial takes when it satisfies what, which was a necessary condition when devising the equations in Fig. 3.
For practical problems, more spins and more complex assumptions are required, so the task of devising an Ising model becomes much more complicated. Practical problems may deal with integers, and it may be necessary to combine multiple spins taking either +1 or –1 and treat them as a single integer. If it is necessary to express conditions related to three or more spins at the same time, it will be necessary to handle third-order or higher polynomials; however, the Ising model can only handle second-order polynomials, so the polynomial order must be reduced. Regarding the work of devising such a complicated Ising model, cimsdk provides a function for automatically converting various spins (such as integers and their related conditions) to the Ising model. This function makes it easy for people without expertise in Ising models or Ising machines to benefit from the fast solutions given by the Ising machine. The unique strengths of cimsdk in comparison with similar SDKs from other companies are three-fold: (i) the ability to combine multiple conditions unrestrictedly, (ii) the ability to express mathematically definable logical structures as is, and (iii) the ability to automatically generate the corresponding Ising model from an arbitrary associative array. We plan to expand the number of spins and conditions for automatic conversion to an Ising model, thereby broadening the range of practical problems that can be handled by cimsdk. 3. Application development and execution using LASOLV™ computing systemAnother problem with using an Ising machine is that it is difficult for it to complete the application because it is a computer specialized for solving the Ising-model ground-state search problem. To execute processes, such as data pre-processing and post-processing using cimsdk, for classical computers to have an advantage, a heterogeneous system that combines an Ising machine with various computing devices, such as classical computers, is required. The cost and installation location of an Ising machine pose difficulties compared with those of a personal computer or a general server, so it is difficult to have a large number of Ising machines available. Therefore, as is the case with supercomputers, a means of sharing a small number of Ising machines among several users is required. NTT Computer and Data Science Laboratories has therefore been developing the LASOLV™ Computing System (LCS) as a platform for efficient use of Ising machines such as LASOLV™ [4]. In addition to providing a development environment that facilitates application development such as cimsdk, LCS has functions for controlling user jobs and scheduling them so that multiple users’ jobs do not overlap while efficiently coordinating and using nodes that perform calculations on central processing units and Ising machines. By developing applications using cimsdk on LCS, we are also developing applications that use the capabilities of LASOLV™. To cite an example, we conducted a joint demonstration in conjunction with Mitsubishi Heavy Industries, Ltd. to use an Ising machine for personnel-assignment planning [5]. The company is responsible for inspecting and repairing power plants and other facilities worldwide. In response to this responsibility, workers with skills tailored to various inspection items must be dispatched, and personnel-assignment plans must account for complex parameters such as the number of workers, consecutive working days, and overtime hours. Conventionally, it took about one month for a skilled planner to manually formulate a personnel-assignment plan for 26 plants to be inspected by 141 workers within a period of 64 days to find a candidate solution for the plan that satisfies constraints such as the skills possessed by the workers. The scale of this task is tremendous, namely, 3.48 × 1013329 combinations. By using the latest version of LASOLV™, which can calculate 50,000 spins at once, we demonstrated that a solution can be obtained in a very short time. This high solution speed is expected to make it possible to formulate personnel-assignment plans with multiple patterns and revise the plans as needed to accommodate infectious-disease countermeasures and other circumstances. 4. Future developmentsOur efforts concerning SDKs to facilitate application development and computing-system development while taking into account the characteristics of Ising machines were introduced. Practical application of quantum computers—as well as Ising machines—will increase the importance of SDKs and other libraries that account for their characteristics, and the need for computing systems with greater heterogeneity will grow. At NTT Computer and Data Science Laboratories, we will define the ideal computing-system architecture that uses advanced technologies, such as quantum computers and advance research, on that architecture. References
|
|||||||||||