
You need Adobe Reader 7.0 or later in order to read PDF files on this site.
If Adobe Reader is not installed on your computer, click the button below and go to the download site.

|
Regular Articles
Vol. 23, No. 9, pp. 48–55, Sept. 2025. https://doi.org/10.53829/ntr202509ra1
Compositional Abilities Emerge Multiplicatively: Exploring Diffusion Models on a Synthetic Task
Maya Okawa and Hidenori Tanaka
Abstract
Modern generative models exhibit remarkable abilities to produce realistic data. However, for practical use, they must reliably compose new combinations of concepts to generate outputs unseen during training, reflecting real-world compositionality. Prior research shows that diffusion models exhibit intriguing yet inconsistent compositional generalization abilities in text-to-image generation tasks. Motivated by these findings, we conduct a controlled study to investigate compositional generalization in diffusion models using synthetic tasks. By systematically varying training data attributes, we measured models°« capacities to generate out-of-distribution samples. Our results reveal three key insights: (i) compositional ability emerges according to the underlying data-generation structure; (ii) compositional-task performance shows sudden °»emergence°… due to multiplicative dependencies on constituent tasks, clarifying emergent behaviors in generative models; (iii) generating out-of-distribution samples from rarely encountered concept combinations requires significantly more optimization steps compared with generating familiar combinations. Our findings establish a data-centric framework for understanding emergent compositional capabilities in generative models.
Keywords: text-to-image model, diffusion model, synthetic task
1. Introduction
The scaling of data, models, and computation has unleashed powerful capabilities in generative models, enabling controllable synthesis of realistic images [1–3] and videos [4, 5], accurate image editing [6–8], and semantically coherent text generation [9, 10]. With increased interest in incorporating these models in day-to-day applications [11, 12], e.g., to improve robotic systems via better planning and grounding [13–15], analyzing and improving their reliability has become crucial.
With the motivation above, we investigate compositional generalization abilities of conditional diffusion models, i.e., diffusion models that are conditioned on auxiliary inputs to control their generated images (e.g., text-conditioned diffusion models [16, 17]). Given the inherent compositionality of the real world, it is difficult to create a training dataset that exposes a model to all combinations of different concepts underlying the data-generating process. We therefore argue that compositional generalization is central to model reliability in out-of-distribution scenarios, i.e., when the model has to compose a novel set of concepts to generate outputs not seen in the training dataset [18, 19]. As several studies investigating the compositional generalization capabilities of off-the-shelf text-conditioned diffusion models [20–23] have shown, modern diffusion models often compose complicated concepts, producing entirely non-existent objects but unpredictably fail to compose apparently similarly complicated concepts (see Fig. 1). It remains unclear why models produce novel samples by composing some concepts but not others. What concepts does a model learn to compose? What differentiates these concepts from the ones the model is unable to compose?

Fig. 1. (Lack of) Compositionality in text-conditioned diffusion models. Images generated using Stable Diffusion v2.1. We see diffusion models conditioned on text descriptions of the concepts in an image often allow generation of novel concepts that are absent from the training data, indicating an ability to compose learned concepts and generalize out-of-distribution (lizard and goldfish panels). However, the model sometimes unpredictably fails to compose concepts it has learned, i.e., compositional capabilities depend on the specific concepts being composed. For example, generating a panda in this figure is difficult for the model, likely because it has not been exposed to different colors of pandas. The model instead alters the background or lighting to change the color.
1.1 Model experimental systems approach with interpretable synthetic data
To address the above questions, we seek to take a systematic approach to understanding complex systems, such as generative models, by dividing the process into hypothesis generation and testing. Drawing inspiration from the natural sciences, we adopt a model experimental systems approach, which involves studying simplified, controllable, and steerable experimental systems to develop mechanistic hypotheses applicable to more complex systems. For instance, in neuroscience research, model organisms, such as mice or fruit flies, are used to study neural mechanisms and develop hypotheses that can be tested on the larger-scale human brain [24, 25]. Similarly, we design a synthetic experimental setup that pursues simplicity and controllability while preserving the essence of the phenomenon of interest, i.e., compositional generalization. Our data-generating process attempts to mimic the structure of the training data used in text-conditioned diffusion models by developing pairs of images representing geometric objects and tuples that denote which concepts are involved in the formation of a given image (see Fig. 2). We train diffusion models on synthetic datasets sampled from this data-generating process, conditioning the model on tuples denoting which concepts an object in the image should possess, while systematically controlling the frequencies of concepts in the dataset. We then investigate the model’s ability to generate samples corresponding to novel combinations of concepts by conditioning the denoising process on a correspondingly novel tuple, thus assessing the model’s ability to compositionally generalize. This approach allows us to systematically investigate the key properties of a dataset, enabling compositional generalization in an interpretable and controlled manner in conditioned diffusion models.
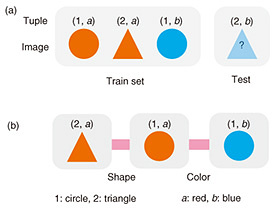
Fig. 2. Compositionality in a minimalistic conditional generation task. (a) We train diffusion models on pairs of images and tuples, where the tuples denote the values of the concepts represented in the image (e.g., values of color and shape in the figure). (b) Samples between which only a single tuple element differs simplify the learning of a capability to recognize and alter the concept distinguishing the images. To test the existence of such capabilities of a trained model, we ask the model to generate images corresponding to novel tuples that are out-of-distribution, hence requiring compositional generalization.
Our main contributions are as follows.
- Concept graphs: A simple, synthetic framework for studying conditional diffusion models. We develop a minimalistic abstraction for training conditional diffusion models by introducing a framework called concept graphs. The framework forms the foundation of our systematic study of how diffusion models learn to generate samples from a set of concepts and compose these concepts to generate out-of-distribution samples. To our knowledge, our results are the first demonstration of perfect compositional generalization on a (synthetic) vision problem.
- Multiplicative emergence of compositional abilities. We use our model system’s interpretability to monitor learning dynamics of a diffusion model’s capabilities and the ability to compose them to produce out-of-distribution data. As we show, a diffusion model first memorizes the training dataset then sequentially generalizes to concepts that are at a greater “distance” from the training distribution. Since progress in learning each capability multiplicatively affects the model’s performance in compositional generalization, we find that a sudden ability to compose and produce samples out-of-distribution “emerges.” We thus hypothesize compositionality may partially explain emergent phenomena seen in modern generative models [26, 27].
- Investigating challenges for compositional generalization. We systematically examine the challenges arising from decreased frequency of specific concepts necessary for learning a corresponding capability. We further evaluate the effectiveness of using fine-tuning to address misgeneralizations in adversarial settings, and find that it generally insufficient to enable the learning of new capabilities.
2. Concept graph: A minimalistic framework for compositionality
In this section, we present the concept graph framework, as shown in Fig. 3, which enables us to visually depict the compositional structure of our synthetic data and forms the basis for generating hypotheses and designing experiments in our work. We begin by defining the essential building blocks of our framework: concept variables and concept values. In the following, we call a specific output of our data-generating process an “object” (see Fig. 3).
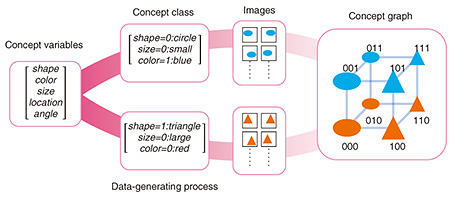
Fig. 3. Concept graphs. We organize our study using a simple but expressive framework called concept graphs. The basis of a concept graph is a set of primitives called concept variables (e.g., shape, color, etc.). A subset of these variables is instantiated with specific values to yield a concept class, e.g., shape=0, size=0, color=1 indicates a small, blue circle. This is akin to defining a broad set of objects that share some common properties, e.g., all lizards in Fig. 1 belong to the same species, despite their diverse colors. A specific object in this class is instantiated by fixing the remaining variables, e.g., small, blue circles at different locations. Each concept class corresponds to a graph node, where nodes are connected if their concept classes differ by a concept distance of 1.
Definition 1. (Concept variables). A concept variable vi uniquely characterizes a specific property of an object. We denote V = {v1, v2, …, vn} a set of n concept variables, such that, given an object x, vi(x) returns the value of the ith concept variable in that object.
For instance, for geometric objects shown in Fig. 3, concept variables may include shape, color, size, and angle. These variables take on values from a pre-specified range, called concept values, as described below.
Definition 2. (Concept values). For each concept variable vi ∈ V, Ci = {ci1, ci2, …, ciki} denotes the set of ki possible values that vi can take. Each element of Ci is called a concept value.
For example, in Fig. 3, the concept values for the shape variable are in the set {circle, triangle, square}, while for the color values are in the set {red, blue, green}. Given n concept variables, with each vi having ki concept values, there can be 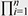 ki distinct combinations that yield a valid object. We use a unique combination of a subset of these concept variables, v1, …, vp (p < n), to define the notion of a concept class. ki distinct combinations that yield a valid object. We use a unique combination of a subset of these concept variables, v1, …, vp (p < n), to define the notion of a concept class.
Definition 3. (Concept class). A concept class C is an ordered tuple (v1 = c1, v2 = c2, …, vp = cp), where each ci ∈ Ci is a concept value corresponding to the concept variable vi. If an object x belongs to concept class C, then vi(x) = ci ∀i ∈ 1, …, p.
Note that the remaining n – p concept variables are free in the above definition. When these free variables are specified, we obtain a specific object from our data-generating process. That is, a concept class represents a family of objects by specifying the values of a pre-defined subset of concept variables. For example, in Fig. 1, different colored lizards instantiate images (objects) from the species (concept class) of lizards; the color of the lizard serves as a free variable. Similarly, in the geometric-objects scenario of Fig. 3, a “small red circle” would be a concept class for which the shape, color, and size variables have been assigned specific values. Objects are images designated by associating precise values with the remaining concept variables of location and angle. Next, we introduce the notion of concept distance, which serves as a proxy to succinctly describe the dissimilarity between two concept classes.
Definition 4. (Concept distance). Given two concept classes C(1) = 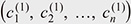 and C(2) = and C(2) = 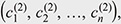 the concept distance d(C(1), C(2))
is defined as the number of elements that differ between the two concept classes: d(C(1), C(2)) = the concept distance d(C(1), C(2))
is defined as the number of elements that differ between the two concept classes: d(C(1), C(2)) = 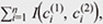 where I(c1i, c2i) = 1 if c1i ≠ c2i and I(c1i, c2i) = 0 otherwise. where I(c1i, c2i) = 1 if c1i ≠ c2i and I(c1i, c2i) = 0 otherwise.
The concept distance quantifies the dissimilarity between two concept classes by counting the number of differing concept values. It is important to note that this distance serves only as a null model because each axis represents distinct concept variables, and each of the variables can assume various possible concept values. We are now ready to define the notion of a concept graph (see Fig. 3), which provides a visual representation of the relationships among different concept classes.
Definition 5. (Concept graph). A concept graph G = (N, E) consists of nodes and edges, where each node n ∈ N corresponds to a concept class, and an edge e ∈ E connects two nodes n1 and n2 representing concept classes C(1) and C(2), respectively, if the concept distance between the two concept classes is 1, i.e., d(C(1), C(2)) = 1.
A concept graph organizes different concept classes as nodes in the graph, while edges denote pairs of concept classes that differ by a single concept value. An ideal conditional diffusion model, when trained on a subset of the nodes from this graph, should learn capabilities that enable it to produce objects from other concept classes.
2.1 Experimental and evaluation setup
With the concept-graph framework in place, we now have the tools to systematically investigate the impact of different data-centric properties on learning and composing capabilities in conditional diffusion models. Before proceeding, we briefly define our experimental setup and evaluation protocol. This enables us to interleave our results with our hypotheses, explaining them in context.
Experimental setup. We train conditional diffusion models with U-Net [1]. Our dataset involves concept classes defined using three concept variables, each with two values, shape = {circle, triangle}, color = {red, blue}, and size = {large, small}. Tuples with binary elements are used to condition the diffusion model’s training; they serve as an abstraction of text conditioning. For example, the tuple 000 indicates a large, red circle is present in the image. To sample images from this process, we simply map the size and color axes to the range [0,1] and uniformly sample to develop a training dataset of 5000 samples; the precise samples depend on which concept classes are allowed in the data-generating process.
Evaluation metric. Evaluating whether a generated image corresponds to the desired concept class might require a human in the loop. We use the diffusion-model training data to train three linear probes, which respectively infer the following three concept variables: shape, color, and size. We define a model’s accuracy for generating images of a given concept class as the product of the probabilities outputted by the three probes that each concept variable matches the value for the concept class. Note that a random classifier for a concept variable will have an accuracy of 0.5. We indicate this random baseline with dotted, gray lines in our plots when useful.
3. Multiplicative emergence of compositional abilities
We first investigate the order in which a model learns capabilities to produce sample from a concept class and how the learning of such capabilities affects the ability to compositionally generalize.
3.1 Learning dynamics respect the structure of the concept graph
We find the ability to compositionally generalize—i.e., produce samples from out-of-distribution concept classes—emerges at a rate that is inversely related to a class’s concept with respect to classes seen in training. Figure 4(a) shows the learning dynamics of the model, where light blue nodes denote concept classes within the training dataset, while pink and dark pink nodes respectively denote classes at concept distances of 1 and 2 from classes in the training dataset. As the model learns to fit its training data (light blue nodes), it learns capabilities that can be composed to produce samples from out-of-distribution concept classes (pink/dark pink nodes). Figure 4(b) further shows that the learning dynamics of compositional generalization are impacted by the concept distance from the training set: the model first learns the concept classes in the training dataset (light blue lines) then generalizes to concept classes with a concept distance of 1 from the training dataset (pink lines). The model suddenly acquires the capability to compositionally generalize to a concept class with a concept distance of 2 from the training dataset (dark pink line). Figure 4(c) shows the images generated with the model over time. We observe that rough shapes and sizes are learned relatively early in training, by the 4th epoch, while the color is highly biased to be red, the majority color in the training dataset, up to the 10th epoch. Around the 20th epoch, the model then learns to generate the underrepresented.
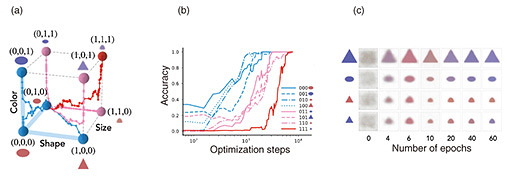
Fig. 4. Concept distance from the training set governs the order in which compositional capabilities emerge. (a) Concept graph (cube) depicting training data points (blue nodes) and concept distances for test data points, where pink nodes represent distance = 1, and dark pink nodes represent distance = 2. Each trajectory represents the learning dynamics of generated images given a tuple prompt. During every training epoch, 50 images are generated, and binary classification is executed to predict each concept, including color, shape, and size. (b) Compositional generalization occurs in sequence, starting with concept distance = 1 and progressing to concept distance = 2. The x-axis represents the number of optimization steps, and the y-axis represents the progress of compositional generalization. (c) Images generated as a function of time clearly show a sudden emergence of the capability to change the color of small, blue, triangles.
3.2 Multiplicative impact of capabilities drives the sudden emergence of compositional generalization
The interpretability of our experimental setup illustrates that the multiplicative reliance on underlying capabilities is the critical structure behind the sudden emergence of compositional generalization in our setup. For example, Fig. 5(a) shows the dynamics of an additive vs. multiplicative accuracy measure for generating concept class {111, (triangle, small, blue)}, which has a concept distance of 2 from the training data. We observe a sudden improvement in the multiplicative measure. To better understand the above, Fig. 5(b), plots the accuracy of probes used for predicting each concept variable (shape, size, color). The model fails to acquire strong color-transformation capabilities until the final stage of training, effectively bottlenecking compositional generalization of 111 class. This empirical observation leads us to the following hypothesis on the emergence of compositional abilities in generative models.
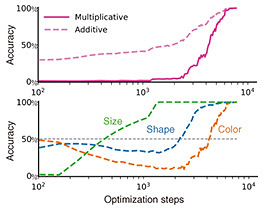
Fig. 5. Multiplicative impact of individual capabilities elicits an °»emergence°… of compositionality. (a) Accuracy of producing samples from the concept class {111, (triangle, blue, small)}, which has a concept distance of 2 from the training data. A multiplicative measure (solid line) has a score of 1 when all concept variables of shape, color, and size are correctly predicted. Conversely, an additive measure (dashed line) independently relates each concept-variable prediction accuracy to the compositional accuracy, deceptively suggesting smooth progress. (b) Learning dynamics of predicting each of the three concept variables: shape (blue), color (orange), and size (green).
4. Ongoing and future directions: Interdisciplinary insights into artificial intelligence behavior
In our artificial intelligence (AI) research group at Harvard and NTT Research, we bridge insights from physics, neuroscience, and psychology, viewing intelligence in AI as an emergent phenomenon, to uncover how AI develops remarkable abilities. In this article, we introduced our recent research [28], where we explored generative AI models through simple and interpretable tasks. We demonstrated how image-generation AI, powered by diffusion models, generates new images by creatively combining previously learned concepts.
We continued exploring through a series of follow-up studies to deepen our insights. In one study [29], we found sudden shifts in the learning trajectory that precisely marked the moments when new, hidden capabilities emerged. Our subsequent study [30] provides theoretical background on this phenomenon in the learning dynamics of diffusion models. In another follow-up study [31], we used ideas from physics, specifically percolation theory, to explain how concepts within Transformer models rapidly connect once enough data is introduced, leading to the emergence of new powerful capabilities.
In collaboration with psychologists and psychiatrists, our ongoing research addresses central questions for the coming years: What cognitive models underlie large language models, and how might these models shape human cognition?
Acknowledgements
We are deeply grateful to Professor Venkatesh Murthy (Harvard Department of Molecular & Cellular Biology) for his invaluable guidance and support throughout this research. Special thanks to Professor Talia Konkle (Harvard Department of Psychology) for her insightful discussions on visual cognition, and to Professor Tomer D. Ullman (Harvard Department of Psychology) for his expertise and feedback on cognitive modeling.
References
| [1] |
P. Dhariwal and A. Nichol, “Diffusion Models Beat GANs on Image Synthesis,” Advances in Neural Information Processing Systems (NeurIPS), Vol. 34, pp. 8780–8794, 2021. |
| [2] |
Z. Pan, X. Zhou, and H. Tian, “Arbitrary Style Guidance for Enhanced Diffusion-based Text-to-image Generation,” Proc. of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), pp. 4461–4471, 2023.
https://doi.org/10.1109/WACV56688.2023.00444 |
| [3] |
J. Ho, A. Jain, and P. Abbeel, “Denoising Diffusion Probabilistic Models,” Advances in Neural Information Processing Systems (NeurIPS), Vol. 33, pp. 6840–6851, 2020. |
| [4] |
J. Ho, W. Chan, C. Saharia, J. Whang, R. Gao, A. Gritsenko, D. P. Kingma, B. Poole, M. Norouzi, D. J. Fleet, and T. Salimans, “Imagen Video: High Definition Video Generation with Diffusion Models,” arXiv preprint arXiv:2210.02303, 2022. |
| [5] |
J. Ho, T. Salimans, A. Gritsenko, W. Chan, M. Norouzi, and D. J. Fleet, “Video Diffusion Models,” Advances in Neural Information Processing Systems (NeurIPS), Vol. 35, pp. 8633–8646, 2022. |
| [6] |
B. Kawar, S. Zada, O. Lang, O. Tov, H. Chang, T. Dekel, I. Mosseri, and M. Irani, “Imagic: Text-based Real Image Editing with Diffusion Models,” Proc. of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 6007–6017, 2023.
https://doi.org/10.1109/CVPR52729.2023.00582 |
| [7] |
C. Saharia, W. Chan, S. Saxena, L. Li, J. Whang, E. Denton, S. K. Seyed Ghasemipour, B. Karagol Ayan, S. Sara Mahdavi, R. Gontijo-Lopes, T. Salimans, J. Ho, D. J. Fleet, and M. Norouzi, “Photorealistic Text-to-image Diffusion Models with Deep Language Understanding,” Advances in Neural Information Processing Systems (NeurIPS), Vol. 35, pp. 36479–36494, 2022. |
| [8] |
V. Goel, E. Peruzzo, Y. Jiang, D. Xu, N. Sebe, T. Darrell, Z. Wang, and H. Shi, “Pair-Diffusion: Object-level Image Editing with Structure-and-appearance Paired Diffusion Models,” CoRR, 2023. |
| [9] |
Q. Zheng, X. Xia, X. Zou, Y. Dong, S. Wang, Y. Xue, Z. Wang, L. Shen, A. Wang, Y. Li, T. Su, Z. Yang, and J. Tang, “CodeGeeX: A Pre-trained Model for Code Generation with Multilingual Benchmarking on HumanEval-X,” Proc. of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD 2023), pp. 5673–5684, 2023.
https://doi.org/10.1145/3580305.3599790 |
| [10] |
F. Cassano, J. Gouwar, D. Nguyen, S. Nguyen, L. Phipps-Costin, D. Pinckney, M.-H. Yee, Y. Zi, C. J. Anderson, M. Q. Feldman, A. Guha, M. Greenberg, and A. Jangda, “MultiPL-E: A Scalable and Polyglot Approach to Benchmarking Neural Code Generation,” IEEE Transactions on Software Engineering, Vol. 49, No. 7, pp. 3675–3691, 2023.
https://doi.org/10.1109/TSE.2023.3267446 |
| [11] |
S. H. Vemprala, R. Bonatti, A. Bucker, and A. Kapoor, “ChatGPT for Robotics: Design Principles and Model Abilities,” IEEE Access, Vol. 12, pp. 55682–55696, 2024.
https://doi.org/10.1109/ACCESS.2024.3387941 |
| [12] |
Boston Globe, “A Boston Dynamics robot can now be run using ChatGPT. What could go wrong?”, 2023. |
| [13] |
M. Janner, Y. Du, J. B. Tenenbaum, and S. Levine, “Planning with Diffusion for Flexible Behavior Synthesis,” arXiv preprint arXiv:2205.09991, 2022. |
| [14] |
I. Singh, V. Blukis, A. Mousavian, A. Goyal, D. Xu, J. Tremblay, D. Fox, J. Thomason, and A. Garg, “ProgPrompt: Generating Situated Robot Task Plans Using Large Language Models,” Proc. of 2023 IEEE International Conference on Robotics and Automation (ICRA), pp. 11523–11530, 2023.
https://doi.org/10.1109/ICRA48891.2023.10161317 |
| [15] |
C. Chi, Z. Xu, S. Feng, E. Cousineau, Y. Du, B. Burchfiel, R. Tedrake, and S. Song, “Diffusion Policy: Visuomotor Policy Learning via Action Diffusion,” The International Journal of Robotics Research, 2023.
https://doi.org/10.1177/02783649241273668 |
| [16] |
A. Nichol, P. Dhariwal, A. Ramesh, P. Shyam, P. Mishkin, B. McGrew, I. Sutskever, and M. Chen, “GLIDE: Towards Photorealistic Image Generation and Editing with Text-guided Diffusion Models,” arXiv preprint arXiv:2112.10741, 2021. |
| [17] |
D. Zhang, K. Ahuja, Y. Xu, Y. Wang, and A. Courville, “Can Subnetwork Structure Be the Key to Out-of-distribution Generalization?” Proc. of the 38th International Conference on Machine Learning (ICML 2021), pp. 12356–12367, 2021. |
| [18] |
J. N. Kaur, E. Kiciman, and A. Sharma, “Modeling the Data-generating Process Is Necessary for Out-of-distribution Generalization,” arXiv preprint arXiv:2206.07837, 2022. |
| [19] |
G. Marcus, E. Davis, and S. Aaronson, “A Very Preliminary Analysis of DALL-E 2,” arXiv preprint arXiv:2204.13807, 2022. |
| [20] |
C. Conwell and T. Ullman, “A Comprehensive Benchmark of Human-like Relational Reasoning for Text-to-image Foundation Models,” The 11th International Conference on Learning Representations (ICLR 2023) Workshop, Kigali, Rwanda, May 2023. |
| [21] |
T. Gokhale, H. Palangi, B. Nushi, V. Vineet, E. Horvitz, E. Kamar, C. Baral, and Y. Yang, “Benchmarking Spatial Relationships in Text-to-image Generation,” arXiv preprint arXiv:2212.10015, 2022. |
| [22] |
Y. Du, C. Durkan, R. Strudel, J. B. Tenenbaum, S. Dieleman, R. Fergus, J. Sohl-Dickstein, A. Doucet, and W. Grathwohl, “Reduce, Reuse, Recycle: Compositional Generation with Energy-based Diffusion Models and MCMC,” Proc. of the 40th International Conference on Machine Learning (ICML 2023), pp. 8489–8510, 2023. |
| [23] |
S. Adee, “Reverse Engineering the Brain,” IEEE Spectrum, Vol. 45, No. 6, pp. 51–53, 2008.
https://spectrum.ieee.org/reverse-engineering-the-brain |
| [24] |
H. Tanaka, A. Nayebi, N. Maheswaranathan, L. McIntosh, S. A. Baccus, and S. Gangul, “From Deep Learning to Mechanistic Understanding in Neuroscience: the Structure of Retinal Prediction,” Advances in Neural Information Processing Systems (NeurIPS), Vol. 32, pp. 8537–8547, 2019. |
| [25] |
J. Wei, Y. Tay, R. Bommasani, C. Raffel, B. Zoph, S. Borgeaud, D. Yogatama, M. Bosma, D. Zhou, D. Metzler, E. H. Chi, T. Hashimoto, O. Vinyals, P. Liang, J. Dean, and W. Fedus, “Emergent Abilities of Large Language Models,” arXiv preprint arXiv:2206.07682, 2022. |
| [26] |
S. Arora and A. Goyal, “A Theory for Emergence of Complex Skills in Language Models,” arXiv preprint arXiv:2307.15936, 2023. |
| [27] |
R. Bommasani, D. A. Hudson, E. Adeli, R. Altman, S. Arora, S. von Arx, M. S. Bernstein, J. Bohg, A. Bosselut, E. Brunskill, E. Brynjolfsson, S. Buch, D. Card, R. Castellon, N. Chatterji, A. Chen, K. Creel, J. Quincy Davis, D. Demszky, C. Donahue, M. Doumbouya, E. Durmus, S. Ermon, J. Etchemendy, K. Ethayarajh, L. Fei-Fei, C. Finn, T. Gale, L. Gillespie, K. Goel, N. Goodman, S. Grossman, N. Guha, T. Hashimoto, P. Henderson, J. Hewitt, D. E. Ho, J. Hong, K. Hsu, J. Huang, T. Icard, S. Jain, D. Jurafsky, P. Kalluri, S. Karamcheti, G. Keeling, F. Khani, O. Khattab, P. W. Koh, M. Krass, R. Krishna, R. Kuditipudi, A. Kumar, F. Ladhak, M. Lee, T. Lee, J. Leskovec, I. Levent, X. L. Li, X. Li, T. Ma, A. Malik, C. D. Manning, S. Mirchandani, E. Mitchell, Z. Munyikwa, S. Nair, A. Narayan, D. Narayanan, B. Newman, A. Nie, J. C. Niebles, H. Nilforoshan, J. Nyarko, G. Ogut, L. Orr, I. Papadimitriou, J. S. Park, C. Piech, E. Portelance, C. Potts, A. Raghunathan, R. Reich, H. Ren, F. Rong, Y. Roohani, C. Ruiz, J. Ryan, C. Ré, D. Sadigh, S. Sagawa, K. Santhanam, A. Shih, K. Srinivasan, A. Tamkin, R. Taori, A. W. Thomas, F. Tramèr, R. E. Wang, W. Wang, B. Wu, J. Wu, Y. Wu, S. M. Xie, M. Yasunaga, J. You, M. Zaharia, M. Zhang, T. Zhang, X. Zhang, Y. Zhang, L. Zheng, K. Zhou, and P. Liang, “On the Opportunities and Risks of Foundation Models,” arXiv preprint arXiv:2108.07258, 2021. |
| [28] |
M. Okawa, E. S. Lubana, R. Dick, and H. Tanaka, “Compositional Abilities Emerge Multiplicatively: Exploring Diffusion Models on a Synthetic Task,” Advances in Neural Information Processing Systems (NeurIPS), Vol. 36, pp. 50173–50195, 2023. |
| [29] |
C. F. Park, M. Okawa, A. Lee, H. Tanaka, and E. S. Lubana, “Emergence of Hidden Capabilities: Exploring Learning Dynamics in Concept Space,” Advances in Neural Information Processing Systems (NeurIPS), Vol. 37 pp. 84698–84729, 2024. |
| [30] |
Y. Yang, C. F. Park, E. S. Lubana, M. Okawa, W. Hu, and H. Tanaka, “Dynamics of Concept Learning and Compositional Generalization,” The 13th International Conference on Learning Representations (ICLR 2025), Singapore, Singapore, Apr. 2025. |
| [31] |
E. S. Lubana, K. Kawaguchi, R. P. Dick, and H. Tanaka, “A Percolation Model of Emergence: Analyzing Transformers Trained on a Formal Language,” The 13th International Conference on Learning Representations (ICLR 2025), Singapore, Singapore, Apr. 2025. |
 |
- Maya Okawa
- Research Scientist, Physics & Informatics Laboratories, NTT Research, Inc. / Associate Researcher, Harvard University.
She received a Ph.D. in computer science from Kyoto University in 2022 and M.S. in physics from the University of Tokyo in 2014. She began her career at NTT Human Informatics Laboratories in 2014, later transitioning to NTT Research’s PHI Lab in 2023, where she currently serves as a research scientist in collaboration with Harvard University. Her recent research focuses on analyzing the behaviors of generative AI and developing cognitive models to better understand interactions between users and generative AI models. She received the DBSJ Kambayashi Young Researcher Award in 2020 and the Telecommunications Advancement Foundation Award in 2019.
|
 |
- Hidenori Tanaka
- Group Leader and Senior Research Scientist, Physics & Informatics Laboratories, NTT Research, Inc.
He received a B.S. in physics from Kyoto University in 2014 and M.S. and Ph.D. in applied physics from Harvard University in 2018. He began his research career as a Masason postdoctoral fellow at Stanford University, working with Surya Ganguli and Daniel Fisher from 2018 to 2019. He joined NTT Research’s PHI Lab in 2020, where he currently serves as a group leader and senior research scientist. He has also held positions as an associate at Harvard University’s Center for Brain Science since 2022, and as an affiliate at IAIFI (Institute for Artificial Intelligence and Fundamental Interactions) at the Massachusetts Institute of Technology since 2024.
|
↑ TOP
|
















